Определение точных решений уравнений состояния
Определение функции передачи, её нулей и полюсов
Определение напряжения на нагрузке
Определение амплитудного и фазового спектра входного сигнала
Определение выходного сигнала по вещественной характеристике при помощи приближенного метода Гиллемина
Определение напряжения на нагрузке
Навигация
Анализ цепи во временной области различными методами
Анализ цепи во временной области различными методами
22311
знаков
6
таблиц
33
изображения
Содержание 1. Введение
2. Постановка
3. Анализ цепи во временной области методом переменных состояния при постоянных воздействиях
3.1 Составление уравнений состояния цепи.
3.2 Определение точных решений уравнений. Решение уравнений состояния численным методом
4. Анализ цепи операторным методом при апериодическом воздействии.4.1 Определение функции передачи, её нулей и полюсов
4.2 Определение переходной и импульсной функции
4.3 Определение напряжения через нагрузку
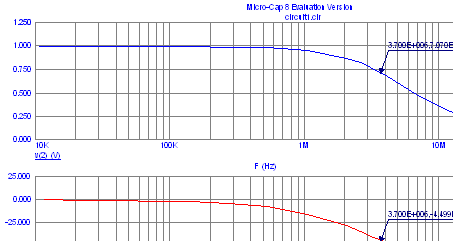
5. Анализ цепи частотным методом при апериодическом воздействии.5.1 Определение амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик функции передачи
5.2 Определение амплитудного и фазового спектра входного сигнала
5.3 Определение амплитудного и фазового спектра выходного сигнала
5.4 Определение выходного сигнала по вещественной характеристике при помощи приближенного метода Гиллемина
6. Анализ цепи частотным методом при периодическом воздействии
6.1 Разложение в ряд Фурье периодической функции и определение её амплитудного и фазового спектров
6.2 Определение напряжения через нагрузку
7. Заключение.
8. Список используемой литературы.
Введение
Практическое применение расчета электрических цепей очень важно. В курсовой работе требуется провести анализ линейной разветвленной электрической цепи различными методами.
Целью курсовой работы является овладение некоторыми современными методами анализа линейной электрической цепи при различных воздействиях в переходном и установившемся режимах с применением вычислительной техники.
В курсовой работе использован следующий материал курса теоретических основ электротехники: методы расчёта сложных цепей, анализ цепей во временной области, операторный метод анализа цепей, частотный метод анализа цепей.
При выполнении курсовой работы применялась программа MathCAD Profession, что позволило значительно упростить вычисления и расчёты в ряде случаев.
2. Постановка задачи
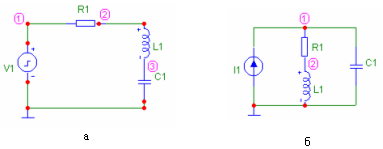
На рисунке 1 представлена анализируемая цепь. Параметры элементов цепи следующие: 
, 
, 
, 
, 
, 
, 
, 
. Здесь 
- единичная ступенчатая функция (функция включения). Параметры одиночного и последовательности импульсов: 
, 
, 
. График одиночного импульса приведён на рисунке 1.1.
 |
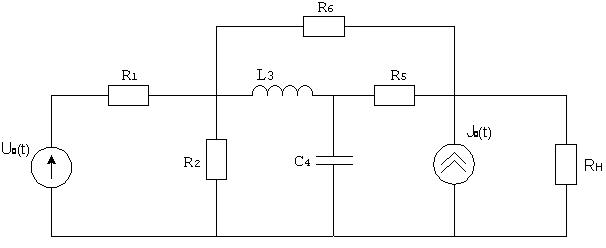Рисунок 1. Схема анализируемой цепи.
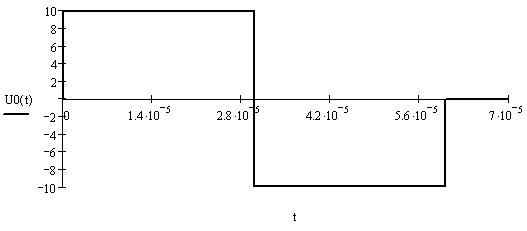
Рисунок 1.1. Входной импульс.
3. Анализ цепи во временной области методом переменных состояния при постоянных воздействиях
3.1 Составление уравнений состояния цепи
Уравнения электромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.
Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники. Количество переменных состояния, следовательно, число уравнений состояния равно числу независимых накопителей энергии.
В данной задаче переменными состояния являются напряжения на ёмкостях и ток в индуктивности: 
и 
. При этом переменные состояния образуют систему из наименьшего числа переменных, полностью определяющих реакции всех ветвей цепи при заданных начальных условиях и приложенных при 
внешних воздействиях.
Требуемая система уравнений может быть получена из системы уравнений, составленной по законам Кирхгофа. При этом целесообразно записывать напряжения и токи на емкости и индуктивности через переменные состояния.
Выберем направления токов (рисунок 2).
 |
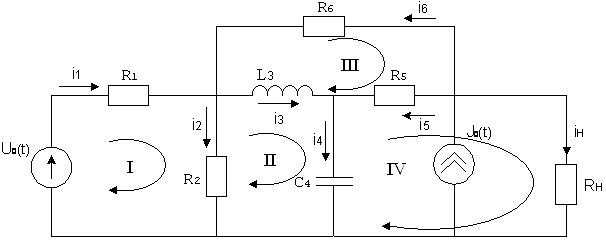Рисунок 2. Выбор направлений токов в ветвях и контуров.
Составим уравнения по законам Кирхгофа:
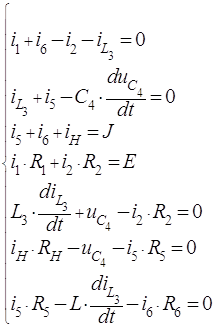
Исключив из уравнений токи и напряжения, не связанные с переменными состояния, получим систему уравнений по методу переменных состояния, разрешенную относительно первых производных (форма Коши):
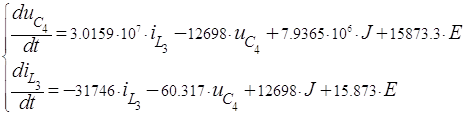(1)
В матричной форме записи эта система имеет вид:
, (2)
где 
матрица коэффициентов при переменных состояния, называемая матрицей Якоби; 
- вектор - столбец переменных состояния; 
- матрица коэффициентов источников тока и э.д.с.; 
- вектор - столбец параметров источников.
В нашем случае это:
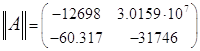
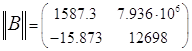
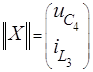
Похожие работы
... отношению к малому сигналу НЭ является линейным, но с переменным параметром (в данном случае крутизной ВАХ). Такой режим работы НЭ называется параметрическим. 1. Аппроксимация характеристик нелинейных элементов При анализе нелинейных цепей (НЦ) обычно не рассматривают процессы, происходящие внутри элементов, составляющих эту цепь, а ограничиваются лишь внешними их характеристиками. Обычно это ...
... , т.е. оплату посредников, трудовых арбитров; организуют работу по урегулированию коллективных трудовых споров. Глава 2. Статистический анализ рынка труда Тюменской области за 1997-2001 г.г. 2.1. Статистические методы анализа рынка труда В статистической практике используются различные методы анализа экономических явлений. Некоторые из них мы рассмотрим в ...
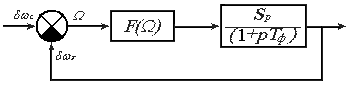
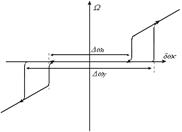
... второго порядков, работающие в условиях действия случайных возмущений, и получить аналитические выражения для этих систем, что является его достоинством. На практике используют комбинацию различных методов. Анализ нелинейного режима работы системы ЧАП Для определения некоторых характеристик системы, произведем качественный анализ системы ЧАП (рис.1) Рис.1. Структурная схема нелинейной ...
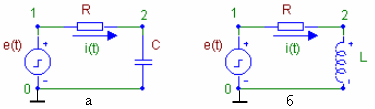
... диода и повторить п. 1.3. Проанализировать полученные результаты. 1.4. Собрать схему, приведенную на рис. 14, подключив к электрической цепи генератор Sine Source. Выбрать модель генератора – GENERAL и задать следующие параметры для моделирования: F = 1 кГц; A = 10 В; DC = 0; PH = 0; RS = 1 Ом; RP = 0; TAU = 0. Рис. 9 Схема рис. 9 представляет собой простейший однопериодный выпрямитель ...
0 комментариев