Определение точных решений уравнений состояния
Определение функции передачи, её нулей и полюсов
Определение напряжения на нагрузке
Определение амплитудного и фазового спектра входного сигнала
Определение выходного сигнала по вещественной характеристике при помощи приближенного метода Гиллемина
Определение напряжения на нагрузке
Навигация
Определение точных решений уравнений состояния
Анализ цепи во временной области различными методами
22311
знаков
6
таблиц
33
изображения
3.2 Определение точных решений уравнений состояния
Решение системы (1) определяется выражением:
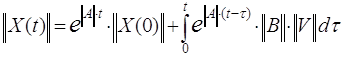
Так как в цепи действуют источники постоянной ЭДС Е и постоянного тока J, то решение может быть представлено в более простом виде:
, (3)
Здесь 
- матричная экспоненциальная функция; 
- вектор-столбец начальных значений переменных состояния; 
- единичная матрица.
Начальные значения переменных состояния могут быть определены из анализа схемы до коммутации. Предполагается, что в схеме до коммутации существовал установившийся режим постоянного тока, что позволяет представить схему в виде:
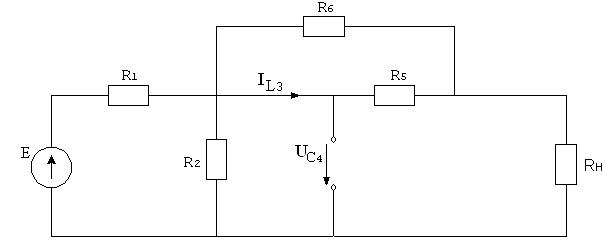
Рисунок 2.1. Схема определения независимых начальных условий.
Анализ схемы рис. 2.1 позволяет определить независимые начальные условия:
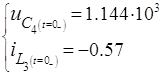(4)
Для определения матричной экспоненциальной функции используем разложение в ряд Тейлора:
, (5)
Число членов разложения должно быть равно числу переменных состояния. 
и 
являются некоторыми функциями времени, которые в свою очередь находятся из системы:
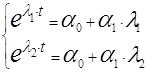(6)
Найдя собственные значения матрицы 
:
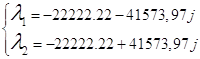
подставляем их в (6) и находим и :
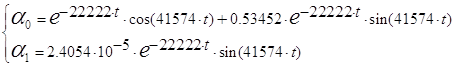
3.3 Решение уравнений состояния численным методом
Решение системы уравнений (1) может быть найдено с помощью какого-либо численного метода интегрирования дифференциальных уравнений. В этих методах интересующий промежуток разбивается на равные малые интервалы h. Приближённые дискретные значения переменных состояния определяются последовательно, на каждом шаге, начиная от времени t = 0.
Решение системы (1) с использованием явного метода Эйлера (или алгоритма Рунге-Кутта первого порядка) имеет вид:
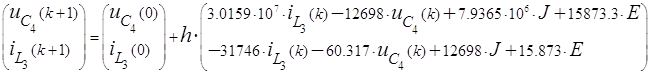Начальным значениям переменных состояния соответствует k = 0. Оценить временной интервал Dtрасч расчета можно на основе известных собственных значений матрицы как Dtрасч = 4/ |lmin|. Здесь |lmin| - минимальное собственное значение, если собственные значения являются вещественными, отрицательными и различными, или вещественная часть комплексного собственного значения, если собственные значения являются комплексно сопряженными. Тогда шаг расчета может быть найден исходя из выражения: h = Dtрасч/N. N - число шагов, на которые разбит интервал Dtрасч. Положим N=80, тогда h = 2,25*10-6. Погрешность расчёта пропорциональна h2 .
Таблица значений переменных состояния на каждом шаге.
Таблица 1.
|
|
|
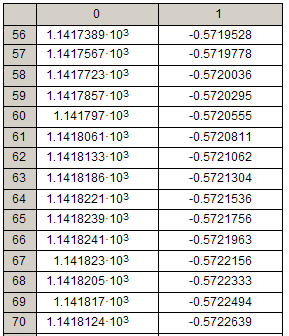
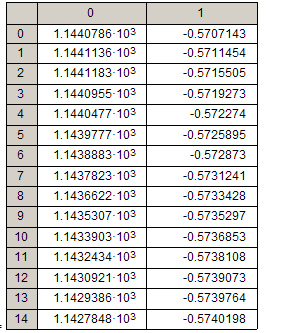U,B I, A
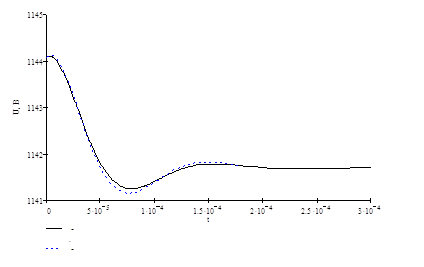
- аналитическое решение
- численное решение
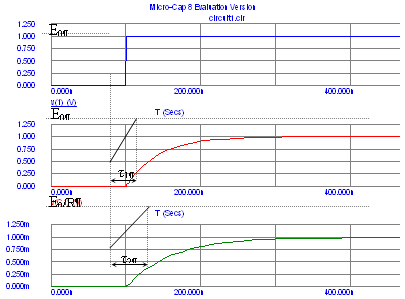
Рисунок 2.2 Изменение напряжения на конденсаторе С4
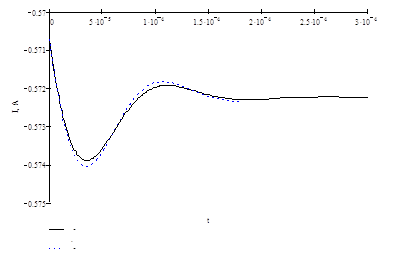
- аналитическое решение
- численное решение
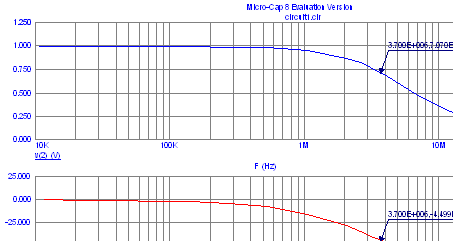
Рисунок 2.3 Изменение тока в катушке индуктивности L3
4. Анализ цепи операторным методом при
апериодическом воздействии
Похожие работы
... отношению к малому сигналу НЭ является линейным, но с переменным параметром (в данном случае крутизной ВАХ). Такой режим работы НЭ называется параметрическим. 1. Аппроксимация характеристик нелинейных элементов При анализе нелинейных цепей (НЦ) обычно не рассматривают процессы, происходящие внутри элементов, составляющих эту цепь, а ограничиваются лишь внешними их характеристиками. Обычно это ...
... , т.е. оплату посредников, трудовых арбитров; организуют работу по урегулированию коллективных трудовых споров. Глава 2. Статистический анализ рынка труда Тюменской области за 1997-2001 г.г. 2.1. Статистические методы анализа рынка труда В статистической практике используются различные методы анализа экономических явлений. Некоторые из них мы рассмотрим в ...
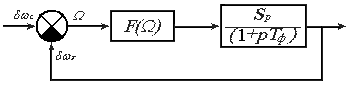
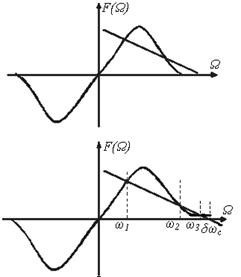
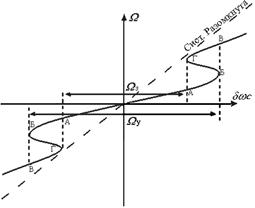
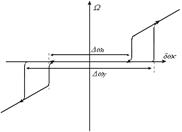
... второго порядков, работающие в условиях действия случайных возмущений, и получить аналитические выражения для этих систем, что является его достоинством. На практике используют комбинацию различных методов. Анализ нелинейного режима работы системы ЧАП Для определения некоторых характеристик системы, произведем качественный анализ системы ЧАП (рис.1) Рис.1. Структурная схема нелинейной ...
... диода и повторить п. 1.3. Проанализировать полученные результаты. 1.4. Собрать схему, приведенную на рис. 14, подключив к электрической цепи генератор Sine Source. Выбрать модель генератора – GENERAL и задать следующие параметры для моделирования: F = 1 кГц; A = 10 В; DC = 0; PH = 0; RS = 1 Ом; RP = 0; TAU = 0. Рис. 9 Схема рис. 9 представляет собой простейший однопериодный выпрямитель ...
0 комментариев