Понятие о конфигурационном пространстве системы частиц

5.0. Понятие о конфигурационном пространстве системы частиц

При описании механических движений в системе частиц с номерами: {1,2, 3, ... n}

могут быть использованы различные пространственные переменные (прямоугольные-декартовы, косоугольные, полярные (шаровые, цилиндрические или эллиптические). Их полная совокупность, достаточная для составления исчерпывающих уравнений механики в конкретной задаче, называется конфигурационным пространством K. Координаты могут быть декартовы {x₁, y₁, z₁, x₂, y₂, z₂, x₃, y₃, z₃, ... x_n, y_n, z_n}, или полярные, например, шаровые {r₁, J₁, j₁, r₂, J₂, j₂, r₃, J₃, j₃, ... r_n, J_n, j_n}, или любые другие - в общем виде: . Максимальная размерность конфигурационного пространства K равна 3n - утроенному числу частиц в системе. Принадлежность переменных к конфигурационному пространству можно указать с помощью символов - кванторов включения, например, в виде: .

5.1. Постулат 1. Волновая функция и её свойства (конечность, однозначность, непрерывность и нормировка).

Формулировка:

Всякое состояние квантово-механической системы описывается функцией со-стояния - волновой функцией, заданной на многообразии всех переменных конфи-гурационного пространства системы, и также времени:

Волновые функции обязаны удовлетворять нескольким математическим требованиям. Они должны быть: 1)конечны, 2)однозначны, 3)непрерывны, 4)нормированны, т.е.:

; (5.1)

 Область интегрирования охватывает весь возможный диапазон значений каждой переменной во всём пространстве K. Вероятностный смысл волновой функции:

 . (5.2)

Нормировка оказывается условием суммирования плотности вероятности во всём конфигурационном пространстве. Квадрат модуля волновой функции является плотностью вероятности, с которой физическая система, пребывая в том физическом состоянии, которое описывается волновой функцией Y, распределена по конфигурационному пространству. Функции, отвечающие условиям 1, 2, 3 называются регулярными.

Волновая функция это математический образ квантово-механического состояния физической системы. Конечно же, это функция механического состояния системы.

5.2. Постулат 2. Измерения физических величин и операторные уравнения на собст-венные значения эрмитовых операторов

Формулировка:

Разрешёнными значениями динамической переменной являются те, что являются собственными значениями эрмитова оператора данной динамической переменной:

 . (5.3)

Операторные уравнения являются математическими образами измерений. Операторы удобно рассматривать в качестве образов макроскопических приборов. Выражения для операторов основных динамических переменных. Оператор импульса и его rомпоненты (из формулы бегущей волны де Бройля). Операторы координат и оператор потенциальной энергии совпадают с самими этими переменными. Взаимосвязь операторов различных динамических переменных определяется тем, что они отображают макроскопическое устройство приборов. Операторы момента импульса одной частицы и его компонент имеют вид , оператор кинетической энергии единственной частицы равен , а для системы нескольких частиц представляет собою сумму вида 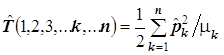. Радиус-вектор частицы , и его оператор представляет собой просто множитель перед волновой функцией, т.е. имеет вид: . Оператор потенциальной энергии это также просто множитель перед волновой функцией U(r)×, оператор полной энергии – гамильтониан складывается из операторов кинетической и потенциальной энергии: . (5.4) Принимается, что и операторы всех прочих динамических переменных построены из этих двух по формулам классической механики.

Причина классической схемы взаимосвязи кроется в том, что операторы являются образами макроскопически устроенных приборов, а конструкционные компоненты которых подчиняются законам классической (макроскопической ) физики.

 Состояния и волновые функции, соответствующие определённым квантованным значениям физически наблюдаемой величины, - тем, которые непосредственно проявляются в измерениях, называются чистыми.