Навигация
8.6. Компоненты лапласиана.
Для сокращения выделим в лапласиане два слагаемых - радиальное и угловое:
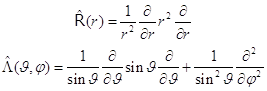(8.4)
Угловой оператор называется оператором Лежандра.
Лапласиан приобретает сжатый вид:
(8.5)
8.7. Угловой оператор (оператор Лежандра)
в свою очередь разделяется далее на два независимых оператора. Один действует на переменную долготы J, второй - на переменную широты j, и получается:
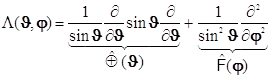
. (8.6)
Операторное уравнение для оператора Лежандра встречается в нескольких очень важных фундаментальных ситуациях. Это задачи: 1) о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) об электронном строении атома H и водородоподобных ионов.
8.8. Уравнение Лапласа для сферической системы:
Уравнением Лапласа называется дифференциальное уравнение в частных производных второго порядка вида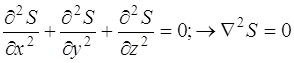 
. В сферических переменных оно имеет вид
. (8.7)
. (8.8)
Решения находятся по методу Фурье: для разделения переменных искомое решение представляется в виде произведения радиальной и угловой компонент функций.
8.9. Разделение переменных.
Общее правило: Если в дифференциальном уравнении в частных производных можно выделить оператор, включающий несколько переменных, и привести его к аддитивной форме, придавая ему вид суммы слагаемых, определённых лишь для отдельных переменных, то исходное дифференциальное уравнение распадается на систему дифференциальных уравнений.
Каждое из них и их решения определены лишь на переменных соответствующего оператора-слагаемого. Частные решения исходного дифференциального уравнения выбираются в мультипликативном виде, как произведения функций – решений отдельных уравнений системы. Этот результат сформулируем в виде краткого правила: «Оператор аддитивен-Решения мультипликативны». Этот подход встречается всюду в теории многоэлектронных систем – атомов и молекул.
8.10. Радиальная часть общего решения сферического уравнения Лапласа выбрана в виде степенной функции от радиальной переменной с показателем степени l принимающим одно из целочисленных неотрицательных значений
. В этом случае соблюдается симметрия общего решения по отношению к взаимным перестановкам декартовых координат, и делается возможно построение регулярных решений (функций класса Q), которые обладают известными свойствами конечности, однозначности и непрерывности, а также могут быть и пронормированы.
.
(8.9)
Угловые сомножители общего решения Y(J,j) называются сферическими гармониками (шаровыми функциями). Запишем уравнение Лапласа, и рассмотрим процедуру разделения переменных:
. (8.10)
Учитывая, что каждый из операторов активен лишь к своим переменным, получаем:
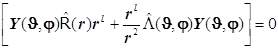. (8.11)
Для разделения переменных следует слева умножить каждое из слагаемых в уравнении на функцию, обратную искомому общему решению. Эта функция равна 
:
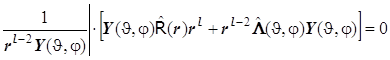
8.11. Получаем равенство, обе части которого содержат независимые переменные и поэтому их обе следует приравнять постоянной величине, т.е.:
. (8.12)
Постоянная легко определяется из радиальной части. Угловая часть уравнения Лапласа представляет собой дифференциальное уравнение Лежандра. Это второе из двух уравнений системы вида
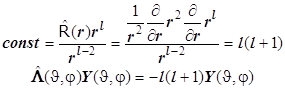. (8.13)
8.12. Уравнение Лежандра
Это операторное уравнение на собственные функции и собственные значения. В квантовой механике таковы все уравнения для динамических переменных. Дифференциальное уравнение Лежандра с точностью до постоянного множителя совпадает с операторным уравнением на собственные значения оператора квадрата момента импульса. Напомним, что оператор момента импульса равен
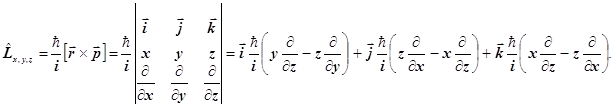
Возводя его в квадрат и вынося влево постоянный множитель, получаем:
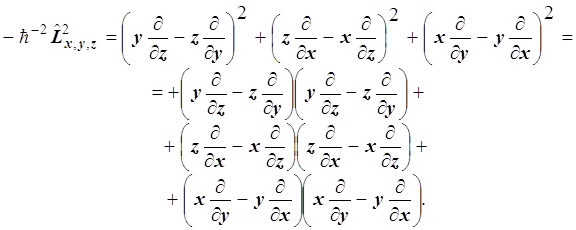
Заменяя декартовы координаты шаровыми и производя всю последовательность действий, находим, что слева получается оператор Лежандра:
. (8.14)
На этом основании решения уравнения Лежандра являются также и решениями операторного уравнения на собственные значения квадрата момента импульса. Так получается строгая формула квантования модуля и проекции момента импульса.
8.13. Квадрат модуля момента импульса определяется собственными значениями оператора Лежандра. Для сравнения представим оба выражения:
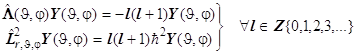. (8.15)
Допустимые значения модуля момента импульса свободно вращающейся вокруг центра масс квантовой системы (ротатора) следуют из операторного уравнения (8.15):
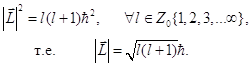. (8.16)
Похожие работы
... 9.2. Водородоподобные орбитали. Многоэлектронный гамильтониан атомной оболочки. Межэлектронное отталкивание как экранирование ядра. Одноэлектронное приближение. Орбитали многоэлектронного атома. 2. Элементы теории многоэлектронных атомов 2.1. Многоэлектронный атом. Содержание. Электронный гамильтониан многоэлектронного атома. Отталкивание электронов, потенциальная энергия отталкивания и ...
... массой, большей урана. В наши дни такие «трансурановые» элементы были получены искусственно. Вполне можно утверждать, что предела таблицы не существует и получение или нахождение других трансурановых элементов – это дело будущего. Таково, в общих чертах, учение об атомах химических элементов, созданное Дальтоном и определившее все дальнейшее развитие химии в XIX столетии. , с помощью ...
... орбиты; 3. Магнитным квантовым числом, характеризующим положение облаков в пространстве; 4. И спиновым квантовым числом, характеризующим веретенообразное движение электрона вокруг своей оси. [ 1, 4 ] Глава II. Строение атома Химики XIXв. Не в состоянии были ответить на вопрос, в чем суть различий между атомами разных элементов, например меди и йода. Лишь в период 1897-1911гг. ...
... этому времени: открытие радиоактивности, экспериментальное доказательство ядерной модели ядра, измерение отношения e / m для электрона, α-частицы и для так называемой H-частицы – ядра атома водорода, открытие искусственной радиоактивности и ядерных реакций, измерение зарядов атомных ядер и т. д. В настоящее время твердо установлено, что атомные ядра различных элементов состоят из двух частиц ...
0 комментариев