Навигация
Уравнение Лежандра содержит две угловые переменные. Их необходимо разделить и исследовать свойства вращения. Раскрывая оператор Лежандра, получаем
16696
знаков
3
таблицы
7
изображений
8.14. Уравнение Лежандра содержит две угловые переменные. Их необходимо разделить и исследовать свойства вращения. Раскрывая оператор Лежандра, получаем
. (8.17)
Шаровые функции представим в виде 
. Их ещё называют сферическими гармониками из-за того, что у них, как и у обычных тригонометрических гармоник – синусоиды и косинусоиды имеются чередующиеся в пространстве пучности и узлы.
Разделим переменные:
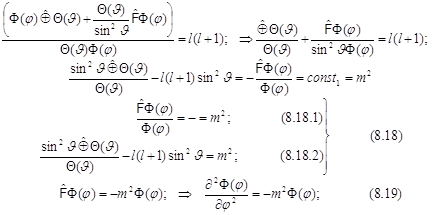
Получена система (8.18) из двух дифференциальных уравнений (8.18.1 и 8.18.2), решения которых связаны общей постоянной.
8.15. Одно из них (8.18.1) имеет знакомый вид. Оно идентично уравнению Шрёдингера для плоского ротатора и описывает свойства вращения относительно оси вращения (вдоль переменной долготы). Полное совпадение с плоским ротатором получится лишь при условии, что в атоме H это уравнение характеризует лишь часть всей ситуации и определяет проекцию момента импульса на ось вращения
Из этого уравнения вытекают значения компоненты момента импульса вдоль оси вращения (в нашем случае – вдоль оси аппликат):
(8.21)
8.16.Второе из уравнений (8.18.2) системы - дифференциальное уравнение для широты:
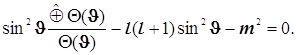(8.22)
Наконец-то обратимся к уравнению Шрёдингера для водородоподобного атома!
8.17. Гамильтониан и уравнение Шрёдингера
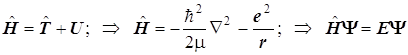. (8.23)
8.17. Несложные преобразования, состоящие только в перемещении и группировке слагаемых, дают следующее:
()
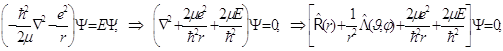
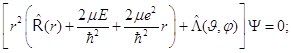Уравнение Шрёдингера для атома водорода приведено к компактному операторному виду, и здесь уже возможно его решение по методу Фурье разделения переменных.
Решения содержат радиальный и угловой сомножители:
8.18. Схема разделения переменных та же, что и в уравнении Лапласа (по правилу «оператор аддитивен - решение мультипликативно». Есть сомножитель радиальный, и есть угловой, и частные решения углового уравнения – сферические функции. Разделим переменные:
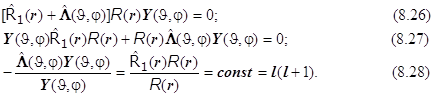
Получается система (8.29) из двух дифференциальных уравнений: (8.29.1) - уравнение Лежандра для сферических гармоник (с точностью до постоянной совпадающее с уравнением для квадрата модуля момента импульса !), и (8.29.2) - чисто радиальное:
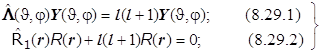. (8.29)8.19. Итоги.
8.19.1. Гамильтониан для электрона в водородоподобном ионе (атоме):
(8.30)
8.19.2. Лапласиан в сферических переменных:
+
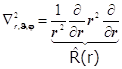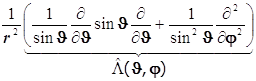
. (8.31)
8.19.3. Уравнение Шрёдингера 
с потенциальной функцией V(r) для одноэлектронных состояний:
. (8.32)
Потенциальная функция V(r) имеет вид:
1) у атома H V(r) = -e2/r,
2) у водородоподобного иона V(r) =-Ze2/r.
Уравнение Шрёдингера в общем виде для водородоподобного иона приобретает вид
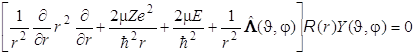. (8.33)
Оно разделяется на систему из трёх дифференциальных уравнений:
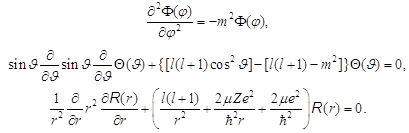. (8.34)
От потенциала зависит лишь радиальная, но не угловая часть уравнения Шрёдингера.
Система этих уравнений даёт полное описание атомных орбиталей - одноэлектронных волновых функций в простейшем случае – в водородоподобном ионе. Первое уравнение совпадает с уравнением Шрёдингера для плоского ротатора, оно описывает свойства вращения вокруг аппликаты (мы выполняли преобразования так, что это ось z). Решения этого уравнения нумеруются квантовым числом
. (8.35)
1) Первое уравнение (как и в плоском ротаторе) описывает компоненту момента импульса вдоль оси вращения, определяя проекцию вектора момента с помощью квантового числа m.
2) Второе и первое уравнения вместе (до разделения угловых переменных) проистекают из одного общего дифференциального уравнения Лежандра
(8.36)
из которого следует правило квантования модуля момента импульса с помощью числа l :
(8.37)
Уравнение (E) предписывает условие
. (8.38)
и возникает следствие 
и магнитное квантовое число m ограничено пределами 
. Всякому квантовому числу l, таким образом, отвечает 2l+1 состояние.
3) Радиальное уравнение приводит к квантованию энергии электронного уровня. Правило квантования одноэлектронных уровней – энергетический спектр водородоподобного иона выражается формулой Бора:
или в атомных единицах:
.
В итоге каждую из атомных орбиталей в атоме водорода можно быть охарактеризовать (пронумеровать) тройкой квантовых чисел 
. Для многих целей, связанных просто с перечислением АО, этих чисел вполне достаточно для их исчерпывающей характеристики, и, поэтому вместо символа волновой функции, достаточно просто перечислить тройку квантовых чисел индексы в скобках или в виде индексов. Этот способ записи эквивалентен волновой функции и такой же точно общий символ АО.
Похожие работы
... 9.2. Водородоподобные орбитали. Многоэлектронный гамильтониан атомной оболочки. Межэлектронное отталкивание как экранирование ядра. Одноэлектронное приближение. Орбитали многоэлектронного атома. 2. Элементы теории многоэлектронных атомов 2.1. Многоэлектронный атом. Содержание. Электронный гамильтониан многоэлектронного атома. Отталкивание электронов, потенциальная энергия отталкивания и ...
... массой, большей урана. В наши дни такие «трансурановые» элементы были получены искусственно. Вполне можно утверждать, что предела таблицы не существует и получение или нахождение других трансурановых элементов – это дело будущего. Таково, в общих чертах, учение об атомах химических элементов, созданное Дальтоном и определившее все дальнейшее развитие химии в XIX столетии. , с помощью ...
... орбиты; 3. Магнитным квантовым числом, характеризующим положение облаков в пространстве; 4. И спиновым квантовым числом, характеризующим веретенообразное движение электрона вокруг своей оси. [ 1, 4 ] Глава II. Строение атома Химики XIXв. Не в состоянии были ответить на вопрос, в чем суть различий между атомами разных элементов, например меди и йода. Лишь в период 1897-1911гг. ...
... этому времени: открытие радиоактивности, экспериментальное доказательство ядерной модели ядра, измерение отношения e / m для электрона, α-частицы и для так называемой H-частицы – ядра атома водорода, открытие искусственной радиоактивности и ядерных реакций, измерение зарядов атомных ядер и т. д. В настоящее время твердо установлено, что атомные ядра различных элементов состоят из двух частиц ...
0 комментариев