Навигация
А > В, Х < У Х – чётное число, У – чётное число
1. А > В, Х < У Х – чётное число, У – чётное число.
Основания и показатели расписываю за один заход.
![]() , где конечно же
, где конечно же ![]() 1>
1>![]() 2,а
2,а ![]() 1 <
1 < ![]() 2.
2.
Вначале разбираемся с показателями
![]()
На второй стадии пройдусь по основаниям
![]()
![]()
Равенство левой и правой части уравнения невозможно.
Тогда и исходное уравнение ![]() решений не имеет.
решений не имеет.
2. А > В, Х < У Х – нечётное число, У – нечётное число.
![]()
Во всех решениях вначале степень, затем основание
![]()
![]()
![]()
Решим полученное условие относительно А и В.
![]()
![]()
![]()
![]()
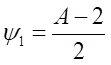
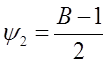
После подстановки А=В+1.
Т.е., чтобы уравнение Ах-Ву=1 существовало при заданных условиях д.б. А=В+1.
3. А > В, Х < У Х – чётное число, У – нечётное число.
![]()
![]()
![]()
Далее вывод, как и в примере (1).
4. А > В, Х < У Х – нечётное число, У – чётное число.
![]()
![]()
![]()
Результат, как и в примере (2).
5. А < В, Х > У Х – чётное число, У – чётное число.
![]()
![]()
Нет решения, ибо это формула разности квадратов.
6. А < В, Х > У Х – нечётное число, У – нечётное число.
![]()
![]()
![]()
![]()
Решение у такой формулы возможно.
7. А < В, Х > У Х – чётное число, У – нечётное число.
![]()
![]()
![]()
Противоречий для существования данной формулы нет.
8. А < В, Х > У Х – нечётное число, У – чётное число.
![]()
![]()
И окончательно.
![]()
Запрета на существование такого уравнения не вижу, но дальнейший анализ не в этой статье.
Вариант II.
9. А > В, Х < У Х – чётное число, У – чётное число.
![]()
![]()
Уравнение разности квадратов - тогда решений не существует.
10. А > В, Х < У Х – нечётное число, У – нечётное число.
![]()
![]()
![]()
Уравнение реальное - тогда решение есть.
11. А > В, Х < У Х – чётное число, У – нечётное число.
![]()
![]()
Уравнение реальное.
Пример: 32-23=1
12. А > В, Х < У Х – нечётное число, У – чётное число.
![]()
![]()
Решение существует.
13. А < В, Х > У Х – чётное число, У – чётное число.
![]()
![]()
14. А < В, Х > У Х – нечётное число, У – нечётное число.
![]()
![]()
15. А < В, Х > У Х – чётное число, У – нечётное число.
![]()
![]()
16. А < В, Х > У Х – нечётное число, У – чётное число.
![]()
![]() (а)
(а)
Для случаев 13, 14, 15, 16 итоговое уравнение одинаковое.
Рассмотрим эти четыре случая чуть подробнее.
![]()
![]() , тогда
, тогда
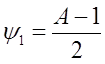
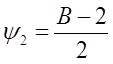
После подставим в уравнение (а) получим
![]() , при начальном условии
, при начальном условии ![]() .
.
Тогда варианты 13, 14, 15, 16 – не верны.
Из рассмотренных выше задач, при всех вариантах начальных условий, - 8 задач решений в целых числах не имеют.
Для закрепления материала предлагаю рассмотреть два заведомо не имеющих решения уравнения.
Первый пример.
Пусть: А - чётное число.
В - нечётное число.
А > В, Х > У, Х – чётное число, У – нечётное число.
Основное противоречие состоит в условии А > В, Х > У.
![]()
![]() ,
,
что, конечно же, не возможно, т.к. левая часть всегда больше правой.
Второй пример.
Пусть: А - нечётное число.
В - чётное число.
А > В, Х > У, Х – чётное число, У – нечётное число.
![]()
После соответствующих преобразований
![]() ,
,
что, конечно же, не возможно.
Гипотеза Биля (ГБ).
![]() , где А, В, С – взаимно простые числа и Х, У, Z > 2.
, где А, В, С – взаимно простые числа и Х, У, Z > 2.
Рассмотрим 2 варианта:
- I А - чётное число, В - нечётное число, С - нечётное число;
- II А - нечётное число, В - чётное число, С - нечётное число.
Строго говоря, чтобы полностью разобрать ГБ, надо рассмотреть все варианты решения уравнений.
Но дело в том, что новый метод исследования диофантовых уравнений говорит о том, что ГБ не верна, т.е. уравнение при некоторых сочетаниях А, В, С, Х, У, Z может иметь место. По этому будет рассмотрено лишь два примера, которые указывают на возможность решения уравнения.
Вариант I.
а) Пусть А > В > С, и Х < У < Z, и А - чётное число, В - нечётное число, С - нечётное число.
Составим функциональное уравнение.
![]()
Подразумевая систему функциональных уравнений, возьмём к = - ![]() 3
3
![]() (1)
(1)
Возьмём обозначение ![]()
![]()
Уравнение (1) примет вид уравнения Каталана ![]()
И именно из этого и следует наличие решений у уравнения ГБ.
Вариант II.
а) Пусть А > В > С, и Х < У < Z, где Х, У – нечётные числа, А - нечётное число, В - чётное число, С - нечётное число.
Составим функциональное уравнение.
![]()
Решая относительно основания, получим ![]()
Проведу преобразование в показателях
![]()
После упрощения.
![]()
Вполне реальное уравнение, которое должно иметь место.
В настоящей работе представлен сравнительно небольшой анализ. Более серьёзным анализом займусь в зиму 2009-2010 годов.
И приведу один контр пример.
Заведомо противоречивое начальное условие – в примере (а) пусть
Х > У > Z.
Тогда в уравнении Каталана
![]() ,
, ![]()
И тогда не может иметь место знак равенства.
Т.е. задача с заведомо неверными начальными условиями исключается сразу.
Вот почему и есть основание верить в решения в целых числах у уравнения ГБ.
Заключение
Данному алгоритму на момент появления в интернете всего два месяца. Дитё.
Что можно нарешать за два месяца? А больше я себе не могу позволить заниматься не профилирующим предметом в моей трудовой деятельности.
Напоследок хочу коснуться одной практической проблемы при решении Диофантовых уравнений данным методом.
Сколько раз можно «бить» по уравнению, представленным алгоритмом?
Можно по отношению к конкретному уравнению теоретически на единицу меньше, чем число неизвестных в данном уравнении.
Первая стадия – убираем самое меньшее неизвестное. А на второй стадии уже надо знать разницу между оставшимся самым маленьким числом, и предстоящим. Или же не зная этой разницы, вводить параметр.
Почему это происходит?На первой стадии мы наши неизвестные приблизим к началу числовой оси. Если самое наименьшее число чётное, то оно будет находиться на позиции «два», а если не чётное – то на позиции «один».
И чтобы ещё по уравнению пройтись представленным алгоритмом, надо все неизвестные «откатить» от начала числовой оси на несколько шагов. Приведу простейший пример.
Пусть есть уравнение Х3+У3+Z3=6903
И пусть каким - то одним нам известным способом мы узнаём, что Х, У, Z – нечётные и следуют подряд.
![]()
![]()
Сдвигаю неизвестные на «шаг» от начала оси.
![]()
![]()
![]()
![]()
![]()
У=2m+1, при m=6 У=13
Z=2m-1, при m=6 Z=11
![]()
при m=6 Х=15
Данный метод позволяет данные вычисления.
Часть 2
Подход к решению уравнений
![]() (1)
(1)
![]() (2)
(2)
Сейчас данные уравнения, насколько мне известно, решены для n=4.
Т.е. доказано наличие для каждого из уравнений бесконечного количества сочетаний натуральных чисел a, b, c, d удовлетворяющим условиям равенств уравнений (1), (2).
Причём доказательства основаны на компьютерном поиске данных чисел. Нашли компьютерным расчётом для n=4, отлично - теперь сделайте тоже самое для n=5 и т.д., т.к. даже для n=1000 в целом проблема не будет закрыта.
Мне кажется, что есть общий подход к доказательству утверждения о существовании равенств в уравнениях (1), (2) при любых n ® ¥.
Я сомневаюсь, что мои рассуждения сойдут за доказательства, но направление, может быть, окажется верным.
I. ![]()
Разберу одну возможность, - пусть все числа a, b, c, d будут чётными.
А далее буду использовать алгоритм решения Диофантовых уравнений.
Составлю систему уравнений. Бумагу экономить не буду, - распишу подробно.
![]()
![]()
![]()
![]()
![]()
![]()
В этих уравнениях пусть ![]() 1 >
1 > ![]() 3 >
3 > ![]() 4 >
4 > ![]() 2 – очевидное предположение.
2 – очевидное предположение.
Произведу в уравнениях системы сокращения на 2n и члены с ![]() 2 перенесу в правую часть уравнений, а члены с
2 перенесу в правую часть уравнений, а члены с ![]() 3 – в левую.
3 – в левую.
Сокращением же на 2n от чётных значений a, b, c, d уравнения системы переведены в значения всего натурального ряда.
![]()
![]()
![]()
![]()
![]()
![]()
Далее используются формулы разности степеней.
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
![]()
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
![]()
![]() +…..+
+…..+![]() =
=![]()
![]() +…..+
+…..+![]()
Т.к. ![]() ,
,![]() , система (4) примет вид:
, система (4) примет вид:
![]() p
p![]() +…..+
+…..+![]() =f
=f![]() +…..+
+…..+![]()
p![]() +…..+
+…..+![]() = f
= f![]() +…..+
+…..+![]()
p![]() +…..+
+…..+![]() = f
= f ![]() +…..+
+…..+![]()
p![]() +…..+
+…..+![]() = f
= f![]() +…..+
+…..+![]()
p![]() +…..+
+…..+![]() = f
= f![]() +…..+
+…..+![]()
Т.е. у каждого уравнения начальной системы уравнений (3) произведено понижение формы.
Ну и конечно же доказательство надо вести не от n к n-1, а наоборот, - от n=2 поэтапно к n ® ¥.
Уравнение (2) доказывается аналогичным образом.
![]() и т.д.
и т.д.
Мне в вышеизложенное и самому не на все 100% верится.
Поэтому я взываю к коллективному разуму.
Главное сомнение же вот в чём:
В таком разе все уравнения с нечётным числом членов решений в натуральных числах не будут иметь, ну или не так строго, могут не иметь.
Т.к. нет понижения формы у одного из членов уравнения.
Как, например, у уравнения (2) бесконечное число сочетаний натуральных чисел a, b, c, d существует, тогда, как у уравнения
![]() таких сочетаний может и не быть.
таких сочетаний может и не быть.
И без компьютерного расчёта, хотя бы для n=3, не обойтись, и если взять мои утверждения, и очень убедительные контрдоводы кого-либо другого.
Похожие работы
... . Общая теория решения Диофантовых уравнений 1-й степени была создана в 17 веке. К началу 19 века трудами П. Ферма , Дж. Виллса, Л. Эйлера, Ж. Лагранжа и К. Гауса в основном было исследовано Диофантово уравнение вида ax²+bxy+cy²+dx+ey+f=0, где а,b,c,d,e,f- целые числа, то есть общее неоднородное уравнение 2-й степени с двумя неизвестными. Перейдем теперь к одной из самых ...
... ; , т.е. . ; Получили общее решение: , где . Способ 2. Рассмотрим еще один способ нахождения решения ЛДУ с двумя неизвестными, а для этого рассмотрим уравнение вида . Уравнения такого вида называются линейными однородными диофантовыми уравнениями (ЛОДУ). Выражая неизвестную , через неизвестную приходим к . Так как x должен быть целым числом, то, где - произвольное целое число. Значит. ...
... первым. Очередное действие всегда определено однозначно. Именно этой цели служат слова “(cледующий шаг).” Они явно указывают какое действие должно быть выполнено следующим. В силу этого свойства алгоритма, которое называется детерминированность, вычислительный процесс всегда для заданных исходных данных определен однозначно. Таким образом, при одних и тех же исходных данных вычислительный процес ...
... данных по сети. ЗАКЛЮЧЕНИЕ В рамках данного дипломного проектирования перед студентом Малышевым А.А. была поставлена задача: на основе алгоритма RSA для шифрования блоков данных, построить алгоритм и реализовать программный продукт для шифрования потоков данных. В результате выполнения дипломного проектирования был составлен принципиальный алгоритм для решения поставленной задачи. Далее он был ...
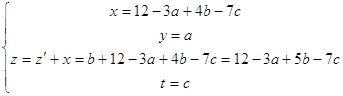
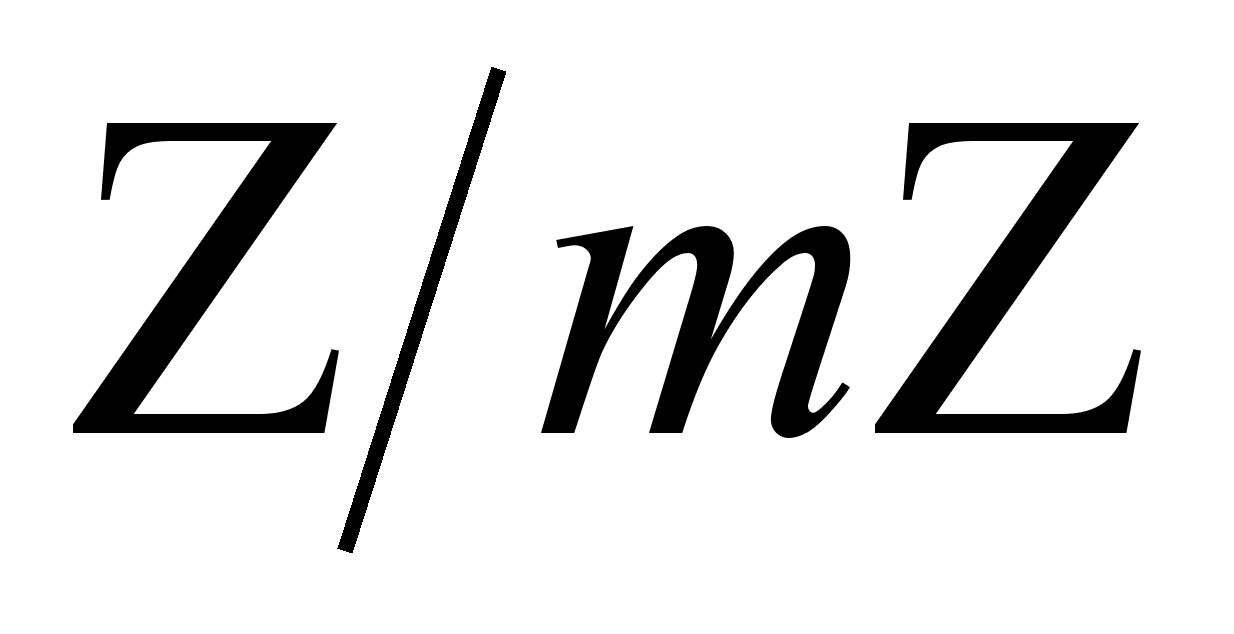
0 комментариев