Навигация
1.1. Задача о ханойской башне
Рассмотрим сначала маленькую изящную головоломку под названием ханойская башня, которую придумал французский математик Эдуард Люка в 1883 г. Башня представляет собой восемь дисков, нанизанных в порядке уменьшения размеров на один из трех колышков. Задача состоит в том, чтобы переместить всю башню на один из других колышков, перенося каждый раз только один диск, и не помещая больший диск на меньший.
Будем решать эту задачу в общем виде, т.е. посмотрим, что будет в случае n дисков.
Будем говорить, что Tn есть минимальное число перекладываний, необходимых для перемещения n дисков с одного колышка на другой по правилам Люка.
Рассмотрим крайние случаи: Т0=0, T1=1, T2=3, T3=7. Эксперимент с тремя дисками дает ключ к общему правилу перемещения n дисков: сначала мы перемещаем (n−1) меньших дисков на любой из колышков (что требует Тn-1 перекладываний), затем перекладываем самый большой диск (одно перекладывание ) и, наконец, помещаем (n−1) меньших дисков обратно на самый большой диск (еще Тn-1 перекладываний). Таким образом, n дисков (при n>0) можно переместить самое большое за 2Tn-1+1 перекладываний (т.е. достаточно перекладываний): Tn≤ 2Tn-1+1.
Сейчас покажем, что необходимо 2Tn-1+1 перекладываний. На некотором этапе мы обязаны переместить самый большой диск. Когда мы это делаем, (n−1) меньших дисков должны находиться на одном колышке, а для того чтобы собрать их вместе, потребуется по меньшей мере Тn-1 перекладываний. Самый большой диск можно перекладывать и более одного раза. Но после перемещения самого большого диска в последний раз мы обязаны поместить (n−1) меньших дисков (которые опять должны находиться на одном колышке) обратно на наибольший диск, что также требует Тn-1 перекладываний. Следовательно, Tn≥ 2Tn-1+1.
Эти два неравенства вместе с тривиальным решением при n=0 дают рекуррентное соотношение:
|
Tn= 2Tn-1+1 при n>0
При достаточно большом n для вычисления Тn потребуется слишком много времени, поэтому получим Тnв простой, компактной, «замкнутой форме», что позволит вычислить Тn быстро.
Первый способ решения (угадывание правильного решения с последующим доказательством, что наша догадка верна).
Вычислим: Т3=2∙3+1=7; Т4=2∙7+1; Т5=2∙15+1; Т6=2∙31+1=63. Теперь можно сделать предположение, что
Тn=2n − 1 при n≥0. (2)
Докажем методом математической индукции по числу n:
1) База: n=0, Т0=20–1=1–1=0 (верно);
2) Индуктивный переход: пусть доказано для всех чисел t ≤ (n–1). Докажем для t=n: Тn= 2Tn-1+1 ![]() 2(2n-1−1)+1 = 2∙2n-1−2+1 = 2n − 1
2(2n-1−1)+1 = 2∙2n-1−2+1 = 2n − 1
Из пунктов 1 и 2 следует: при n≥0 Тn= 2n − 1
Второй способ решения.
К обеим частям соотношения (1) прибавим 1:
Т0+1 = 1,
Тn+1 = 2Tn-1+2 при n>0.
Обозначим Un= Tn+1, тогда получим
U0 = 1
Un= 2Un-1 при n>0.
Решением этой рекурсии есть Un=2n; следовательно Тn = 2n−1.
1.2. Задача о разрезании пиццы
Формулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число Ln областей, на которые плоскость делится n прямыми?
|
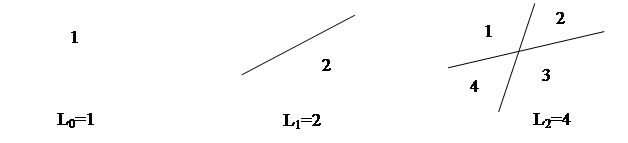
Эксперимент с тремя прямыми показывает, что добавленная третья прямая может рассекать самое большое три старых области вне зависимости от того, как расположены первые две прямые:
 Таким образом, L3=4+3=7 – самое большое, что можно сделать.
Таким образом, L3=4+3=7 – самое большое, что можно сделать.
Обобщая, приходим к следующему выводу: новая n-я прямая (при n>0) увеличивает число областей на k ó когда рассекает k старых областей ó когда пересекает прежние прямые в (k−1) различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать (n−1) старых прямых не более чем в (n−1) различных точках, и мы должны иметь k ≤ n. Установлена верхняя граница:
Ln≤ Ln-1+ n при n>0
В этой формуле можно достичь равенства следующим образом: проводим n-ю прямую так, чтобы она не была параллельна никакой другой прямой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах). Поэтому рекуррентное соотношение имеет вид:
| |
Ln= Ln-1+ n при n > 0
Теперь получим решение в замкнутой форме.
Ln= Ln-1+ n = Ln-2+ (n−1) + n = Ln-3+ (n−2) + (n−1) + n = … = L0+ 1 + 2+ +… + (n−2) + (n−1) + n = 1 + ![]()
Ln = ![]() + 1 при n ≥ 0 (3)
+ 1 при n ≥ 0 (3)
Докажем полученное равенство методом математической индукции.
1) База: n=0, L0=![]() = 1 (верно);
= 1 (верно);
2) Индуктивный переход: пусть доказано для всех чисел t ≤ (n–1). Докажем для t=n:
Ln= Ln-1+ n ![]()
![]() =
= ![]() =
= ![]()
Из пунктов 1 и 2 следует: при n ≥ 0 Ln = ![]() + 1
+ 1
|
 А теперь небольшая вариация на тему прямых на плоскости: предположим, что вместо прямых линий мы используем ломаные линии, каждая из которых представлена одним «зигом». Каково максимальное число Zn областей, на которые плоскость делится n такими ломаными линиями?
А теперь небольшая вариация на тему прямых на плоскости: предположим, что вместо прямых линий мы используем ломаные линии, каждая из которых представлена одним «зигом». Каково максимальное число Zn областей, на которые плоскость делится n такими ломаными линиями? 

|
 Частные случаи:
Частные случаи:  | 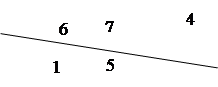 | |||||||
|
| |||||||
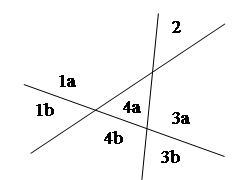
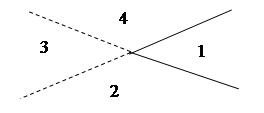
Ломаная линия подобна двум прямым с тем лишь отличием, что области сливаются, если «две» прямые не продолжать после их пересечения:
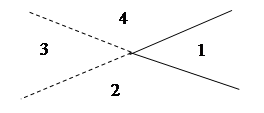 Области 2, 3 и 4, которые были бы разделены при наличии двух прямых, превращаются в единую область в случае одной ломаной линии, т.е. мы теряем две области. И если привести все в надлежащий порядок, то точка излома должна лежать «по ту сторону» пересечений с другими линиями, и мы теряем только две области на одну линию. Таким образом,
Области 2, 3 и 4, которые были бы разделены при наличии двух прямых, превращаются в единую область в случае одной ломаной линии, т.е. мы теряем две области. И если привести все в надлежащий порядок, то точка излома должна лежать «по ту сторону» пересечений с другими линиями, и мы теряем только две области на одну линию. Таким образом,
Zn = L2n− 2n = ![]() = 2n2 −n+1
при n ≥ 0 (4)
= 2n2 −n+1
при n ≥ 0 (4)
Сравнивая решения в замкнутой форме (3) и (4), мы приходим к выводу, что при большом n,
Ln ~ ![]() ,
,
Zn ~ 2n2 ,
так что ломаные линии дают примерно в четыре раза больше областей, чем прямые.
Похожие работы
... то получим из них, путём почленного вычитания: un + 2 - un + 1 = un + 1 - un, или un + 2= 2un + 1 - un (5) - уравнение вида (2). Здесь k = 2, a1 = 2, a2 = -1. Следовательно, арифметическая прогрессия является возвратной последовательностью второго порядка. Пример 3. Рассмотрим старинную задачу Фибоначчи о числе кроликов. В ней требуется определить число пар ...
... достигается при применении автоматизированной формы бухгалтерского учета, использовании персональных компьютеров и прогрессивных программ. 5. Пути совершенствования учета и оценки возвратных отходов Важным условием эффективного использования возвратных отходов на производстве является правильный выбор методов учета. Методология организации бухгалтерского учета материальных ресурсов предполагает ...
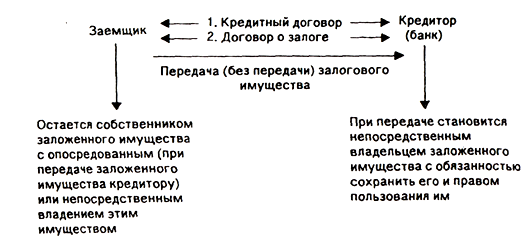
... заложенного имущества. Различают несколько разновидностей залога одним из которых является залог имущества клиента. Залог имущества клиента является одной из распространенных форм обеспечения возвратности банковского кредита. Залог имущества оформляется договором о залоге, подписанным двумя сторонами и подтверждающим право кредитора при неисполнении платежного обязательства заемщиком получить ...
... возврата практически отсутствует, ссуда представляет собой фактически потери банка), 100% резерв от суммы основного долга.3. Проблемы и перспективы развития различных форм обеспечения возвратности кредита 3.1. Выбор формы обеспечения возвратности кредита в зависимости от финансового состояния заемщика. Сфера использования разнообразных форм обеспечения возвратности кредита, учитывая степень ...
0 комментариев