Навигация
1. Задача о ханойской башне
Рассмотрим сначала маленькую изящную головоломку под названием ханойская башня, которую придумал французский математик Эдуард Люка в 1883 г. Башня представляет собой восемь дисков, нанизанных в порядке уменьшения размеров на один из трех колышков. Задача состоит в том, чтобы переместить всю башню на один из других колышков, перенося каждый раз только один диск, и не помещая больший диск на меньший.
Будем решать эту задачу в общем виде, т.е. посмотрим, что будет в случае n дисков.
Будем говорить, что Tn есть минимальное число перекладываний, необходимых для перемещения n дисков с одного колышка на другой по правилам Люка.
Рассмотрим крайние случаи: Т0 = 0, T1 = 1, T2 = 3, T3 = 7. Эксперимент с тремя дисками дает ключ к общему правилу перемещения n дисков: сначала мы перемещаем (n − 1) меньших дисков на любой из колышков (что требует Тn- 1 перекладываний), затем перекладываем самый большой диск (одно перекладывание ) и, наконец, помещаем (n − 1) меньших дисков обратно на самый большой диск (еще Тn- 1 перекладываний). Таким образом, n дисков (при n > 0) можно переместить самое большое за 2Tn – 1 + 1 перекладываний (т.е. достаточно перекладываний):
Tn≤ 2Tn – 1 + 1.
Сейчас покажем, что необходимо 2Tn – 1 + 1 перекладываний. На некотором этапе мы обязаны переместить самый большой диск. Когда мы это делаем, (n − 1) меньших дисков должны находиться на одном колышке, а для того чтобы собрать их вместе, потребуется по меньшей мере Тn- 1 перекладываний. Самый большой диск можно перекладывать и более одного раза.
Но после перемещения самого большого диска в последний раз мы обязаны поместить (n − 1) меньших дисков (которые опять должны находиться на одном колышке) обратно на наибольший диск, что также требует Тn- 1 перекладываний.
Следовательно,
Tn≥ 2Tn – 1 + 1.
Эти два неравенства вместе с тривиальным решением при n = 0 дают рекуррентное соотношение:
Т0 = 0
Tn= 2Tn – 1 + 1 при n > 0 (41)
При достаточно большом n для вычисления Тn потребуется слишком много времени, поэтому получим Тnв простой, компактной, «замкнутой форме», что позволит вычислить Тn быстро.
Первый способ решения (угадывание правильного решения с последующим доказательством, что наша догадка верна). Вычислим:
Т3 = 2∙3 + 1 = 7; Т4 = 2∙7 + 1; Т5 = 2∙15 + 1; Т6 = 2∙31 + 1 = 63.
Теперь можно сделать предположение, что
Тn=2n − 1 при n ≥ 0. (42)
Докажем методом математической индукции по числу n:
1) База: n = 0, Т0=20 – 1 = 1 – 1 = 0 (верно);
2) Индуктивный переход: пусть доказано для всех чисел t ≤ (n – 1). Докажем для
t = n: Тn= 2Tn – 1 +1 ![]() 2(2n – 1 − 1) + 1 = 2∙2n – 1 − 2 + 1 = 2n − 1
2(2n – 1 − 1) + 1 = 2∙2n – 1 − 2 + 1 = 2n − 1
Из пунктов 1 и 2 следует: при n ≥ 0 Тn= 2n − 1
Второй способ решения.
К обеим частям соотношения (41) прибавим 1:
Т0+1 = 1,
Тn+1 = 2Tn – 1 + 2 при n > 0.
Обозначим Un= Tn+ 1, тогда получим
U0 = 1
Un= 2Un- 1 при n > 0.
Решением этой рекурсии есть Un= 2n; следовательно Тn = 2n−1.
2. Задача о разрезании пиццыФормулировка задачи: сколько кусков пиццы можно получить, делая n прямолинейных разрезов ножом? Или, каково максимальное число Ln областей, на которые плоскость делится n прямыми?
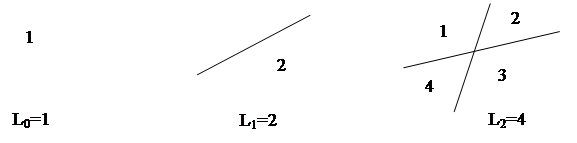
|
Эксперимент с тремя прямыми показывает, что добавленная третья прямая может рассекать самое большое три старых области вне зависимости от того, как расположены первые две прямые:
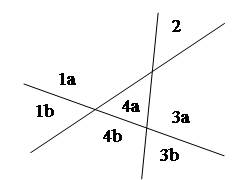 Таким образом, L3 = 4 + 3 = 7 – самое большое, что можно сделать.
Таким образом, L3 = 4 + 3 = 7 – самое большое, что можно сделать.
Обобщая, приходим к следующему выводу: новая n-я прямая (при n > 0) увеличивает число областей на k ó когда рассекает k старых областей ó когда пересекает прежние прямые в (k − 1) различных местах. Две прямые могут пересекаться не более чем в одной точке. Поэтому новая прямая может пересекать (n − 1) старых прямых не более чем в (n − 1) различных точках, и мы должны иметь k ≤ n. Установлена верхняя граница:
Ln≤ Ln – 1 + n при n > 0
В этой формуле можно достичь равенства следующим образом: проводим n-ю прямую так, чтобы она не была параллельна никакой другой прямой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся точек пересечения (следовательно, она пересекает каждую из прямых в различных местах). Поэтому рекуррентное соотношение имеет вид:
| |
Ln= Ln- 1+ n при n > 0
Теперь получим решение в замкнутой форме.
Ln= Ln – 1 + n = Ln – 2 + (n−1) + n = Ln- 3+ (n−2) + (n−1) + n = … = L0+ 1 + 2+ +… + (n−2) + (n−1) + n = 1 + ![]()
Ln = ![]() + 1 при n ≥ 0 (43)
+ 1 при n ≥ 0 (43)
Докажем полученное равенство методом математической индукции.
1) База: n=0, L0=![]() = 1 (верно);
= 1 (верно);
2) Индуктивный переход: пусть доказано для всех чисел t ≤ (n–1). Докажем для t=n:
Ln= Ln-1+ n ![]()
![]() =
= ![]() =
= ![]()
Из пунктов 1 и 2 следует: при n ≥ 0
Ln = ![]() + 1
+ 1
|
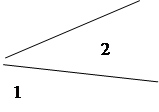
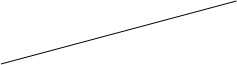 А теперь небольшая вариация на тему прямых на плоскости: предположим, что вместо прямых линий мы используем ломаные линии, каждая из которых представлена одним «зигом». Каково максимальное число Zn областей, на которые плоскость делится n такими ломаными линиями?
А теперь небольшая вариация на тему прямых на плоскости: предположим, что вместо прямых линий мы используем ломаные линии, каждая из которых представлена одним «зигом». Каково максимальное число Zn областей, на которые плоскость делится n такими ломаными линиями? Частные случаи:
 | ||||||||
 | ||||||||
|
| |||||||
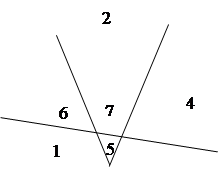
Ломаная линия подобна двум прямым с тем лишь отличием, что области сливаются, если «две» прямые не продолжать после их пересечения:
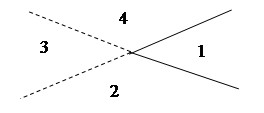 Области 2, 3 и 4, которые были бы разделены при наличии двух прямых, превращаются в единую область в случае одной ломаной линии, т.е. мы теряем две области. И если привести все в надлежащий порядок, то точка излома должна лежать «по ту сторону» пересечений с другими линиями, и мы теряем только две области на одну линию. Таким образом,
Области 2, 3 и 4, которые были бы разделены при наличии двух прямых, превращаются в единую область в случае одной ломаной линии, т.е. мы теряем две области. И если привести все в надлежащий порядок, то точка излома должна лежать «по ту сторону» пересечений с другими линиями, и мы теряем только две области на одну линию. Таким образом,
Zn = L2n− 2n = ![]() = 2n2 −n+1 при n ≥ 0 (44)
= 2n2 −n+1 при n ≥ 0 (44)
Сравнивая решения в замкнутой форме (43) и (44), мы приходим к выводу, что при большом n,
Ln ~ ![]() ,
,
Zn ~ 2n2 ,
так что ломаные линии дают примерно в четыре раза больше областей, чем прямые.
Глава 2 (практическая часть)
1. Рассмотрим последовательность квадратов натуральных чисел:
u1 = 12, u2 = 22, u3 = 32, . . . , un= n2, . . . (*)
Здесь un + 1 = (n + 1)2 = n2 + 2n + 1 и, следовательно,
un + 1 = un+ 2n + 1. (1)
Увеличивая n на единицу, получим:
un + 2 = (n + 2)2 = n2 + 4n + 4 = (n2 + 2n + 1) + 2n + 3 = un + 1+ 2n + 3.
un + 2 = un + 1+ 2n + 3 . (2)
Вычитая почленно (1) из (2), получим:
un + 2 - un + 1= (un + 1+ 2n + 3) – (un + 1 = un+ 2n + 1 ) = un + 1- un + 2,
un + 2 = 2un + 1- un + 2. (3)
Увеличивая в равенстве (3) n на единицу, будем иметь:
un + 3 = (n + 3)2 = n2 + 6n + 9 = (n2 + 4n + 4) + 2n + 5 = un + 2+ 2n + 5,
un + 3 = un + 2+ 2n + 5. (4)
Вычитая почленно (2) из (4), получим:
un + 3 - un + 2 = (un + 2+ 2n + 5) – (un + 1+ 2n + 3 ) = un + 2- un + 1 + 2,
un + 3 = 2un + 2- un + 1 + 2, (5)
Вычитая почленно (3) из (5), получим:
un + 3 - un + 2= (2un + 2- un + 1 + 2) – (2un + 1- un + 2) = 2un + 2- 3un + 1 + un ,
или un + 3 = 3un + 2- 3un + 1 + un.. (6)
Получили возвратное уравнение третьего порядка, т. е. k = 3, a1 = 3, a2 = -3, a3 = 1.
Следовательно, последовательность (*) есть возвратная последовательность третьего порядка.
2. Рассмотрим последовательность кубов натуральных чисел:
u1 = 13, u2 = 23, u3 = 33, . . . , un= n3, . . . (**)
Здесь un + 1 = (n + 1)3 = n3 + 3n2 + 3n + 1 и, следовательно,
un + 1 = un+ 3n2 + 3n + 1. (7)
Увеличивая n на единицу, получим:
un + 2 = (n + 2)3 = n3 + 6n2 + 12n + 8 = (n3 + 3n2 + 3n + 1) + 3n2 + 9n + 7 = = un + 1+ 3n2 + 9n + 7,
un + 2 = un + 1+ 3n2 + 9n + 7. (8)
Вычитая почленно (7) из (8), получим:
un + 2 - un + 1= (un + 1+ 3n2 + 9n + 7) – (un+ 3n2 + 3n + 1) = un + 1- un + 6n + 6,
un + 2 = 2un + 1- un + 6n + 6. (9)
Увеличивая в равенстве (9) n на единицу, будем иметь:
un + 3 = (n + 3)3 = n3 + 9n2 + 27n + 27 = (n3 + 6n2 + 12n + 8) + 3n2 + 15n + 19= un + 2+ 3n2 + 15n + 19,
un + 3 = un + 2+ 3n2 + 15n + 19. (10)
Вычитая почленно (8) из (10), получим:
un + 3 - un + 2 = (un + 2+ 3n2 + 15n + 19) – (un + 1+ 3n2 + 9n + 7) = un + 2- un + 1 + 6n + 12,
un + 3 = 2un + 2- un + 1 + 6n + 12. (11)
Вычитая почленно (9) из (11), получим:
un + 3 - un + 2= (2un + 2- un + 1 + 6n + 12) – (2un + 1- un + 6n + 6) = 2un + 2- 3un + 1 + un + 6,
или un + 3 = 3un + 2- 3un + 1 + un + 6. (12)
Увеличивая в равенстве (12) n на единицу, будем иметь:
un + 4 = (n + 4)3 = n3 + 12n2 + 48n + 64 = (n3 + 9n2 + 27n + 27) + 3n2 + 21n + + 37 = un + 3+ 3n2 + 21n + 37,
un + 4 = un + 3+ 3n2 + 21n + 37. (13)
Вычитая почленно (10) из (13), получим:
un + 4 - un + 3 = (un + 3+ 3n2 + 21n + 37) – (un + 2+ 3n2 + 15n + 19) = = un + 3- un + 2 + 6n + 18,
un + 4 = 2un + 3- un + 2 + 6n + 18. (14)
Вычитая почленно (11) из (14), получим:
un + 4 - un + 3= (2un + 3- un + 2 + 6n + 18) – (2un + 2- un + 1 + 6n + 12) = = 2un + 3- 3un + 2 + un + 1 + 6,
или un + 4 = 3un + 3- 3un + 2 + un + 1 + 6. (15)
Вычитая почленно (12) из (15), получим:
un + 4 - un + 3= (3un + 3- 3un + 2 + un + 1 + 6) – (3un + 2- 3un + 1 + un + 6) = 3un + 3- 6un + 2 + 4un + 1 - un ,
или un + 4 = 4un + 3- 6un + 2 + 4un + 1 - un . (15)
Получили возвратное уравнение четвёртого порядка, т. е. k = 4, a1 = 4, a2 = -6, a3 = 4, a4 = - 1.
Следовательно, последовательность (**) есть возвратная последовательность четвёртого порядка.
3. Проверим, что условие теоремы:
Для того чтобы система k линейных алгебраических уравнений
![]() Аx1 + Вy1 + . . . + Cz1 = u1
Аx1 + Вy1 + . . . + Cz1 = u1
Аx2 + Вy2 + . . . + Cz2 = u2
. . . . . . . . . . . . . . . . . . . . . (16)
Аxk+ Вyk+ . . . + Czk= uk
с k неизвестными имела решение A, B, . . . , C и притом единственное, при любых значениях правых частей u1, u2, u3, . . . , uk, необходимо и достаточно, чтобы соответствующая ей однородная система
![]() Аx1 + Вy1 + . . . + Cz1 = 0
Аx1 + Вy1 + . . . + Cz1 = 0
Аx2 + Вy2 + . . . + Cz2 = 0
. . . . . . . . . . . . . . . . . . . . . (17)
Аxk+ Вyk+ . . . + Czk= 0
имела бы одно только нулевое решение: A = B = . . . = C = 0 – выполняется в частных случаях
![]() x1 = 0,y1 = 0, . . . , z1 = 0
x1 = 0,y1 = 0, . . . , z1 = 0
x2 = 0,y2 = 0, . . . , z2 = 0 (18)
xk = 0, yk = 0, . . . , zk = 1
![]() x1 = 1,y1 = 1, . . . , z1 = 1
x1 = 1,y1 = 1, . . . , z1 = 1
x2 = 0,y2 = 1, . . . , z2 = 1 (19)
xk = 0, yk = 0, . . . , zk = 1
1) x1 = 0,y1 = 0, . . . , z1 = 0
x2 = 0,y2 = 0, . . . , z2 = 0
xk= 0, yk= 0, . . . , zk= 1
Тогда однородная для (16) система (17) примет вид
А•1 = 0
![]() В•1= 0
В•1= 0
. . . . . .
C•1= 0
![]() А = 0
А = 0
![]() В= 0
В= 0
. . . . . .
C= 0
Т. е. A = B = . . . = C = 0.
Получили, что k линейных алгебраических уравнений (16) с k неизвестными имеет единственное решение
![]() A = B = . . . = C = 0.
A = B = . . . = C = 0.
2) x1 = 1,y1 = 1, . . . , z1 = 1
x2 = 0,y2 = 1, . . . , z2 = 1
xk = 0, yk = 0, . . . , zk = 1
Тогда однородная для (16) система (17) примет вид
![]() А•1+ В•1+ . . . + C•1 = 0
А•1+ В•1+ . . . + C•1 = 0
В•1+ . . . + C•1 = 0
. . . . . . . . . . . . . . . . . . . . .
C•1= 0
Решая эту систему с конца, получим A = B = . . . = C = 0. Получили, что k линейных алгебраических уравнений (16) с k неизвестными имеет единственное решение A = B = . . . = C = 0.
Заключение
В данной работе поставленные цели достигнуты.
В работе изучены основные теоретические сведения о возвратных последовательностях, приведены примеры таких последовательностей, также доказаны некоторые теоремы. Нужно заметить, что часть теоретического материала рассматривается именно через примеры, с помощью которых выводятся основные формулы теории возвратных последовательностей. Также затронута тема «возвратные задачи», в работе подробно разобраны некоторые из них. Третья глава посвящена изучению и применению возвратных последовательностей в школьном курсе математики, что можно включить в учебную программу факультатива по математике в средней школе.
В практической части применены полученные знания теории возвратных последовательностей. А именно: доказано по определению, что последовательности являются возвратными и проверено условие выполнения теоремы в частных случаях.
Тема «Возвратные последовательности» не является изолированной, Она близка к школьному курсу математики (арифметическая и геометрическая прогрессии, последовательности квадратов и кубов натуральных чисел и т.д.), используется в высшей алгебре, геометрии, математическом анализе и других математических дисциплинах. Теория возвратных последовательностей составляет особую главу математической дисциплины, называемой исчислением конечных разностей; представляет собой частную главу о последовательностях.
Таким образом, в данной курсовой работе изучена очень важная и актуальная на сегодняшний день тема.
Список литературы
1. Грехем, Р. Конкретная математика. Основание информатики. / Р. Грехем, Д. Кнут, О. Паташник. Пер. с англ. – М.:Мир, 1998. – С. 17−37.
2. Маркушевич А. И. Возвратные последовательности. Популярные лекции по математике. - М.: Наука, 1950.
3. Мантуров О. В. Математика в понятиях, определениях и терминах. Ч.2 / О. В. Мантуров, Ю. К. Солнцев, Ю. И. Соркин, Н. Г. Федин; Под. ред. Л. В. Сабинина. – М.: Просвещение, 1982. – С. 207–208.
Похожие работы
... тогда ; · n = 5k + 2, тогда ; · n = 5k + 3, тогда ; · n = 5k + 4, тогда . Из пунктов 1 и 2 следует: для n ≥ 5 . Ответ: при всех n ≥ 0 и k, r Z+. Задача 9. Иногда возможно использование «обратной индукции», т.е. доказательства от n к n−1, а не наоборот. К примеру, рассмотрим утверждение P(n): ≤ , если x1,x2,…,xn ≥ ...
... достигается при применении автоматизированной формы бухгалтерского учета, использовании персональных компьютеров и прогрессивных программ. 5. Пути совершенствования учета и оценки возвратных отходов Важным условием эффективного использования возвратных отходов на производстве является правильный выбор методов учета. Методология организации бухгалтерского учета материальных ресурсов предполагает ...
... заложенного имущества. Различают несколько разновидностей залога одним из которых является залог имущества клиента. Залог имущества клиента является одной из распространенных форм обеспечения возвратности банковского кредита. Залог имущества оформляется договором о залоге, подписанным двумя сторонами и подтверждающим право кредитора при неисполнении платежного обязательства заемщиком получить ...
... данного вида лизинга. Однако в силу принципа свободы договора не запрещено заключение непоименованных договоров, хоть и не предусмотренных ГК, но и не противоречащих ему; - при использовании возвратного лизинга налоговое обязательство по своей сути не изменяется, а изменяется объект налогообложения (налогооблагаемая база), однако данное изменение вызвано применением законодательных льгот в ...

0 комментариев