| № | Функция | Преобразование | Графики |
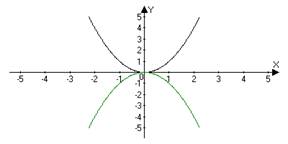
| 1 | y = −ƒ(x) | Сначала строим график функции ƒ(x), а затем симметрично отображаем его относительно оси OX. | y = − (x2) y = x2 → − (x2)
|
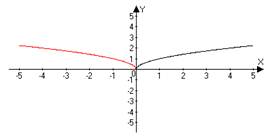
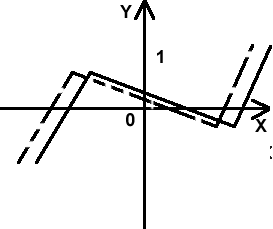
| 2 | y = ƒ(−x) | Сначала строим график функции ƒ(x), а затем симметрично отображаем его относительно оси OY. | y = √ (−x) y =√(x) → √ (−x)
|
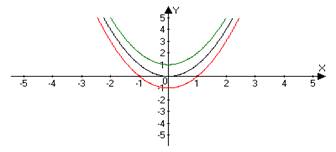
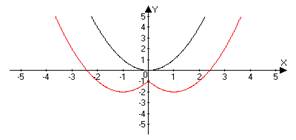
| 3 | y = ƒ(x) +A A - const | Сначала строим график функции ƒ(x), а затем, если А>0 поднимаем полученный график на А единиц вверх по оси OY. Если А<0, то опускаем вниз. | y = x2 → x2 +1 y = x2 → x2 –1
|
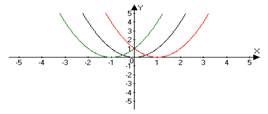
| 4 | y = ƒ(x −а) | Сначала строим график функции ƒ(x), а затем, если а>0, то график функции смещаем на а единиц вправо, а если а<0, то на а единиц влево. "−" − → "+" − ← | y = x2 → (x + 1)2 y = x2→ (x -1)2
|
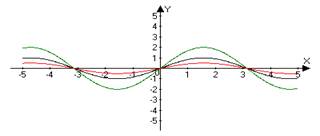
| 5 | y = K ƒ(x ) k − const k>0 | Сначала строим график функции ƒ(x), а затем, если K>0, то растягиваем полученный график в K раз вдоль оси OY. А если 0< K<1, то сжимаем полученный график в 1 ∕ K раз вдоль оси OY. ↕ ↓ ↑ | y = sin(x) → 2sin(x) y = sin(x) → ½ sin(x)
|
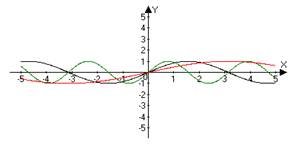
| 6 7 | y = ƒ(к x ) k − const k>0 y = A ƒ(к x+а) +В A, к, а, В − const | Сначала строим график функции ƒ(x), а затем, если к >1, то сжимаем полученный график в к раз вдоль оси OХ. А если 0< к <1, то растягиваем полученный график в 1∕ к раз вдоль оси OХ. к >1 − →← 0< к <1 − ←→ ƒ( x ) → ƒ(к x ) → ƒ(к( х + а ∕ к )) →A ƒ(к( х + а ∕ к )) → A ƒ(к( х + а ∕ к )) +В | y = sin(x) → sin(2x) y = sin(x) → sin (½ x)
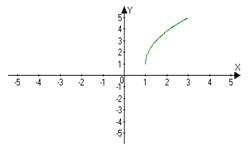
y = 2√(2x-2)+1 y =√x →√2x→√2(x -1) → 2√2(x -1) →2√2(x-1)+1
|
| 8 | y = │ƒ(x)│ | Сначала строим график функции ƒ(x), а затем часть графика, расположенную выше оси ОХ оставляем без изменения, а часть графика, расположенную ниже оси ОХ, заменяем симметричным отображением относительно ОХ. | y =│x3│ y = x3→│x3│
|
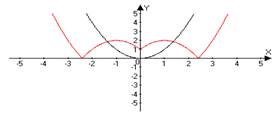
| 9 | y = ƒ(│x│) | Сначала строим график функции ƒ(x), а затем часть графика, расположенную правее оси ОУ, оставляем без изменения, а левую часть графика заменяем симметричным отображением правой относительно ОУ. | y = (│x│−1)2 −2 y = x2→(x -1)2→ (x -1)2 − 2→(│x│−1)2 −2
|
| 10 | y = │ƒ(│x│)│ | ƒ(x) → ƒ(│x│) →│ƒ(│x│)│ | y= │(│x│−1)2 - 2│ y= x2 → (x-1)2 →(x-1)2 - 2→(│x│−1)2 - 2→│(│x│−1)2 - 2│
|
Похожие работы
... работа как прием обучения может входить почти во все методы обучения, воспитывать в учениках потребность самостоятельно добывать знания, умение творчески пользоваться объяснениями учителя, помощью товарищей, книгами, конспектами одна из важнейших целей нашей работы.ГЛАВА 2. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИЙ ПРИЁМЫ И МЕТОДЫ §1. Анализ программ и учебников «Алгебра, 7», «Алгебра, ...
... . 00147-01 9001-1 расширении количества примитивов расширяется список возможных дисциплин, которые могут быть заложены в систему. Разрабатываемая система предназначается для дисциплин "Компьютерная графика" и "Системы искусственного интеллекта", а также для близких с ними дисциплин. Использование одного и того же набора примитивов для создания курсов по указанным дисциплинам приведет к ...
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
... (вопросы а) и в)). Понятие функции, в системе формирования которого должны присутствовать такие задания, сразу выступает в курсе математики как определённая математическая модель, что и является мотивировкой для его углублённого изучения. Методика введения понятий: функции, аргумента, области определения. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его ...

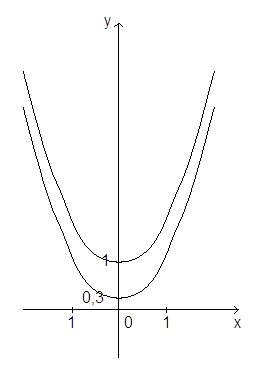
0 комментариев