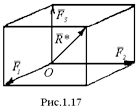
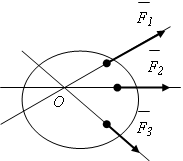
Предположим, что к твердому телу в точках А, В, С, Д приложены силы F1, F2, F3, F4, линии действия которых пересекаются в точке О (рис.1.16а). Перенесем силы вдоль их линий действия в точку О и найдем их равнодействующую. Для определения величины и направления равнодействующей будем последовательно складывать силы по правилу силового треугольника (рис.1.16, б). Сначала найдем равнодействующую R*1 силы F1 и F2, затем R*2 сил R*1 и F3 и т.д. Получим следующее: R*1 = F1 + F2, R*2 = R*1 + F3 = F1 + F2 + F3, R* = R*2 + F4 = F1 + F2 + F3 + F4
Если сил будет n, то
![]() . (1.6)
. (1.6)
Совершив построение, видим, что проведение промежуточных векторов R*1, R*2 было излишним, можно было, отложив вектор F1, к концу его приложить вектор, равный F2, затем к концу F2 - вектор, равный F3, и т.д. Равнодействующая R* соединяет начало первого вектора с концом последнего. Полученная фигура называется силовым многоугольником.
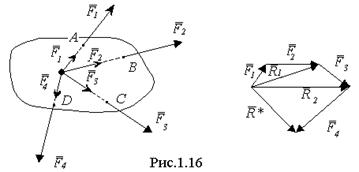
Таким образом, равнодействующая системы сходящихся сил равна геометрической сумме этих сил, линия действия ее проходит через точку пересечения линий действия слагаемых сил. Чтобы найти равнодействующую сходящихся сил геометрическим способом, надо построить в точке пересечений их линий действия силовой многоугольник на слагаемых силах; вектор R*, соединяющий начало первой силы с концом последней (т.е. замыкающая сторона силового многоугольника), является равнодействующей. В частном случае равнодействующая трех сходящихся сил, не лежащих в одной плоскости, изображается диагональю параллелепипеда, построенного на этих силах (правило параллелепипеда). Если силы взаимно перпендикулярны, то параллелепипед будет прямоугольным (рис.1.17). Поскольку сходящаяся система сил может быть заменена одной силой - равнодействующей, то необходимым условием равновесия тела под действием сходящихся сил является равенство нулю этой равнодействующей.
![]() (1.7)
(1.7)
Геометрическое условие равновесия сходящихся сил формулируется так: для равновесия системы сходящихся сил необходимо, чтобы их геометрическая сумма равнялась нулю, т.е. чтобы силовой многоугольник, построенный на слагаемых силах, был замкнут.
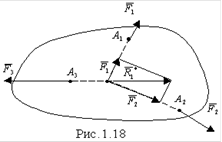
Теорема. Если свободное твердое тело находится в равновесии под действием 3-х непараллельных сил, лежащих в одной плоскости, то линии действия сил пересекаются в одной точке.
Доказательство
Пусть на тело действуют 3 непараллельных силы F1, F2, F3, лежащие в одной плоскости и приложенные в точках А1, А2, А3 (рис.1.18). Так как силы не параллельны, то, по крайней мере, линии действия двух из них пересекаются в одной точке (точка О).
Найдем их равнодействующую R*1:
R*1 = F1 + F2.
Линия действия равнодействующей R*1 пройдет через точку О. Сила R*1 должна уравновешиваться силой F3, а это возможно лишь в том случае (см. аксиому 1), когда они равны по величине и направлены вдоль одной прямой в противоположные стороны. Следовательно, линия действия силы F3 пройдет через точку пересечения линий действия сил F1 и F2, что и требовалось доказать.
Замечание. Три сходящиеся силы, не лежащие в одной плоскости, находиться в равновесии не могут, так как всегда существует их равнодействующая, которая определится как диагональ параллелепипеда, построенного на этих силах.
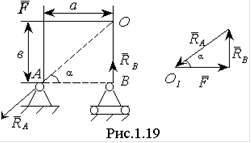
Пример. Определить реакции двухшарнирной арки, если на нее действует сила F. Опора в точке А - шарнирнонеподвижная, а в точке В - шарнирная на катках. Размеры указаны на рис.1.19.
Решение
Линию действия реакции опоры В проводим перпендикулярно к поверхности качения катков. Для определения линии действия реакции опоры А применим теорему о 3-х силах. Так как линии действия сил F и RB пересекаются в точке О, то и линия действия силы RA должна пройти через эту точку. Из точки О1 откладываем силу F, из конца которой проводим линию параллельную RB, а из начала линию параллельную RA, получим силовой треугольник. Направление сил RA и RA показываем, исходя из условия замкнутости силового треугольника.
Находим величины сил:
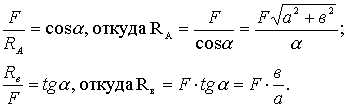
Обновлено 28.07.2009 17: 02
Аналитически определить равнодействующую сходящихся сил можно по проекциям этих сил на неподвижные оси.
Проекция силы на ось, когда сила и ось лежат в одной плоскости (рис.1.20).
Проекцией силы на ось называется скалярная величина, равная взятой со знаком плюс или минус длине отрезка, заключенного между проекциями начала и конца силы на эту ось. Проекция силы на ось имеет знак плюс, если перемещение от ее начала к концу совпадает с положительным направлением оси, и знак минус - если с отрицательным.
Проекция силы на ось (по величине и по знаку) равна произведению модуля силы на косинус угла между направлением силы и положительным направлением оси ![]() . (1.8)
. (1.8)
Из рисунка 1.20 видно, что:
![]()
![]()
На практике рассматривают только острые углы, а знак проекции определяют непосредственно по чертежу. Например, ![]() .
.
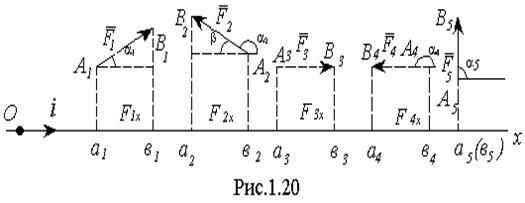
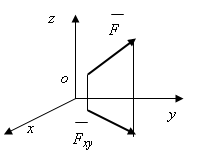
Проекция силы на плоскость. Проекцией силы F на плоскость Оxy называют вектор Fxy, заключенный между проекциями начала и конца силы F на плоскость Оxy (рис.1.21). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная. По модулю Fxy = F cosb где b - угол между направлением силы F и ее проекции Fxy.
Проекция силы на ось, когда сила и ось не лежат в одной плоскости. В этом случае удобнее пользоваться следующим приемом:
а) проецируют силу F на плоскость, содержащую данную ось (например, на ось х-плоскость xOy);
б) найденную проекцию силы на плоскость проецируют на данную ось (ось х). Это и дает искомую проекцию силы на ось. В случае, изображенном на рисунке 1.21, найдем, что:
![]() (1.9)
(1.9)
Этот метод называется методом двойного проецирования.
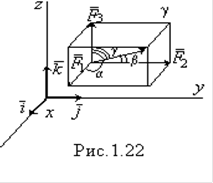
Разложение силы по координатным осям. Операция разложения силы обратна операции сложения сил (см. рис.1.17). Следовательно, чтобы разложить силу F по координатном осям x,y,z, необходимо на силе F, как на диагонали, построить прямоугольный параллелепипед, ребра которого параллельны данным осям x,y,z (рис.1.22)
По формуле диагонали параллелепипеда имеем:
F = F1 + F2 + F3 (1.10)
где F1, F2, F3 - составляющие силы F параллельные осям x.
Если орты осей координат i, j, k то: F1 = iFx, F2 = jFy, F3 = kFz (1.11) где Fx, Fy, Fz - проекции силы F на оси x,y,z. Подcтавляя (1.11) в (1.10), получаем: F = iFx + jFy + kFz. (1.12)
Формула (1.12) называется формулой разложения силы F по координатным осям. Проекции силы на оси координат определяются по формулам:
![]() . (1.13)
. (1.13)
Формула (1.12) справедлива при разложении любого вектора по координатном осям.
Аналитический способ определения силы по ее проекциям на координатные оси x,y,z. Если известны проекции силы на координатные оси x,y,z (риc.1.22), то модуль силы определим по формуле как диагональ прямоугольного параллелепипеда:
![]() , (1.14)
, (1.14)
а ее направление - по трем направляющим косинусам:
![]() . (1.15)
. (1.15)
Аналитический способ определения равнодействующей системы сходящихся сил. Пусть на твердое тело действует сходящаяся система сил (F1, F2,... Fn). В таком случае равнодействующая этой системы сил определяется по формуле (1.6), т.е. равна геометрической сумме данных сил:
![]() .
.
Спроецируем это векторное равенство на оси прямоугольных координат и найдем проекции равнодействующей:
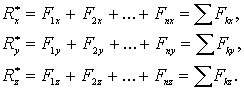 (1.16)
(1.16)
Величина равнодействующей силы определится, согласно формуле (1.14), так:
![]() , (1.17)
, (1.17)
а направление - по трем направляющим косинусам:
![]() . (1.18)
. (1.18)
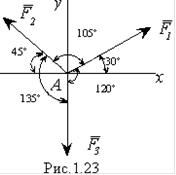
Пример. В точке А к телу приложены три силы: F1=18H, F2=24H, F3=30H, лежащие в одной плоскости и образующие между собой углы 105°,135° и 120°. Определить величину и направление их равнодействующей (рис.1.23)
Решение
Направим ось y по линии действия силы F3, а ось х перпендикулярно к ней. Из рисунка 1.23 видно, что сила F1 образует с положительными направлениями осей углы 30° и 60°, сила F2 - 135° и 45° и сила F3 - 90° и 180°. Пользуясь формулами (1.16) получаем:
![]()
Следовательно, проекции равнодействующей равны:
![]()
Отсюда по формуле (1.17) находим
![]() .
.
Для определения угла a между равнодействующей и осью х имеем:
![]()
Так как и косинус, и синус этого угла отрицательны, то угол лежит в третьей четверти. Находим a= 251,1°.
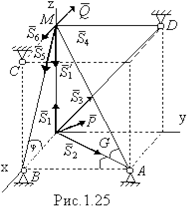
Решение
Сначала рассмотрим равновесие узла L, в котором сходятся стержни 1,2,3. На узел, кроме заданной силы P, действуют еще реакции S1, S2, S3, направленные от узла в предположении, что стержни растянуты. Составляем уравнения равновесия пространственной системы сходящихся сил:
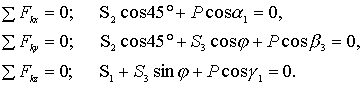
Решив составленные уравнения при заданном значении силы Р и углов, найдем:
S1 = - 172 Н, S2 = - 200 Н, S3 = 83 Н.
Теперь рассмотрим равновесие узла М. На этот узел, кроме силы Q, действуют реакции S4, S5, S6 и S'1. При этом на основании аксиомы взаимодействия реакция S'1 направлена противоположно S1, но численно S'1 = S1 = - 172 Н.
Для узла М уравнения равновесия будут:
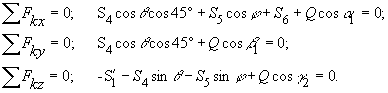
При проецировании силы S4 на оси x и y использовался метод двойного проецирования.
Из последних уравнений находим S4 = - 159Н, S5 = 399Н. S6 = - 179Н.
Отрицательные знаки у S1, S2, S4, S6 указывают, что эти стержни сжаты.
Задача 1.2.1
Равнодействующая плоской системы сходящихся сил F1, F2, F3, F4 равна нулю. Определить модуль силы F1, если известны проекции трех других сил на оси координат:
F2x=4H; F2y=7H; F3x=-5H; F3y=-5H; F4x=-2H; F4y=0. (Ответ: 3,61 Н).
Задача 1.2.2
Известны проекции на оси координат Rx=18H и Ry=24H равнодействующей R плоской системы сходящихся сил F1, F2, F3, а также проекции сил F2, F3 на эти же оси: F2x=-9H; F2y=+7H; F3x=-12H; F3y=0. Определить модуль силы F1. (Ответ: 34,4 Н).
Задача 1.2.3
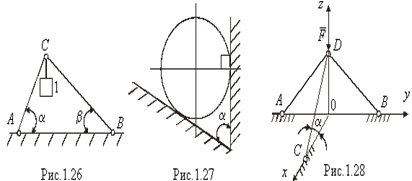
Два невесомых стержня АС и ВС соединены в точке С и шарнирно прикреплены к полу. К шарниру С подвешен груз 1 (рис.1.26). Определить реакцию стержня ВС, если усилие в стержне АС равно 43Н, углы a =60°, b =30°. (Ответ: - 24,8 Н).
Задача 1.2.4
Однородный шар весом 40 Н опирается на две плоскости, пересекающиеся под углом a =60° (рис.1.27). Определить давление шара на наклонную плоскость. (Ответ: 46,2 Н).
Задача 1.2.5
Три стержня AD,BD,CD соединены в точке D шарнирно (рис.1.28). Определить усилие в стержне CD, если сила F=8H находится в плоскости Oyz и угол a =20°. (Ответ: 0).
Равновесие тела под действием плоской системы сил.
Для равновесия твердого тела, находящегося под действием плоской системы сил, необходимо и достаточно, чтобы главный вектор этой системы сил и ее алгебраический главный момент были равны нулю, то есть R = 0, LO = 0, где О - любой центр, расположенный в плоскости действия сил системы.
Вытекающие отсюда аналитические условия равновесия (уравнения равновесия) плоской системы сил можно сформулировать в следующих трех формах:
Основная форма уравнений равновесия:
для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей и сумма их алгебраических моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю:
![]() Fix = 0;
Fix = 0; ![]() Fiy = 0;
Fiy = 0; ![]() MO (Fi) = 0. (I)
MO (Fi) = 0. (I)
Вторая форма уравнений равновесия:
для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех сил относительно двух центров А и В и сумма их проекций на ось Ox, не перпендикулярную оси Ox, были равны нулю:
![]() Fix = 0;
Fix = 0; ![]() MА (Fi) = 0;
MА (Fi) = 0; ![]() MВ (Fi) = 0. (II)
MВ (Fi) = 0. (II)
Третья форма уравнений равновесия (уравнения трех моментов):
для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех сил относительно любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю:
![]() MА (Fi) = 0;
MА (Fi) = 0; ![]() MВ (Fi) = 0;
MВ (Fi) = 0; ![]() MС (Fi) = 0. (III)
MС (Fi) = 0. (III)
Уравнения равновесия в форме (I) считаются основными, так как при их использовании нет никаких ограничений на выбор координатных осей и центра моментов.
С использованием понятия бивектора плоской системы сил условия равновесия в форме (I) могут быть сформулированы следующим образом:
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы бивектор этой системы сил был равен нулю: Wc = ![]() W (Fi) = 0.
W (Fi) = 0.
На этом основании развит матричный метод составления уравнений равновесия плоской системы сил, ориентированный на применение компьютерных систем математических вычислений.
Во всех вышеизложенных формах условия равновесия плоской системы сил выражаются тремя уравнениями.
Задачи статики, в которых число скалярных неизвестных (обычно они представляют собой неизвестные реакции связей) равно числу уравнений равновесия, содержащих эти неизвестные, называются статически определимыми. В этом случае и саму конструкцию (одно твердое тело или систему тел) также называют статически определимой.
Задачи же (а также рассматриваемые конструкции), для которых число неизвестных больше числа уравнений равновесия, называют статически неопределимыми. Такие задачи не могут быть решены с использованием только уравнений равновесия.
Таким образом, чтобы задача статики на равновесие тела под действием произвольной плоской системы сил являлась статически определимой, число неизвестных должно быть равно трем.
Рассмотрим теперь частные случаи плоских систем сил, для которых условия равновесия выражаются двумя уравнениями.
Плоская система параллельных сил.
В этом случае, когда все действующие на тело силы параллельны друг другу, можно для удобства направить ось Ox перпендикулярно силам. Тогда проекция каждой из сил на ось Ох будет равна нулю и первое из уравнений (I) обратится в тождество.
В результате для плоской системы параллельных сил остаются два уравнения равновесия:
![]() Fiy = 0;
Fiy = 0; ![]() MO (Fi) = 0.
MO (Fi) = 0.
Другая форма уравнений для такой системы сил, вытекающая из общих уравнений (II), имеет вид:
![]() MА (Fi) = 0;
MА (Fi) = 0; ![]() MВ (Fi) = 0.
MВ (Fi) = 0.
При этом точки А и В не должны лежать на прямой, параллельной силам.
Плоская система сходящихся сил.
В этом случае, когда линии действия всех сил пересекаются в одной точке, их моменты относительно этой точки равны нулю.
В результате получаем следующие уравнения равновесия:
![]() Fix = 0;
Fix = 0; ![]() Fiy = 0;
Fiy = 0;
то есть для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на координатные оси Ox и Oy были равны нулю.
Задачи статики на равновесие тела под действием плоской системы параллельных или сходящихся сил будут статически определимыми, если в них содержится только две скалярных неизвестных. Подробное изложение матричного метода составления уравнений равновесия твердого тела под действием плоской системы сил, а также примеры и исходные данные для выполнения индивидуальных заданий, дано в учебном пособии (глава 2):
Пример. Определить реакции шарнирных опор А и В балки, находящейся под действием сосредоточенной силы F = 60 Н, равномерно распределенной нагрузки с интенсивностью q = 15 Н/м и пары сил с моментом М = 40 Н · м; расстояние а = 1 м.
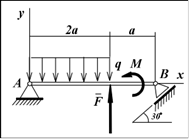
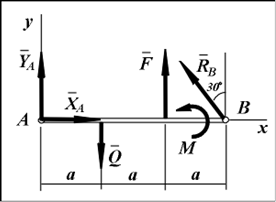
Решение. Введем систему координат Oxy, совместив начало координат О с неподвижным шарниром А и направив осьOx вдоль балки.
Для определения опорных реакций рассмотрим равновесие балки. К ней приложены активные силы: F, пара сил с моментом М и равномерно распределенная нагрузка. Заменим распределенную нагрузку ее равнодействующей Q, равной по модулю Q = q · 2a = 30 Н и приложенной в средней точке участка ее действия.
На балку наложены две связи: неподвижная шарнирная опора в точке А и подвижная шарнирная опора (каток) в точке В. Отбросим мысленно эти связи, заменив их соответствующими реакциями. Реакция RA неизвестна по величине и направлению, поэтому разложим ее на две неизвестные по величине составляющие XA,YA, направленные по координатным осям. Опора в точке В не препятствует ее перемещению вдоль наклонной плоскости и, следовательно, реакцию RB следует направить перпендикулярно наклонной плоскости, то есть эта реакция известна по направлению, но неизвестна по величине.
Таким образом, в задаче имеется три неизвестных скалярных величины: XA, YA, RB. Поскольку для произвольной плоской системы сил имеется три независимых уравнения равновесия, данная задача является статически определимой. Составим уравнения равновесия балки под действием плоской системы сил, содержащей заданные активные силы и неизвестные реакции связей, в форме (II):
![]() Fix = 0;
Fix = 0; ![]() MА (Fi) = 0;
MА (Fi) = 0; ![]() MВ (Fi) = 0.
MВ (Fi) = 0.
Эти уравнения равновесия записываются в рассматриваемом примере следующим образом:
![]() Fix = XA - RB sin 30° = 0; (1)
Fix = XA - RB sin 30° = 0; (1)
![]() MА (Fi) = - Q · a + F · 2a + M + (RB cos 30°) · 3a = 0; (2)
MА (Fi) = - Q · a + F · 2a + M + (RB cos 30°) · 3a = 0; (2)
![]() MВ (Fi) = - YA · 3a + Q · 2a - F · a + M = 0. (3)
MВ (Fi) = - YA · 3a + Q · 2a - F · a + M = 0. (3)
Эта форма уравнений в данном случае обладает тем преимуществом, что каждое из двух уравнений моментов не содержит реакций, приложенных соответственно к моментным точкам А и В (так как их плечи относительно этих точек равны нулю). Напомним, что алгебраические моменты сил берутся со знаком плюс, если они направлены против хода часовой стрелки. При вычислении момента реакции RB относительно точки А выделена ее вертикальна составляющая, равная RB cos 30° и имеющая плечо 3a, а горизонтальная составляющая имеет нулевой момент относительно точки А.
Из уравнений (2) и (3) находим
RB = (Q - 2F - M/a) / (3cos 30°) ![]() -50.0 Н;
-50.0 Н;
YA = (2Q - F + M/a) /3 ![]() 13.3 Н.
13.3 Н.
Полученное отрицательное значение RB означает, что сила RB направлена противоположно тому направлению, которое показано на рисунке.
Для проверки можно составить уравнение проекций сил на ось Oy, которое должно удовлетворяться при найденных значениях YA и RB:
![]() Fiy = YA - Q + F + RB cos 30° = 13.3 - 30 + 60 - 43.3 = 0.
Fiy = YA - Q + F + RB cos 30° = 13.3 - 30 + 60 - 43.3 = 0.
Из уравнения (1) находим
XA = RA sin 30° ![]() -25 Н.
-25 Н.
Знак минус означает, что составляющая XA в действительности направлена в отрицательном направлении оси Ox.
Модуль реакции RA = (XA2 + YA2) ![]()
![]() 28.3 Н.
28.3 Н.
Похожие работы
... и уравнения равновесия системы сходящихся и произвольной систем сил, расположенных в пространстве и в плоскости? 9. Сформулируйте порядок решения задач статики. 2. Кинематика Кинематика- раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как ...
... . Так родился корпускулярно-волновой дуализм с оговоркой, что волновые свойства проявляются только при движении частиц. В качестве объяснения проявления волновых свойств частиц, не противоречащих предложенному “геометрическому” устройству частиц, возможны как минимум два варианта. Первый - “ячеистая” структура вакуума, где частицы могут находиться только в определенных “квантованных” местах ...
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
... В.С. Фарфель и др. Нервная система едина, но условно ее делят на части. Имеется две классификации: по топографическому принципу, т. е. по месту расположения нервной системы в организме человека, и по функциональному принципу, т. е. по областям ее иннервации. По топографическому принципу нервную систему делят на центральную и периферическую. К центральной нервной системе относят головной мозг и ...
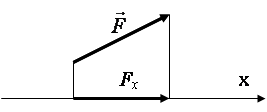


0 комментариев