Деление произвольно заданного угла на 3 равновеликие части. Трисекция угла

Деление произвольно заданного угла на 3 равновеликие части. Трисекция угла

Россия. г. Пенза

Е. И. Терёшкин.

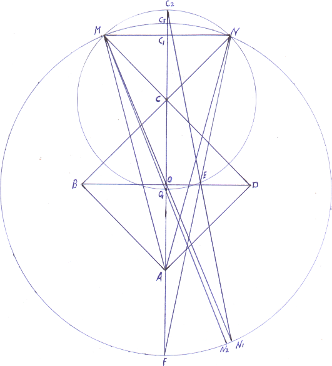
Возьмем прямой угол BAD (чертеж1) достроим его да квадрата ABCD, примем сторону квадрата за 1. Продолжим стороны BC и DC до величины равной . Поставим точки M и N. Соединим точки M и N с точкой A и наш прямой угол BAD разделен на 3 равновеликие части т.е.

Чертеж 1.

Чертеж 2.

Но чтобы делить другие углы надо найти некоторую закономерность. Из точки C радиусом CM опишем окружность.

.

.

.

.

.

По теореме Пифагора находим . Из точки  радиусом опишем окружность. Из точки  через точку  проводим линию до пересечения с большой дугой и ставим точку . , .

.

 - диаметры большого круга. Проводим линию , она пересекает малый круг в точке . Из точки , через точку  проводим линию до пересечения с большой дугой, ставим точку . Соединяем точки  и .

.

.

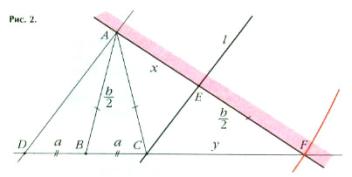
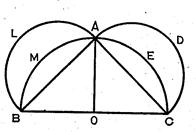
Рассмотрим треугольник  чертеж 2. . По теореме косинусов . Проведем линию  до пересечения с .

По теореме Пифагора  Из точки  проводим линию .  подобен , значит

Рассмотрим , т.к. этот угол вписанный и опирается на диаметр, а  в этом треугольнике будет средняя линия, а значит  По теореме косинусов , значит  но , значит линия  проходит через точку , т.е. через центр квадрата.

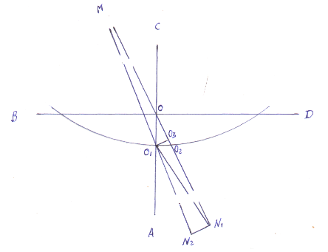
Далее чертим две пересекающиеся прямые, чтобы верхний и нижний вертикальные углы были тупыми (чертеж 3) и острыми (чертеж 4). В местах пересечения ставим точки . Из точек  любым радиусом описываем окружность.

Чертеж 3. Чертеж 4.

Там где стороны верхнего тупого угла (чертеж 3) и острого ( чертеж 4) пересекаются с дугой окружности ставим точки M и N. Проводим биссектрисы обоих тупых углов ( чертеж 3) и острых углов ( чертеж 4). Там где биссектрисы пересекаются с окружностями ставим точки  и . Из точек  радиусом  описываем окружности. Там где биссектрисы пересекаются с нижней точкой окружности ставим точки F. Соединяем точки N с точками F. В местах пересечений линий NF с малой окружностью ставим точки Е. Из точек  через точки Е проводим линии до пересечения с большой дугой и ставим точки . Соединяем точки М с точками . 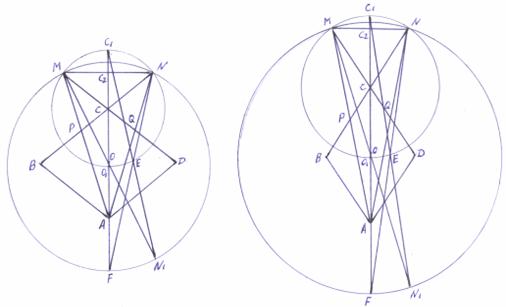В местах пересечений линий М и F ставим точки О. От точек О в сторону точек F по биссектрисам откладываем расстояние СО. Получаем точки А. Из точек А // МС проводим линии до пересечения с продолжениями линий CN и ставим точки В. Из точек А // ВС проводим линии до пересечения с продолжениями линий МС и ставим точки D. Соединяем точки М с точками А и точки N с точками А. Если требуется разделить начальные углы MCN на три равновеликие части, то из точек С направляя вверх проводим линии параллельные AM и AN.

Теперь в местах пересечения АМ и ВС ставим точки Р, а в местах пересечения AN и СD ставим точки Q. Соединяем точки М с точками N. В местах пересечения хорды MN с биссектрисой А ставим точку . Треугольники АМ и АN равны по двум катетам. Треугольники АРС и АСQ равны, т.к.  а АС – общая. Следовательно в обоих чертежах РС=СQ, а ВР=QD и АР=АQ. Далее вынесем оба наших ромба АВСD в отдельные чертежи.

Чертеж 5.

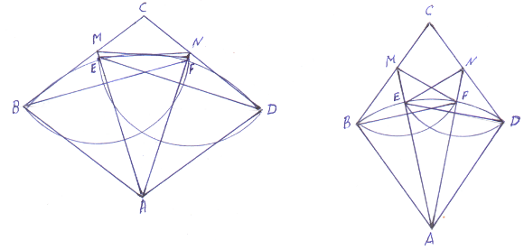
На чертеж 5 (а, б) вынесены ромбы АВСD с тупыми и острыми углами как и на чертежах 3 и 4. Только вместо букв Р и Q применим буквы М и N. Из доказанного ранее известно, что это ромбы, т.е. АВ=ВС=СD=АD, ВМ=ND, и АМ=АN.

Из точек А, радиусом АВ проводим дуги ВD, Из точек М, радиусом ВМ проводим дуги ВF до пересечения с дугами ВD. Из точек N радиусом DN проводим дуги DЕ до пересечения с дугами ВD. Соединяем точки Е с точками N, а точки F с точками М. ВМ=МF=EN=DN. Соединяем точки А с точками Е и F. Проводим хорды BF и ЕD,

Фигуры АВМF состоят из двух равнобедренных треугольников АВF и ВМF имеющих общее основание BF. Значит линии АМ делят эти фигуры на два равных треугольника АВМ и АМF, треугольники равны по трем сторонам.

Фигуры АЕND состоят из двух равнобедренных треугольников АЕD и ЕND, имеющих общее основание ЕD. Значит линии АN делят эти фигуры на два равных треугольника АЕN и АND, треугольники равны по трем сторонам.

Треугольники АВМ равны треугольникам AND по трем сторонам, значит и треугольники АМF равны треугольникам АЕN. Следовательно в обоих чертежах , а и фигуры АВМF равны фигурам AEND каждая в своем чертеже. Но точки Е на линиях АМ могут находиться, а могут и не находиться и точки F на линиях АN могут находиться, а могут и не находиться.

Рассмотрим на обоих чертежах по два четырехугольника: ромбы АВСD и фигуры АЕND. Сумма углов у обоих одинакова.  а  значит  или

В обоих чертежах  равны фигурам АЕND.

.

В результате получается:

или

Рассмотрим в обоих чертежах фигуры АВМF и ромбы АВСD.

или

следовательно

или  Но где находятся точки Е и F пока не известно.

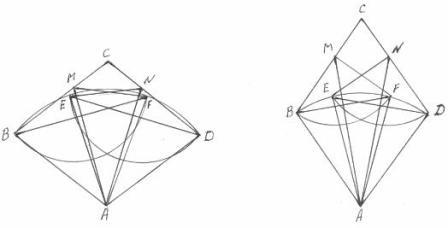
Чертеж 6.

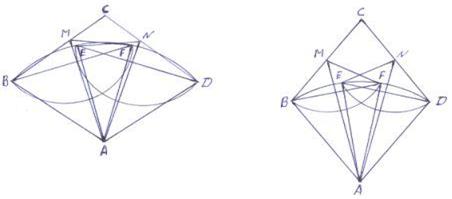
Чертеж 7.

На чертежах 6 (а, б) и 7 (а, б) указанны возможные варианты расположения точек Е и F относительно угла МАN.

Так как углы МАN симметричны относительно биссектрис ромбов АС, потому что,  а , значит точки Е и F если и не находятся на линиях АМ и АN, то находятся на одинаковом расстоянии от этих линий. Иными словами  и , если таковые углы существуют, то эти углы равны между собой. Если  меньше  то  больше  на 2 И наоборот если  больше то меньше  на 2

На чертеже 6 (а, б) рассмотрим (вместе равны фигуре АЕND) и ромб АВСD.

или

На чертеже 7 (а, б) рассмотрим  и ромб АВСD.

Получится, что

Но  и  могут быть равны каким-либо углам, если .

Следовательно, наши углы NAF и EAM = 0, и точка Е находится на линии АМ, а точка F находится на линии AN и .

Угол больше развернутого этот способ не делит на три равновеликие части. Значит, его надо разделить пополам, любую из половинок разделить на три части и взять 2/3. Это и будет 1/3 делимого угла.