Навигация
Преимущества модели АРТ
1. Преимущества модели АРТ
Интересно отметить тот факт, что уравнение АРТ является обобщением уравнения САРМ , хотя арбитражная теория строилась как её альтернатива. Это позволяет утверждать, что модель АРТ – производная от модели САРМ. В сущности, АРТ является ее дополнением и расширением, потому как она описывает зависимость стоимости актива не только от рыночного фактора (стоимости рыночного портфеля), – что, собственно, предполагает однофакторная модель оценки капитальных активов, – но и от других, в том числе нерыночных, факторов риска – курса национальной валюты, стоимости энергоносителей, уровня инфляции и безработицы и т. д.
Таким образом, главным достоинством модели арбитражного ценообразования считается ее многофакторность. Учёт нескольких факторов риска, влияющих на доходность, позволяет исследователю строить более строгую модель. Это дает возможность более точного прогноза изменения цены актива, с одной стороны, а с другой – позволяет уменьшить несистематический риск даже без составления портфеля.
В классической модели САРМ учитывался только один фактор, и актив характеризовался двумя параметрами - коэффициентом чувствительности "бета", характеризующим риск, связанный с этим фактором, и средней остаточной доходностью Е, отвечающей за специфический риск, то есть риск, не объясняющийся влиянием выбранного фактора.
В модели АРТ появилась возможность учитывать несколько факторов. Теперь актив характеризуется набором показателей "бета", каждый из которых представляет собой чувствительность актива к определённому фактору и характеризует систематический риск, связанный с влиянием именно этого фактора, и, по-прежнему, остаточной доходностью Е, только теперь величина специфического (необъяснённого факторами) риска стала гораздо меньше[7].
2. Недостатки теории арбитражного ценообразования
В ходе моделирования арбитражного ценообразования перед исследователем неизбежно встает ряд вопросов, касающихся как теоретических аспектов, непосредственно связанных с формализацией модели, так и практической стороны этого процесса, обусловленной ограниченностью возможностей использования модели арбитражного ценообразования для расчета ставки дисконта в российских условиях.
Проблемы, связанные с формализацией модели
Одним из наиболее существенных недостатков теории арбитражного ценообразования является неопределенность факторов, влияющих на доходность. Следовательно, основной проблемой теоретического этапа АРТ-моделирования является определение факторного подмножества.
Решение данной проблемы предполагает ответы на ряд вопросов:
Сколько и какие факторы войдут в многофакторную модель АРТ?
Данный вопрос актуален при построении не только модели АРТ, но и любой многофакторной модели, описывающей фондовый рынок.
Совершенно ясно, что не всё многообразие доступных для анализа показателей влияют на поведение цены актива. Однако понять, какие именно это факторы и сколько их, не так просто. Строить же модель сразу по всем доступным факторам не конструктивно - незначимые факторы могут значительно искажать любые результаты, полученные с помощью модели.
В исследовательских работах экономистов, посвященных анализу в области ценообразования акций на фондовом рынке, приводятся различные экономические индикаторы в качестве факторов, определяющих факторное подмножество в модели[8].
Действительно, набор факторов, используемых в анализе рынка ценных бумаг, очень широк. Среди них, как правило, выделяют:
![]() макроэкономические показатели (темпы роста и прироста валового внутреннего дохода, уровень инфляции, цены на нефть и другие);
макроэкономические показатели (темпы роста и прироста валового внутреннего дохода, уровень инфляции, цены на нефть и другие);
![]() процентные ставки, разница между процентными ставками;
процентные ставки, разница между процентными ставками;
![]() микроэкономические показатели работы компании (ставка дивидентов, соотношение "цена – доход", соотношение "балансная стоимость – рыночная стоимость");
микроэкономические показатели работы компании (ставка дивидентов, соотношение "цена – доход", соотношение "балансная стоимость – рыночная стоимость");
![]() рыночные показатели ценной бумаги (размер капитализации, изменчивость дохода, ликвидность);
рыночные показатели ценной бумаги (размер капитализации, изменчивость дохода, ликвидность);
![]() принадлежность к отрасли и т. д.
принадлежность к отрасли и т. д.
Однако все эти факторы имеют некоторые общие характеристики. Во-первых, они отражают показатели общей экономической активности (промышленное производство, общие продажи и ВНП). Во-вторых, они отражают инфляцию. В-третьих, они содержат разновидности фактора процентной ставки (либо разность, либо саму ставку).
Таким образом, при определении факторов, влияющих на доходность, инвестор должен исходить из общеэкономических и отраслевых показателей. Следует отметить, что выбор факторов для расчета ставки дисконтирования с помощью модели АРТ индивидуален для каждого предприятия, а значит, факторный набор может быть расширен на микроуровне.
Одинаковы ли факторы риска для разных активов?
Второй вопрос является более тонким, чем первый. И более сложным. Если для решения первой проблемы можно было бы предложить интуитивное решение - отобрать несколько основных макроэкономических или отраслевых показателей, влияющих, по интуитивным ощущениям исследователя, на цены акций, то для решения второй проблемы этого сделать нельзя. Ведь поведение каждого актива, вообще говоря, индивидуально. Поэтому состав и количество факторов риска у каждого актива могут быть своими. Из каких соображений одному активу поставить в соответствие один набор факторов, а другому - другой?
Не меняется ли состав и количество факторов риска во времени?
Предположим, что каким-то образом удалось найти состав и количество факторов влияния для конкретного актива. Может ли через определённый интервал времени факторная структура измениться? Наши результаты исследований свидетельствуют о нестационарном характере взаимосвязей на фондовом рынке. Это значит, что модель применима лишь в течение определённого срока, после которого возникает необходимость строить её заново. При этом факторы риска могут быть уже другими.
Могут ли факторы влиять на цену только через определённое время?
В самом вопросе уже заложен ответ на него - конечно, могут. Так, подорожание нефти может сказываться на ценах акций транспортных компаний не сразу, а какое-то время спустя. Если факторов несколько, то у каждого фактора может быть своё характеристическое время. Как найти эти времена?
Как ранжировать компании сразу по нескольким показателям?
Построив модель САРМ для множества активов, для выбора наиболее привлекательных активов была возможность сортировать их по чувствительности, систематическому или несистематическому риску. В многофакторном случае актив характеризуется набором систематических рисков, связанных с каждым фактором. Как анализировать их все?
Итак, построение модели арбитражного ценообразования, используемой для определения стоимости ценных бумаг, сопряжено с субъективным отношением инвестора к влияющим факторам. Поскольку инвестор в своем исследовании самостоятельно определяет круг показателей, по его мнению, тесно связанных с доходностью того или иного актива, и методы их анализа, это обуславливает определенную субъективность получаемой оценки.
Проблемы практического применения методов
АРТ-моделирования
Практические возможности использования модели арбитражного ценообразования для расчета ставки дисконта в российских условиях ограничены по нескольким причинам[9].
Во-первых, это недостаток информации. АРТ требует изучения статистических данных по предприятию и конкурентам, а также динамики экономических показателей. С этой точки зрения использовать ее можно только для компаний, акции которых торгуются на фондовом рынке.
Во-вторых, это отсутствие специальных методик расчета отдельных элементов в рамках модели арбитражного ценообразования, вынуждающее использовать проверенные способы расчета ставки дисконтирования для получения более обоснованных и надежных результатов.
И, в-третьих, сложность расчетов. Учитывая первые два момента, сложность расчетов может сделать использование АРТ попросту нецелесообразным исходя из соотношения затрат труда и качества полученных результатов.
На основании рассмотренных выше достоинств и недостатков теории арбитражного ценообразования можно сделать следующие выводы.
Так, с теоретической точки зрения модель АРТ обладает неоспоримыми преимуществами перед прочими моделями фондового рынка:
![]() Модель АРТ расщепляет факторы риска на составляющие, приближая их к условиям, в которых действует конкретный бизнес;
Модель АРТ расщепляет факторы риска на составляющие, приближая их к условиям, в которых действует конкретный бизнес;
![]() АРТ использует относительно более слабые упрощающие анализ предположения (по сравнению, например, с моделью оценки капитальных активов САРМ).
АРТ использует относительно более слабые упрощающие анализ предположения (по сравнению, например, с моделью оценки капитальных активов САРМ).
Однако у модели АРТ есть и существенные недостатки, которые носят как теоретический, так и практический характер, а именно:
![]() АРТ умалчивает о конкретных систематических факторах, влияющих на риск и доходность;
АРТ умалчивает о конкретных систематических факторах, влияющих на риск и доходность;
![]() АРТ требует тщательной подготовки информации и подробного анализа деятельности предприятия и конкурентов, занимаемой рыночной ниши и макроэкономических условий.
АРТ требует тщательной подготовки информации и подробного анализа деятельности предприятия и конкурентов, занимаемой рыночной ниши и макроэкономических условий.
В конечном счете, построение модели АРТ является крайне трудоемким процессом и требует значительных временных затрат на подготовку исследования (то есть сбор первичных данных) и проведение необходимых расчетов, однако в силу неразвитости российского фондового рынка выполнение всех необходимых процедур в конечном счете не может гарантировать получение реальной картины динамики доходности.
Глава III. АРТ-моделирование: теория и практика
§ 1. Эконометрический подход к моделированию фондового рынка:
от общего к частному
Для выявления экономических взаимосвязей (в частности, зависимостей на фондовом рынке) широко применяется аппарат экономико-статистического моделирования. Необходимость разработки специального математического аппарата для анализа экономических процессов обусловлена спецификой задач, особенностью экономической информации, а возможность применения статистических методов в качестве инструмента анализа – тем, что проявление закономерностей в экономике носит, как правило, статистический характер. Применительно к экономическим и финансовым процессам, статистические методы принято называть эконометрическими.
Рассмотрим основные эконометрические приемы, необходимые для проведения нашего исследования в области оценки стоимости акций.
Проведение эконометрического исследования предполагает осуществление процедур корреляционно-регрессионного анализа[10].
Корреляционный анализ выборочных данных позволяет обнаружить и измерить тесноту статистической связи между переменными, которые рассматриваются как случайные величины. В целях анализа корреляции случайных величин на основе выборки, как правило, определяют выборочные коэффициенты корреляции и проверяют статистические гипотезы о значимости корреляционной связи.
В случае взаимосвязи нескольких случайных величин x 1,x 2, …, xp анализу подвергают корреляционную матрицу. В этом случае выборка представляет из себя матрицу наблюдений Х = ||хij||, i = 1, …, n, j = 1, …, p, где n - объем выборки, p - число рассматриваемых случайных величин, i - индекс наблюдения в выборке, j - индекс переменной, величина хij соответствует i-му наблюдению над j-й переменной.
Элементами корреляционной матрицы выступают линейные парные коэффициенты корреляции, вычисляемые между переменными выборки.
Линейный парный коэффициент корреляции является мерой линейной статистической связи двух случайных величин. Выборочный коэффициент парной корреляции определяют как
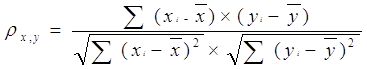 , (2)
, (2)
где i - индекс наблюдения в выборке, i = 1, …, n, n - объем выборки, xi, yi, i = 1, …, n - наблюдения над случайными величинами X и Y соответственно.
Парный коэффициент корреляции характеризует степень приближения статистической связи к линейной. Он отражает взаимосвязь случайных величин и не зависит от того, какая из величин X и Y является причиной, а какая - следствием.
Коэффициент корреляции обладает следующими свойствами:
1). Коэффициент не имеет размерности, следовательно, сопоставим для различных статистических показателей;
2). Величина коэффициента корреляции лежит в пределах от -1 до +1. Значение |ρx,y| = 1 свидетельствует о том, что между переменными существует функциональная зависимость, т. е. все наблюдения лежат на одной прямой (чем ближе |ρx,y| к 1, тем ближе эта связь к функциональной); если ρx,y равен или приближается к нулю, это указывает на отсутствие линейной связи между X и Y, хотя допустимо существование нелинейной зависимости;
3). Если значение ρx,y> 0 (коэффициент корреляции положителен), то взаимосвязь величин прямая: с ростом Х увеличивается Y. Отрицательный коэффициент корреляции говорит об обратной взаимосвязи.
Наличие связи между X и Y может быть обнаружено, если: а) Х есть причина Y; б) Y есть причина Х; в) если Х и Y совместно зависимые величины; г) если Х и Y являются следствием некоторой общей для них причины.
В практике статистического анализа имеют место случаи, когда корреляционный анализ обнаруживает существование достаточно сильной зависимости признаков, в действительности не имеющих причинно-следственной связи между собой, – такие корреляции называют ложными.
Оценка коэффициента корреляции, определенная по выборке, является случайной величиной, поэтому необходимо проверить гипотезу о значимости, т. е. проверить предположение, существенно ли коэффициент корреляции отличается от нуля, или это случайное отклонение, связанное с выборкой. Если ρx,y - коэффициент корреляции в генеральной совокупности, то нулевая гипотеза может быть как:
![]() ,
,
и альтернативная ей
![]() .
.
В качестве критерия применяют статистику, которая для выборки (х, y) из нормальной генеральной совокупности будет иметь t-распределение. Ее вычисляют по формуле:
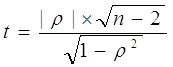 . (3)
. (3)
Расчетное значение критерия сопоставляют с табличным значением распределения Стьюдента t α, ν, где ν - число степеней свободы, ν = n - 2, α - уровень значимости. Если получают t > t α, ν, то нулевая гипотеза отвергается и можно утверждать, что коэффициент корреляции значим. В случае t < t α, ν нет оснований отвергать нулевую гипотезу и следует сделать заключение о том, что коэффициент корреляции незначим[11].
Прикладные цели регрессионного анализа в области экономики заключаются в следующем:
1). Установить наличие статистически значимой регрессионной связи между зависимой и объясняющими переменными;
2). Определить конкретный аналитический вид связи;
3). Спрогнозировать и восстановить значения исследуемого результирующего показателя по известным значениям объясняющих переменных.
Таким образом, построение эконометрической модели является основой любого эконометрического исследования. Она выступает в качестве средства анализа и прогнозирования в различных сферах: финансовой, производственной, инвестиционной, и применяется для исследования объектов самого разного уровня – от отдельных предприятий, отраслей, регионов до страны в целом.
Регрессионная модель представляет собой один из основных типов эконометрических моделей. Она отражает зависимость случайного результирующего показателя y от одной или нескольких детерминированных объясняющих переменных Х = (x1, x2, …, xp).
Выявление регрессионной зависимости осуществляется на основе анализа данных о наблюдениях за экономическими процессами, которые образуют выборки из генеральной совокупности. При построении эконометрических моделей желательно, чтобы все выборочные распределения используемых показателей соответствовали нормальному закону распределения.
Математическую модель регрессионной зависимости можно записать следующим образом:
![]() , (4)
, (4)
где f(X) представляет собой детерминированную составляющую модели, в которой Х выступает как вектор объясняющих переменных Х=(х 1, х 2, ... , х p);
ε – остаточная компонента (возмущение модели).
Детерминированная составляющая модели f(X) выражает влияние существенных факторов на зависимый показатель y и описывает условное математическое ожидание:
![]() . (5)
. (5)
Случайная составляющая отражает суммарное влияние всех несущественных факторов.
В данном случае нас интересует множественная линейная регрессия стоимости ценных бумаг от различных экономических факторов.
Множественной регрессией называют модель, которая включает несколько предсказывающих или объясняющих переменных. Она полнее объясняет поведение зависимой переменной и позволяет сопоставить влияние включенных в уравнение регрессии факторов.
Если регрессия – линейная, то это означает, что факторные признаки линейно влияют на поведение исследуемого показателя.
В общем виде модель множественной линейной регрессии, включающая p объясняющих переменных х 1, ..., хp имеет вид:
![]() , (6)
, (6)
где β 0, β 1, ..., β p – неизвестные оцениваемые параметры регрессии;
х 1, х 2, …, хp - влияющие факторы; ε – остаточная компонента.
Задача оценивания в данном случае заключается в том, чтобы с помощью метода наименьших квадратов найти такие оценки b0, b1, …,bp, которые минимизировали бы квадраты отклонений наблюдаемых значений зависимой переменной yi от расчетных значений, вычисленных с помощью уравнения регрессии.
Функция, значение которой минимизируют с помощью МНК:
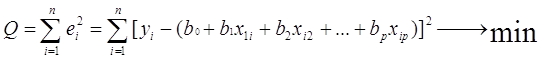 . (7)
. (7)
Оценки параметров регрессии, получаемые по методу наименьших квадратов, обладают статистическими свойствами несмещенности, состоятельности и эффективности.
Свойство несмещенности оценок заключается в том, что оценки параметров bj, найденные с помощью линейного МНК, не содержат систематических ошибок при оценивании. Свойство состоятельности означает, что при росте объема выборки до бесконечности с вероятностью, близкой к единице, можно утверждать, что оценки параметров bj сходятся к оцениваемому параметру βj. Наконец, МНК-оценки являются эффективными, если они характеризуются наименьшей дисперсией в классе линейных оценок.
Чтобы получаемые оценки параметров обладали данными свойствами, необходимо выполнение предпосылок (условий) регрессионного анализа Гаусса-Маркова[12]:
1. Е (ε) = 0, т. е. математическое ожидание остатков равно нулю. Невыполнение данного условия приводит к тому, что оценки параметров теряют свойство несмещенности.
2. Условие гетероскедастичности, или одинакового разброса:
D (ε) = σ2, т. е. дисперсия возмущений в модели распределена равномерно, ее величина постоянна (дисперсия не может увеличиваться с ростом числа наблюдений). Выполнение данного условия позволяет получать эффективные оценки параметров bj.
3. Условие отсутствия автокорреляции: cov (εi, εj) = 0, i, j = 1, …, n, т. е. отдельные наблюдения остаточной компоненты некоррелированы. Оценки метода МНК модели с автокорреляцией случайной составляющей теряют эффективность. Применение МНК в данном случае приводит к существенной недооценке параметров, в связи с чем теряют свое значение процедуры проверки гипотез и обоснованность предсказаний.
4. cov (ε, x j) = 0, j = 1, …, p, т. е. объясняющие переменные не коррелируют с возмущениями модели.
5. ε ![]() N (0, σ2), т. е. случайная составляющая в модели нормально распределена. Нормальность распределения остаточной компоненты гарантирует, что оценки метода МНК будут иметь нормальное распределение.
N (0, σ2), т. е. случайная составляющая в модели нормально распределена. Нормальность распределения остаточной компоненты гарантирует, что оценки метода МНК будут иметь нормальное распределение.
Качество построенного регрессионного уравнения, выступающего в качестве результата проведенного исследования, может быть оценено с помощью ряда показателей, которые можно отнести к группе абсолютных либо относительных.
Среди абсолютных показателей качества наиболее важную роль играют следующие:
1). Средняя ошибка аппроксимации:
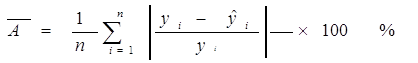 (8)
(8)
Допустимый уровень ошибки – до 10 %.
2). Оценки дисперсий.
– Оценка общей дисперсии:
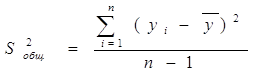 (9)
(9)
Общая дисперсия характеризует разброс значений зависимого признака относительно среднего уровня.
– Оценка объясненной дисперсии:
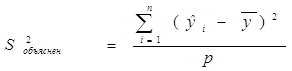 (10)
(10)
Объясненная дисперсия характеризует вариацию зависимого признака, объясненную построенным уравнением регрессии.
– Оценка остаточной дисперсии:
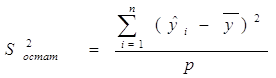 (11)
(11)
Остаточная дисперсия отражает разброс значений относительно линии регрессии (модельных значений) и может служить показателем точности воспроизведения значений зависимой переменной. В случае высокой остаточной дисперсии точность прогнозов результирующего показателя будет невелика и практическое использование построенного уравнения малоэффективным. Напротив, чем меньше остаточная дисперсия, тем больше уверенности в том, что уравнение регрессии подобрано верно.
Большое значение остаточной дисперсии может быть обусловлено неверным выбором функции или отсутствием статистической взаимосвязи между зависимой и объясняющими переменными, включенными в уравнение регрессии.
3). На практике часто используют величину стандартного отклонения от линии регрессии, называемую также стандартной ошибкой регрессии или стандартной ошибкой оценивания:
![]() (12)
(12)
Рассмотренные показатели качества линейной регрессионной модели являются абсолютными, поскольку размер дисперсии напрямую зависит от показателя y.
Среди относительных показателей качества регрессии основным является коэффициент детерминации.
Коэффициент детерминации вычисляют как отношение сумм квадратов:
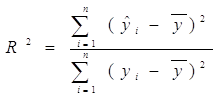 (13) или
(13) или 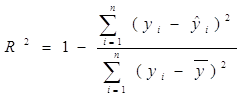 . (14)
. (14)
Коэффициент детерминации показывает долю объясненной уравнением регрессии дисперсии зависимой переменной и выражается в долях.
Коэффициент детерминации изменяется от 0 до 1. Высокое значение R2 говорит о том, что включенные в уравнение регрессии факторы в основном объясняют вариацию значений зависимого признака. Если же значение R2 невелико, то можно сделать вывод о том, что факторы, оказывающие существенное влияние на результирующий показатель, в уравнение регрессии не вошли.
Однако существует ряд ограничений, сужающих возможности применения данного показателя для анализа.
Прежде всего, коэффициент детерминации позволяет проводить сравнение различных линейных по параметрам регрессионных уравнений для одной и той же зависимой переменной.
Второе ограничение связано с количеством объясняющих переменных в модели. Сопоставимые уравнения регрессии зависимой переменной должны включать одинаковое число факторов и могут отличаться лишь составом независимых переменных. Ограничение по количеству объясняющих переменных обусловлено тем, что R2 является неубывающей функцией от числа включенных в регрессию факторов. Поэтому наряду с традиционным часто используют скорректированный коэффициент детерминации, позволяющий проводить сравнение линейных регрессионных уравнений с разным подмножеством факторов:
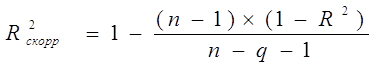 , (15)
, (15)
где R2 - базовый коэффициент детерминации; n - объем выборки; q - число факторов в факторном наборе.
Еще одно требование связано с наличием свободного члена. Константа должна входить или отсутствовать одновременно во всех сравниваемых уравнениях.
Квадратный корень из R2 для линейной модели
![]() (16)
(16)
представляет собой коэффициент множественной корреляции и характеризует тесноту связи совокупности факторов, включенных в уравнение регрессии, с исследуемым показателем.
Кроме того, дополнять оценку качества регрессионного уравнения следует проверкой значимости как параметров регрессии, так и самого регрессионного уравнения.
1). Проверка значимости параметров позволяет установить существенность влияния отдельных факторов на зависимую переменную.
Проверка значимости параметра предполагает проведение процедуры проверки гипотезы о том, что фактор xj не оказывает существенного влияния на зависимую переменную. Нулевую гипотезу относительно параметра модели формулируют следующим образом:
![]() .
.
Альтернативная ей гипотеза утверждает, что βj значимо отличается от нуля:
![]() .
.
Статистика для проверки сформулированной гипотезы принимает вид:
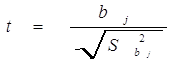 .
(17)
.
(17)
Если верна нулевая гипотеза, то статистика (17) имеет распределение Стьюдента. Расчетное значение t-статистики сравнивают с квантилью t-распределения tα, ν, которая имеет параметры: ν - число степеней свободы,
ν = n-p-1, p - число объясняющих переменных в уравнении регрессии; α - уровень значимости.
Величина α определяет надежность статистических выводов. Чем выше требования к надежности результатов, тем меньше должна быть величина α.
Если расчетное значение t-статистики попадает в критическую для проверяемой гипотезы область | t | > tα, ν, то параметр βj значим, следовательно, фактор xjоказывает существенный вклад в вариацию зависимого признака. В противном случае, если | t | < tα, ν, то влияние фактора несущественно и он может быть исключен из уравнения регрессии.
2). Целью поверки гипотезы о значимости уравнения регрессии является определение существенности влияния на зависимую переменную всех или хотя бы некоторых независимых переменных, включенных в регрессионную модель.
Нулевая гипотеза состоит в том, что все переменные x 1, x 2, …, xp не оказывают существенного влияния на зависимую переменную:
![]() .
.
Альтернативная гипотеза утверждает, что, как минимум, одна из объясняющих переменных оказывает существенное влияние на объясняемую переменную и должна быть включена в регрессионную модель. Гипотеза может быть записана следующим образом:
![]() .
.
Для проверки нулевой гипотезы используют F-критерий:
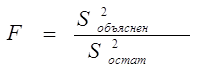 . (18)
. (18)
Если верна нулевая гипотеза, то (18) имеет распределение с числом степеней свободы числителя ν 1 = p и числом степеней свободы знаменателя ν 2 = n - p - 1. Решение о значимости F-критерия принимают, задав некоторый уровень значимости α и определив соответствующую параметрам α, ν 1 и ν 2 квантиль распределения F α, ν 1, ν 2. Если F < F α, ν 1, ν 2, то считают, что нет оснований отвергать нулевую гипотезу, ни одна из включенных в уравнение регрессии переменных не оказывает существенного влияния на y. Напротив, когда F > F α, ν 1, ν 2, то делают заключение, что выборочные данные не подтверждают основную гипотезу, все или некоторые объясняющие переменные существенно влияют на зависимую переменную.
Все рассмотренные показатели качества регрессионного уравнения определяют дальнейшее поведение исследователя: будет он пересматривать построенную модель, внося коррективы в состав факторного набора, или же остановится на достигнутых результатах[13].
§ 2. Теоретическая и практическая реализация АРТ-
моделирования
Как уже было отмечено, построение модели арбитражного ценообразования, используемой для определения стоимости ценных бумаг, сопряжено с субъективным отношением инвестора к влияющим факторам: какие факторы выбрать, каким должен быть критерий включения фактора в модель, – все эти проблемы инвестор решает самостоятельно.
А потому для построения модели арбитражного ценообразования воспользуемся универсальным алгоритмом, предложенным А. А. Шабалиным[14], который, на мой взгляд, позволяет наиболее полно сохранить все преимущества модели и учитывает ее недостатки.
Похожие работы
... ) на передачу в ипотеку недвижимости или их непосредственное присутствие при заключении договора. РАЗДЕЛ 3. РАЗРАБОТКА МАРКЕТИНГОВОЙ СТРАТЕГИИ АКБ „ПРИВАТБАНК” В СЕГМЕНТЕ ИПОТЕЧНОГО КРЕДИТОВАНИЯ ЧАСТНЫХ ЛИЦ 3.1 Проблемы и возможности развития бизнеса АКБ „Приватбанк” в сегменте ипотечного кредитования частных лиц 3.1.1 Анализ проблем макросреды (PEST- анализ) В материалах формирования ...
... функция общей экономической теории – прогнозно-прагматическая, предполагающая разработку и выявление научных прогнозов и перспектив общественного развития. Эти функции экономической теории осуществляются в повседневной жизни цивилизованного общества. Экономической науке принадлежит огромная роль в формировании экономической среды в определении масштабов и направлений экономической динамики, в ...
... и ведомств, лицензии, уставные документы, нормы, инструкции, методические указания и др. Глава 2. Цели, задачи и сущность финансового менеджмента в условиях рыночной экономики. 2.1. Эволюция финансового менеджмента. В отличие от бухгалтерского учета, история которого насчитывает не одно тысячелетие, финансовый менеджмент как самостоятельная наука ...
... обслуживания и ремонта; - текущий мониторинг экономических показателей функционирования созданного предприятия. 2. Исследование и анализ структурно-инвестиционных процессов в экономике Республики Дагестан 2.1 Анализ динамики и структуры инвестиционной деятельности РД Республика Дагестан по уровню социально-экономического развития занимала в дореформенный период и занимает сейчас одно из ...




0 комментариев