Навигация
По известной процедуре МНК строим уравнения линейной парной регрессии для каждой из этих частей
4. По известной процедуре МНК строим уравнения линейной парной регрессии для каждой из этих частей.
Получаем для первой части: ![]() , для последней части:
, для последней части: ![]() .
.
Уже видим, что коэффициенты и а0, и а1 в этих уравнениях заметно отличаются. Это говорит о неоднородности вариации стат. данных, а, значит, о гетероскедастичности.
5. Находим остатки для каждого из этих уравнений, возводим их в квадрат и суммируем:
| Первая часть выборки |
| |||||||||||
| № | Потребление животного масла | Потребление растительное масло |
| ei | ei2 |
| ||||||
| Усть-Ордынский Бурятский авт. округ | 43,7 | 82,7 | 39,061 | -4,639 | 21,521 |
| ||||||
| Республика Тыва | 41 | 88 | 40,717 | -0,283 | 0,080 |
| ||||||
| Республика Калмыкия | 45,5 | 105,6 | 46,218 | 0,718 | 0,516 |
| ||||||
| Республика Ингушетия | 46,3 | 113 | 48,531 | 2,231 | 4,976 |
| ||||||
| Республика Адыгея | 50,8 | 138,4 | 56,469 | 5,669 | 32,139 |
| ||||||
| Республика Дагестан | 50,8 | 147,5 | 59,313 | 8,513 | 72,475 |
| ||||||
| Республика Марий Эл | 64,4 | 149,4 | 59,907 | -4,493 | 20,187 |
| ||||||
| Чувашская Республика | 55,9 | 149,7 | 60,001 | 4,101 | 16,817 |
| ||||||
| Республика Мордовия | 59,5 | 151,1 | 60,438 | 0,938 | 0,881 |
| ||||||
| Республика Алтай | 63,7 | 154,7 | 61,563 | -2,137 | 4,565 |
| ||||||
| Агинский Бурятский авт. округ | 73,2 | 162,8 | 64,095 | -9,105 | 82,900 |
| ||||||
| Кабардино-Балкарская Республика | 65,1 | 167 | 65,408 | 0,308 | 0,095 |
| ||||||
| Карачаево-Черкесская Республика | 66,9 | 167,2 | 65,470 | -1,430 | 2,044 |
| ||||||
| Забайкальский край | 79,9 | 167,3 | 65,501 | -14,399 | 207,319 |
| ||||||
| Кировская область | 53 | 168,3 | 65,814 | 12,814 | 164,198 |
| ||||||
| Республика Хакасия | 66,9 | 171,8 | 66,908 | 0,008 | 0,000 |
| ||||||
| Удмуртская Республика | 68,1 | 172,7 | 67,189 | -0,911 | 0,830 |
| ||||||
| Еврейская автономная область | 65,5 | 174 | 67,595 | 2,095 | 4,391 |
| ||||||
| Сумма | 1060,2 | 2631,2 | 1060,2 | 0,000 | 635,932 |
| ||||||
|
| ||||||||||||
| № | Употребление животного масла | потребление растительного масла |
| ei | ei2 | |||||||
| Краснодарский край | 83,1 | 252,1 | 92,935 | 9,835 | 96,725 | |||||||
| Республика Саха (Якутия) | 116,6 | 254,6 | 93,872 | -22,728 | 516,556 | |||||||
| Кемеровская область | 93,3 | 258,4 | 95,297 | 1,997 | 3,987 | |||||||
| Республика Башкортостан | 105,6 | 261,3 | 96,384 | -9,216 | 84,936 | |||||||
| Республика Татарстан | 118,5 | 266,8 | 98,446 | -20,054 | 402,168 | |||||||
| Омская область | 102,7 | 272,3 | 100,508 | -2,192 | 4,806 | |||||||
| Томская область | 107 | 273,5 | 100,958 | -6,042 | 36,510 | |||||||
| Красноярский край | 103,2 | 276,9 | 102,232 | -0,968 | 0,936 | |||||||
| Свердловская область | 104,2 | 285,1 | 105,306 | 1,106 | 1,224 | |||||||
| Чукотский авт. округ | 108,2 | 285,8 | 105,569 | -2,631 | 6,923 | |||||||
| Магаданская область | 99 | 290,6 | 107,368 | 8,368 | 70,031 | |||||||
| Камчатский край | 90,8 | 293,2 | 108,343 | 17,543 | 307,763 | |||||||
| Хабаровский край | 83,5 | 294 | 108,643 | 25,143 | 632,174 | |||||||
| Пермский край | 118,9 | 294,5 | 108,831 | -10,069 | 101,394 | |||||||
| Сахалинская область | 113,4 | 372,2 | 137,960 | 24,560 | 603,196 | |||||||
| Тюменская область | 173,3 | 455 | 169,002 | -4,298 | 18,477 | |||||||
| Ямало-Ненецкий авт. округ | 195,9 | 546,1 | 203,155 | 7,255 | 52,631 | |||||||
| Ханты-Мансийский авт. округ-Югра | 221,4 | 547,8 | 203,792 | -17,608 | 310,040 | |||||||
| Сумма | 2138,6 | 5780,2 | 2138,600 | 0,000 | 3250,477 | |||||||
6. Находим отношение большей суммы квадратов остатков к меньшей, оно подчиняется F-распределению Фишера. В данном случае ![]() , поэтому
, поэтому 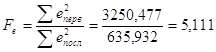 .
.
7. Сравниваем его с табличным значением F-критерия Фишера на уровне значимости d с (k-1) и (k-1) степенями свободы, где k – объёмы оставшихся частей выборки.
На уровне значимости d=0,05 с 17 и 17 степенями свободы табличное значение ![]() .
.
8. Выдвигаем гипотезу Н0 об отсутствии гетероскедастичности (выполнении предпосылки 2). Альтернативная ей Н1 о наличии гетероскедастичности (нарушении предпосылки 2).
9. Т.к. наблюдаемое значение превышает табличное: ![]() , то мы вынуждены принять гипотезу о наличии гетероскедастичности, подтвердив свои предположения о нарушении предпосылки 2.
, то мы вынуждены принять гипотезу о наличии гетероскедастичности, подтвердив свои предположения о нарушении предпосылки 2.
Возможно, этим объясняется большая ошибка аппроксимации.
Т.к. Fe не намного превышает Fтабл, то можно сказать, что последствия гетероскедастичности выражены несильно, и несильно сказываются на качестве модели. В данном случае эффективнее будет пренебречь этим несильным нарушением предпосылки 2, чем корректировать модель.
Предпосылка 3 О некоррелированности остатков
Т.к. выборка – пространственная, то для таких выборок нарушения этой предпосылки обычно несвойственно, т.к. не участвует фактор времени. Но чтобы убедиться в этом проверим Автокорреляцию остатков хотя бы 1-го уровня.
Полученные остатки сместим на 1 наблюдение – получим остатки 1-го уровня.
| № | ei | ei-1 | ei* ei-1 |
| Республика Адыгея | 4,5388 | ||
| Республика Дагестан | 7,742 | 4,5388 | 35,139 |
| Республика Ингушетия | 0,098 | 7,742 | 0,759 |
| Кабардино-Балкарская Республика | 0,306 | 0,098 | 0,030 |
| Республика Калмыкия | -1,7068 | 0,306 | -0,522 |
| Карачаево-Черкесская Республика | -1,4236 | -1,7068 | 2,430 |
| Республика Северная Осетия - Алания | 0,4644 | -1,4236 | -0,661 |
| Краснодарский край | 12,2612 | 0,4644 | 5,694 |
| Ставропольский край | 12,066 | 12,2612 | 147,944 |
| Астраханская область | -25,1124 | 12,066 | -303,006 |
| Волгоградская область | 0,6932 | -25,1124 | -17,408 |
| Ростовская область | 5,3412 | 0,6932 | 3,703 |
| Республика Башкортостан | -7,0004 | 5,3412 | -37,391 |
| Республика Марий Эл | -5,1892 | -7,0004 | 36,326 |
| Республика Мордовия | 0,3092 | -5,1892 | -1,605 |
| Республика Татарстан | -17,9644 | 0,3092 | -5,555 |
| Удмуртская Республика | -0,6876 | -17,9644 | 12,352 |
| Чувашская Республика | 3,4164 | -0,6876 | -2,349 |
| Пермский край | -8,614 | 3,4164 | -29,429 |
| Кировская область | 12,8636 | -8,614 | -110,807 |
| Нижегородская область | 6,3964 | 12,8636 | 82,281 |
| Оренбургская область | 6,0012 | 6,3964 | 38,386 |
| Пензенская область | -11,4804 | 6,0012 | -68,896 |
| Самарская область | 4,8812 | -11,4804 | -56,038 |
| Саратовская область | -16,8924 | 4,8812 | -82,455 |
| Ульяновская область | -4,4396 | -16,8924 | 74,995 |
| Курганская область | 6,31 | -4,4396 | -28,014 |
| Свердловская область | 2,7772 | 6,31 | 17,524 |
| Тюменская область | -6,518 | 2,7772 | -18,102 |
| Ханты-Мансийский авт. округ-Югра | -21,9524 | -6,518 | 143,086 |
| Ямало-Ненецкий авт. округ | 2,9492 | -21,9524 | -64,742 |
| № | ei | ei-1 | ei* ei-1 |
| Челябинская область | 0,8636 | 2,9492 | 2,547 |
| Республика Алтай | -2,6236 | 0,8636 | -2,266 |
| Республика Бурятия | -6,5572 | -2,6236 | 17,203 |
| Республика Тыва | -3,402 | -6,5572 | 22,308 |
| Республика Хакасия | 0,1956 | -3,402 | -0,665 |
| Алтайский край | 11,6428 | 0,1956 | 2,277 |
| Забайкальский край | -14,3884 | 11,6428 | -167,521 |
| Агинский Бурятский авт. округ | -9,2724 | -14,3884 | 133,415 |
| Красноярский край | 0,8908 | -9,2724 | -8,260 |
| Иркутская область | -8,8524 | 0,8908 | -7,886 |
| Усть-Ордынский Бурятский авт. округ | -7,9676 | -8,8524 | 70,532 |
| Кемеровская область | 4,2788 | -7,9676 | -34,092 |
| Новосибирская область | -2,9532 | 4,2788 | -12,636 |
| Омская область | -0,2284 | -2,9532 | 0,675 |
| Томская область | -4,106 | -0,2284 | 0,938 |
| Республика Саха (Якутия) | -20,3588 | -4,106 | 83,593 |
| Камчатский край | 19,0284 | -20,3588 | -387,395 |
| Приморский край | 6,0436 | 19,0284 | 115,000 |
| Хабаровский край | 26,61 | 6,0436 | 160,820 |
| Амурская область | 15,4124 | 26,61 | 410,124 |
| Магаданская область | 9,9132 | 15,4124 | 152,786 |
| Сахалинская область | 24,2364 | 9,9132 | 240,260 |
| Еврейская автономная область | 2,37 | 24,2364 | 57,440 |
| Чукотский авт. округ | -0,9764 | 2,37 | -2,314 |
| -0,9764 | |||
| Сумма от 2-го по 55-й | -4,3056 | 1,2099 | 620,554 |
| Ср. знач. | -0,080 | 0,022 | 11,4917331 |
| Станд. откл. | 10,36 | 10,486 |
Чтобы оценить отсутствие или наличие Автокорреляции 1-го уровня, выясним, есть ли зависимость между остатками модели и остатками 1-го уровня. Из-за смещения останется на 1 значение меньше – 22: со 2-го по 23-е наблюдение. Вычислим коэффициент корреляции между ei и ei-1 по его известной формуле:
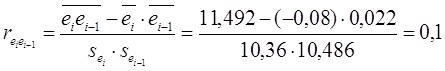
(где 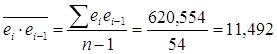 ).
).
Итак, коэффициент корреляции показывает, что зависимость слабая. Т.е. автокорреляция остатков 1-го уровня слабая. И т.к. выборка пространственная, то этим небольшим нарушением предпосылки 3 можно пренебречь.
Предпосылка 4 О некоррелированности значений фактора и остатков
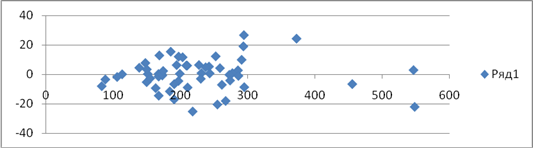
Построим поле корреляции между фактором Х и остатками е.
По этому расположению точек ![]() делаем вывод о том, ни закономерности, ни систематического смещения их не наблюдается.
делаем вывод о том, ни закономерности, ни систематического смещения их не наблюдается.
Рассчитываем коэффициент корреляции между фактором Х и остатками е (по обычной формуле): ![]() .
.
Значит, фактор Х и остатки е – некоррелированы. Предпосылка 4 не нарушена.
Предпосылки 1 и 5. О нормальном распределении остатков с нулевым матем. ожиданием
По значениям остатков модели построим интервальный вариационный ряд частот. Значения остатков изменяются от min(е)= --25,1124 до max(е)=24,2364. Тогда нижней границей будет -25, а верхней 24, длина всего этого интервала 25+24=49. Его удобно разбить на 7 интервалов. Пусть будет 7 интервалов, их длины 49/7=7. Считаем сколько значений еi попадает в каждый из них. И выписываем интервальный вариационный ряд в виде таблицы:
| Границы | [-25; -18) | [-18; -11) | [-11; -4) | [-4; 3) | [3; 10) | [10; 17) | [17; 24) |
| Частоты | 3 | 3 | 11 | 19 | 11 | 5 | 3 |
Строим по нему гистограмму частот.
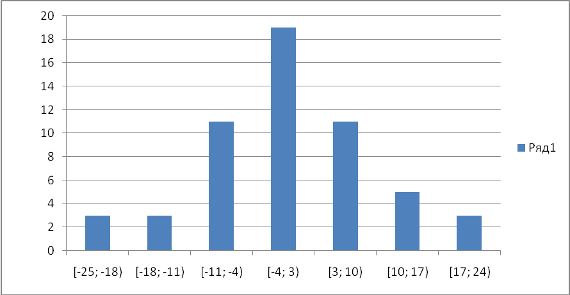
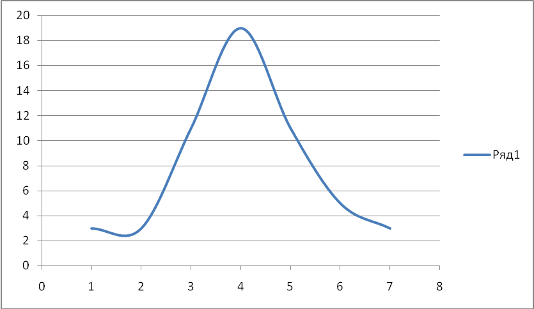
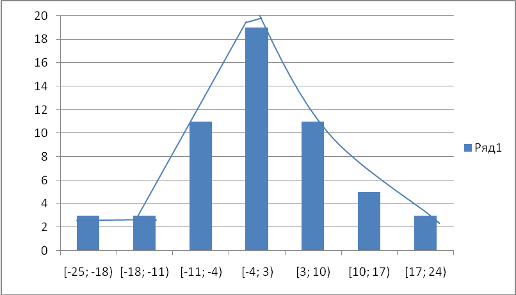
На этом же графике построим график кривой плотности нормального распределения (в соответствующем масштабе) с матем. ожиданием = 0 и сравним форму гистограммы и нормальной кривой.
Для данной выборки можно увидеть, что гистограмма частот остатков более-менее близка по форме к нормальной кривой. Но говорить уверенно о том, что остатки точно распределены нормально, нельзя. Возможно, при большем объёме выборки форма гистограммы была бы более понятной и однозначной.
В данном же исследовании на основании этого графика примем предположение о нормальности остатков. И будем считать, что предпосылки 1 и 5 не нарушены.
Выводы:
Высоко статистически значимые коэффициенты регрессии а0 и а1, коэффициент корреляции rух свидетельствуют о наличии сильной положительной взаимозаменяемости товаров. Это подтверждается и проверкой качества уравнения регрессии по F-критерию Фишера. Т.е., можно считать, что наличие взаимозаменяемости статистически доказано, направление и общая тенденция отражена уравнением регрессии верно и согласуется с состоянием рынка продовольственных товаров. Значения стандартных ошибок ![]() и
и ![]() для коэффициентов а0 и а1 малы, и доверительные интервалы для параметров модели a0 и a1 не широки, а также высокое значение коэффициента детерминации R2 указывают, что взаимозаменяемость потребления животного масла растительным маслом доказана. Влияние же других экономических (и случайных, в том числе) факторов – намного менее существенно.
для коэффициентов а0 и а1 малы, и доверительные интервалы для параметров модели a0 и a1 не широки, а также высокое значение коэффициента детерминации R2 указывают, что взаимозаменяемость потребления животного масла растительным маслом доказана. Влияние же других экономических (и случайных, в том числе) факторов – намного менее существенно.
Но средняя ошибка аппроксимации свидетельствует, что в среднем смоделированные данные отличаются от фактических на 9-12%. И в данном исследовании этот уровень можно признать условно приемлемым и только для изученного периода.
В данной модели обнаружена гетероскедастичность остатков. Она обусловлена рыночной ситуацией. Но она несильно нарушает предпосылку 2. Поэтому принято решение, не подвергать модель излишней корректировке, которая вряд ли улучшит её качество.
По результатам проверки остальных предпосылок МНК можно считать, что они выполнены, или, по крайней мере, их негативные последствия минимальны. Для более однозначного ответа требуется увеличение выборки.
Всё это означает, что применение полученного уравнения на другие периоды или другие регионы, и пр. для качественного и реального прогнозирования возможно только с определёнными поправками. И было бы целесообразным для повышения прогностической силы и практической ценности этой модели добавление в нее других факторов, изучение данных и за другие периоды.
Рекомендации по улучшению качества этой модели:
Увеличить выборку для повышения точности.
Добавить в модель и другие факторы (напр., цены на эти продукты, национальные предпочтения, удаленность от производства, сезонные особенности употребления этих продуктов и т. д.), чтобы улучшить аппроксимацию модели.
Внести корректировку для периода времени, чтобы модель была применима не только для изученного периода, ни и для других лет.
Из-за гетероскедастичности можно построить 5 модели: для каждого федерального округа.
Похожие работы
... , способствует непрерывности процесса воспроизводства. Так удельный вес розничного товарооборота республики в 2009г. занимал 40% в общем объеме ВВП страны. Следовательно, повышение конкурентоспособности торговых организаций будут способствовать обеспечению оптимального соотношения ее составляющих и элементов. При этом усилия направляются на повышение качества и снижение расходов на реализацию, ...
... эталоном, уровень качества равен 1; - карамель «Рачки с арахисом» и «Жалейка» обладает отличным качеством; - карамель «Каролинка» и «Коньячная» - имеет хорошее качество. 3. Коммерческая работа по организации хозяйственных связей с поставщиками кондитерских товаров на ЧУП «Гомельская универсальная база» Гомельского облпотребсоюза 3.1 Краткая организационно-экономическая характеристика ЧУП ...
... помещения магазина, торгово-технологическое оборудование, рабочую силу и в конечном итоге создать условия для обеспечения высокого качества обслуживания покупателей. В основу организации торгово-технологического процесса магазина должны быть положены товарные потоки. Под товарным потоком на розничном торговом предприятии понимается движение товаров от момента поступления до вручения проданного ...
... или огорода или которые вы приобретаете в магазине, являются сырьем для питания. Они очень разнообразны по своему характеру и качеству и для удобства классифицируются по составу и источнику происхождения. В естественном правильном питании очень большую важность имеет сочетание различных групп друг с другом. Для того чтобы правильно подбирать продукты для своего питания, необходимо знать, какие ...





0 комментариев