Дисперсионный анализ при помощи системы MINITAB для WINDOWS

Министерство образования и науки Украины

Севастопольский национальный технический

университет

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению лабораторной работы № 3 и 4

” Дисперсионный анализ при помощи системы

MINITAB для WINDOWS “

 

по учебной дисциплине “Прикладная статистика”

для студентов экономических специальностей

всех форм обучения

Севастополь

2008

Методические указания рассмотрены и утверждены на заседании кафедры менеджмента и экономико -математических методов протокол № “_____” от “______________” 2008г.

Рецензент: доцент департамента учета и аудита Т.А.Мараховская

1. Цель работы

Изучение возможностей дисперсионного анализа, для выявления зависимостей между экономическими показателями и получение практических навыков работы в системе MINITAB.

Теоретические сведения

 

2.1.     Дисперсионный анализ

 

2.1.1.  Однофакторный дисперсионный анализ

При проведении экономического анализа часто необходимо оценить влияние на целевую функцию y качественного фактора x _. Таким фактором могут быть, например, партии сырья, отрасли промышленности, регионы и т.д.

Пусть данные о влиянии некоторого качественного фактора на количественный в форме таблицы.

Таблица 1.1. – влияние качественного фактора на исследуемый показатель

		…
		….
		…
…	…	…	…

Модель зависимости значений от фактора столбцов можно представить в следующем виде [1-4]:

где - общее среднее, -отклонение от общего среднего для j-го уровня фактора, - случайная составляющая.

По выборочным данным можно вычислить:

1)         среднее  для каждого уровня фактора (среднее по столбцам)x_j (j=1,2,...u ), по m_j параллельным опытам, где m_j– число данных в столбце j:

;

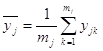2)         общее среднее  по всем N опытам, т.е. по всем m_j параллельным опытам на всех уровнях фактора x_j ():

;

3)         общую сумму квадратов отклонений Q₀:

4)         сумму квадратов, характеризующую влияние фактора x (отклонения между группами)

;

5)         остаточную сумму квадратов, зависящую от ошибки e (отклонения внутри групп)

.

Тождество дисперсионного анализа имеет вид:

На основании вычисленных сумм квадратов вычисляются:

1)         оценка дисперсии относительно общего среднего:

,

где  - число степеней свободы;

2) оценка дисперсии «между группами», определяемыми уровнями x_j:

где число степеней свободы .

3) выборочная оценка дисперсии «внутри групп», вычисляемая как средняя оценка по всем u группам:

с числом степеней свободы

Числа степеней свободы должны удовлетворять соотношению

Для того, чтобы сделать вывод о том, влияет ли на исследуемые показатели качественный фактор, сопоставляют дисперсию между группами с общей дисперсией. При этом выдвигают следующие гипотезы:

H₀:  , т.е средние значения по всем столбцам равны и равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам равно среднеквадратическому отклонению по всем данным и равно нулю. Т.е. качественный фактор не оказывает влияния на исследуемый показатель.

H₁: , , т.е средние значения по всем столбцам не равны между собой и не равны общему среднему, откуда следует, что среднеквадратическое отклонение по факторам не совпадает со среднеквадратическим отклонением по всем данным. Т.е. качественный фактор оказывает существенное влияние на исследуемый показатель.

Оценивание значимости влияния фактора x выполняется по F-критерию Фишера, для чего формируется следующее F-отношение:

.

Фактор x признается незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости  и числа степеней свободы сравниваемых дисперсий и _.

Табличное значение критерия Фишера определяется дл числа степеней свободы u-1 и N-1 и вероятности ошибки .

Т.е если , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.

Если , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.

Результаты дисперсионного анализа сводятся в таблицу 2.

  Таблица 2 Однофакторный дисперсионный анализ

Источник изменчивости	Сумма квадратов отклонений	Число степеней свободы	Оценка дисперсии	F – отношение
Между группами
Внутри групп ( ошибка e)
Общая сумма

 - число данных в столбце, u- число столбцов, m – число строк.