Навигация
Двухфакторный дисперсионный анализ при перекрестной
2.1.2. Двухфакторный дисперсионный анализ при перекрестной
классификации факторов
Часто необходимо качественно оценить значимость или незначимость влияния на целевую функцию u двух одновременно действующих факторов x1 и x2 . Такими факторами могут быть, например, форма собственности предприятия x1 ивид экономической деятельности x2.
Модель двухфакторного дисперсионного анализа имеет вид [1-4]:
![]()
где ![]() - общее среднее,
- общее среднее, ![]() -отклонение от общего среднего для фактора x1,
-отклонение от общего среднего для фактора x1, ![]() - отклонение от общего среднего для фактора x2,
- отклонение от общего среднего для фактора x2, ![]() - отклонение от общего среднего для взаимодействия двух факторов,
- отклонение от общего среднего для взаимодействия двух факторов, ![]() - случайная составляющая.
- случайная составляющая.
В этом случае общую сумму квадратов отклонений Q0 можно разбить на четыре суммы:
1) Qx1-по фактору x1,
2) Qx2-по фактору x2,
3) Qe-остаточную сумму квадратов, зависящую от ошибки e,
4) Q x1x2-зависящую от взаимодействия (произведения) x1x2 двух факторов.
В этом случае по выборочным значениям вычисляются:
1) среднее ![]() для каждого уровня фактораx1:
для каждого уровня фактораx1:
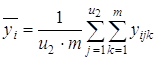 ;
;
2) среднее ![]() для каждого уровня фактора x2:
для каждого уровня фактора x2:
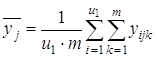 ;
;
3) общее среднее ![]() по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (
по всем N опытам, т.е. по всем m параллельным опытам на всех сочетаниях уровней факторов x1 и x2 (![]() ):
):
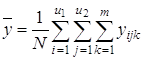 ;
;
4) среднее ![]() по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
по m параллельным опытам для каждого сочетания уровней факторов x1 и x2:
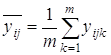 .
.
В табл.2 показаны данные полного факторного эксперимента с одинаковым числом наблюдений в ячейках.
Таблица 3. - Данные эксперимента и расчёты средних при двухфакторном дисперсионном анализе
| j = | 1 | 2 | … |
|
| |
|
| k |
|
| … |
| |
| 1 | 1 |
| ||||
| 2 |
| |||||
| … | … | |||||
| m |
| |||||
| . . . | 1 | |||||
| 2 | ||||||
| … | ||||||
| m | ||||||
|
| 1 | |||||
| 2 | ||||||
| … | ||||||
| m | ||||||
|
|
| |||||
В табл.2 ![]()
![]() вычисляется по выделенной части столбца, содержащей m параллельных опытов.
вычисляется по выделенной части столбца, содержащей m параллельных опытов.
Общая сумма квадратов отклонений Q0 рассчитывается по формуле:

Эту сумму можно разложить на 4 составляющие:
1) сумму, характеризующую влияние фактора x1:
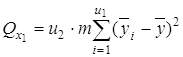 ;
;
2) сумму, характеризующую влияние фактора x2:
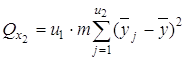 ;
;
3) сумму, характеризующую результат влияния взаимодействия x1x2:
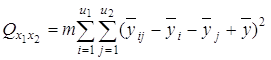
4) сумму, характеризующую влияние ошибки e:

Указанные пять сумм, поделенные на соответствующее число степеней свободы, дают пять различных оценок дисперсии, если влияние факторов x1 и x2 незначимо. Для проведения дисперсионного анализа вычисляются следующие дисперсии:
1) оценка дисперсии относительно общего среднего![]() :
:
![]() ,
,
где ![]() -общее число наблюдений, а число степеней свободы
-общее число наблюдений, а число степеней свободы
![]() ;
;
2) оценка дисперсии «между строками», определяемыми уровнями x1j:
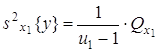 ,
,
где ![]() - число степеней свободы.
- число степеней свободы.
3) оценка дисперсии «между столбцами», соответствующими уровням фактора x2:
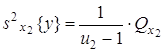 ,
,
где ![]() - число степеней свободы;
- число степеней свободы;
4) оценка дисперсии «между сериями» по m параллельным опытам каждая
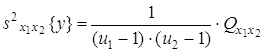
с числом степеней свободы ![]() ;
;
5) оценка дисперсии «внутри серий» по m параллельным опытам, вычисляемая как средняя оценка по всем u1u2 сериям:
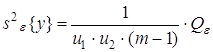
с числом степеней свободы ![]() .
.
Числа степеней свободы должны удовлетворять соотношению
![]()
Статистическое оценивание значимости влияния факторов x1 , x2 и взаимодействия x1x2 выполняются по F-критерию Фишера, для чего формируются следующие F-отношения:
 ,
, 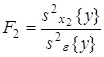 ,
, 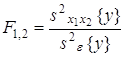 .
.
Фактор x1 или x2 , или взаимодействие x1x2 признаются незначимым, если соответствующее F-отношение оказывается меньше критического, выбранного из таблиц для принятого уровня значимости ![]() и числа степеней свободы сравниваемых дисперсий.
и числа степеней свободы сравниваемых дисперсий.
Для того, чтобы сделать вывод о том, влияют ли на исследуемые показатели качественные факторы, выдвигают следующие гипотезы:
H0: ![]() , т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем столбцам равны фактор столбца не оказывает влияния на исследуемый показатель.
H1: ![]() , , т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем столбцам не равны фактор столбца оказывает существенное влияние на исследуемый показатель.
H0: ![]() , т.е средние значения по всем строкам равны фактор строки не оказывает влияния на исследуемый показатель.
, т.е средние значения по всем строкам равны фактор строки не оказывает влияния на исследуемый показатель.
H1: ![]() , , т.е средние значения по всем строкам не равны фактор строки оказывает существенное влияние на исследуемый показатель.
, , т.е средние значения по всем строкам не равны фактор строки оказывает существенное влияние на исследуемый показатель.
H0: ![]() , т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо..
, т.е отклонение взаимодействия факторов равно нулю и взаимодействие не значимо..
H1: ![]() , фактор взаимодействия значим..
, фактор взаимодействия значим..
Если ![]() , то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
, то принимается нулевая гипотеза при соответствующем уровне значимости о том, что исследуемый фактор не оказывает существенного влияния на количественные данные.
Если ![]() , то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
, то нулевая гипотеза отвергается и принимается альтернативная при соответствующем уровне значимости. Исходя из этого, можно сделать вывод о том, что исследуемый фактор оказывает существенное влияние на количественные данные.
Результаты двухфакторного дисперсионного анализа представляются в виде табл.3.
Таблица 3. - Двухфакторный дисперсионный анализ при равном числе наблюдений в ячейках
| Вид изменчивости | Сумма квадратов отклонений | Число степеней свободы | Оценка дисперсии | F – отношение |
| От фактора x1 |
|
|
|
|
| От фактора x2 |
|
|
|
|
| От взаимо-действия x1x2 |
|
|
|
|
| Остаточная (от e) |
|
|
| |
| Общая |
|
|
|
m – число данных в строке (число повторов в ячейке), ![]() - число столбцов,
- число столбцов, ![]() - число строк.
- число строк.
Похожие работы
... MINITAB; - ознакомиться с информацией о Вашей версии MINITAB. После того как Вы завершить работу в статистическом пакете MINITAB необходимо для закрытия программы выполнить следующие команды: File > Exit. 2.4. Расчет основных статистик в пакете Minitab. В ходе выполнения лабораторной работы студент должен получить практические навыки и умения по следующим пунктам: - открывать и ...
... реакции или вмешательства оператора. Точки диалога по своей природе подразделяются на информационные (для ввода данных) и управляющие (для выбора дальнейшего хода обработки). Принятый в автоматизированной системе маркетинга одежды способ построения человеко-машинного диалога обеспечивает максимальную наглядность, простоту и удобство работы в режиме эксплуатации. 3. Определение емкости, оценка ...

 i =
i =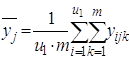
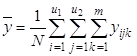
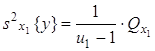
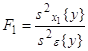
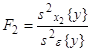
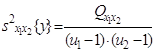
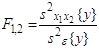
0 комментариев