Навигация
2.1 Виды распределений
2.1.1 Равномерное распределение
Функция плотности вероятности равномерного распределения задает одинаковую вероятность для всех значений, лежащих между минимальным и максимальным значениями переменной. Другими словами, вероятность того, что значение попадает в указанный интервал. пропорциональна длине этого интервала. Применение равномерного распределения часто вызвано полным отсутствием информации о случайной величине, кроме ее предельных значений. Равномерное распределение называют также прямоугольным.
f (t) =![]() при а ≤ t ≤ Ь.
при а ≤ t ≤ Ь.
Среднее значение распределения равно μ = ![]() , дисперсия равна σ2=
, дисперсия равна σ2=![]() .
.
Равномерно распределенная случайная величина X на отрезке [а, b] выражается через равномерно распределенную на отрезке [0, 1] случайную величину R формулой
X = а + (b - а) *R
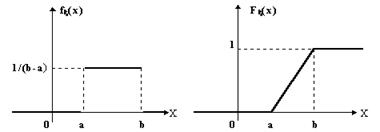
Рис.1 Графики функции распределения и плотности распределения:
2.1.2 Треугольное распределение
Треугольное распределение является более информативным, чем равномерное. Для этого распределения определяются три величины - минимум, максимум и мода. График функции плотности состоит из двух отрезков прямых, одна из которых возрастает при изменении X от минимального значения до моды, а другая убывает при изменении X от значения моды до максимума. Значение математического ожидания треугольного распределения равно одной трети суммы минимума, моды и максимума. Треугольное распределение используется тогда, когда известно наиболее вероятное значение на некотором интервале и предполагается кусочно-линейный характер функции плотности. Функция плотности вероятности треугольного распределения имеет вид:
|
|
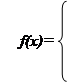
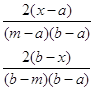
μ=![]() , σ2=
, σ2=![]() .
.
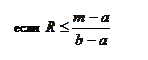
Треугольно распределенная случайная X связана со случайной величиной R, распределенной равномерно на [0,1], соотношением:
|
|
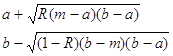
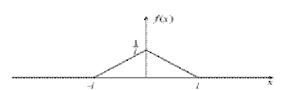
Рис.2 График плотности треугольного распределения
2.1.3 Экспоненциальное (показательное) распределение
Если вероятность того, что один и только один результат наступит на интервале Δt, пропорциональна Δt и если наступление результата не зависит от наступления других результатов, величины интервалов между результатами распределены экспоненциально. Другими словами, работа, продолжительность которой экспоненциально распределена имеет одинаковую вероятность завершения в течение любого последующего периода времени Δt. Таким образом, работа, выполняемая за t единиц времени, имеет ту же вероятность окончания в последующий период Δt, что и только что начатая работа. Подобное отсутствие временной обусловленности называется марковским свойством или свойством отсутствия последействия. Существует прямая связь между предположением об экспоненциальности распределения продолжительности работы и марковским свойством. Экспоненциальное распределение предполагает значительную вариабельность переменной. Если математическое ожидание продолжительности работы равно 1/α, то дисперсия равна 1/α2. По сравнению с большинством остальных распределений экспоненциальное обладает большей дисперсией.
Функция распределения:
![]()
|
Похожие работы
... на лазерные компакт-диски. Система моделирования Орлан ориентирована на достаточно широкий круг пользователей. В первую очередь, естественно, это администраторы вычислительных сетей предприятий, стоящие перед задачей проектирования или исследования сети. Обязательное условие, накладываемое системой – проектируемая сеть должны основываться на стандарте Ethernet. Но, так как абсолютное ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
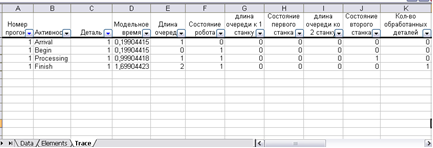
... характером квазипараллельного процесса является коренной причиной их неполного соответствия. Рисунок 1.2 — Динамика взаимодействия элементов СС. 2 СРЕДСТВА РЕАЛИЗАЦИИ ИМИТАЦИОННОЙ МОДЕЛИ 2.1 Табличный процессор Excel Имитационная модель автоматизированного участка обработки деталей реализована при помощи табличного процессора MS Excel и встроенной среды программирования Visual Basic for ...
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...



0 комментариев