Навигация
α >0 - параметр экспоненциального закона.
С экспоненциальным распределением легко осуществлять математические преобразования, благодаря чему оно применяется в целом ряде исследований.
Методом обратных функций можно показать, что показательно распределенная случайная величина X связана со случайной величиной R, распределенной равномерно на [0,1], соотношением:
Y=-1/α * ln(1-R),
где α - параметр показательного закона.
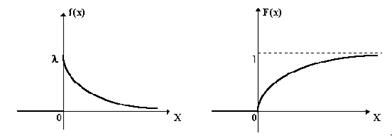
Рис.3 Графики функции распределения и плотности распределения
2.1.4 Распределение Пуассона
Распределение Пуассона является дискретным и обычно связано с числом результатов за определенный период времени. Если продолжительность интервалов между результатами распределена экспоненциально, и в каждый момент времени может произойти только один результат, то можно доказать, что число результатов на фиксированном интервале времени распределено по закону Пуассона. Другими словами, если интервалы между прибытиями распределены экспоненциально, распределение числа прибытий будет пуассоновским.
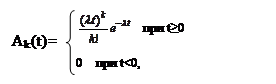
где λ>0, k≥0 - параметры закона. Пуассоновское распределение используется часто как аппроксимация биномиального распределения в том случае, когда оно моделирует последовательности независимых испытаний Бернулли (результаты таких испытаний могут быть типа «да-нет», «стоять-идти», «успех-неудача» и т.п.). При больших значениях математического ожидания пуассоновское распределение аппроксимируется нормальным.
Для получения пуассоновски распределенной случайной величины Y можно воспользоваться следующим методом: установить значение величины Y равным первому значению N, такому, что
|
где Rn – п-е псевдослучайное число.
2.1.5 Нормальное распределение
Нормальное, или Гауссово, распределение является наиболее важным в теории вероятностей и математической статистике. Эту роль нормальное распределение приобрело в связи с центральной предельной теоремой, которая утверждает, что при весьма нестрогих условиях распределение средней величины или суммы N независимых наблюдений из любого распределения стремиться к нормальному по мере увеличения N. Таким образом, сумму случайных величин часто можно считать нормально распределенной.
Именно благодаря центральной предельной теореме нормальное распределение так часто применяется в исследованиях по теории вероятностей и математической статистике. Существует и другая причина частого применения нормального распределения. Его преимуществом является легкость математического трактования, в связи с чем многие методы доказательств в таких областях, как, например, регрессионный или вариационный анализ, основаны на предположении о нормальном характере функции плотности.
При больших значениях среднего нормальное распределение является хорошей аппроксимацией биноминального распределения.
Функция плотности вероятности нормального закона имеет вид:
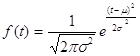
![]() - параметры нормального закона, (
- параметры нормального закона, (![]() - среднее значение,
- среднее значение, ![]() - дисперсия нормального распределения).
- дисперсия нормального распределения).
Генератор нормально распределенной случайной величины X можно получить по формулам:
![]()
где Tj (j=1,…,12) – значения независимых случайных величин, равномерно распределенных на интервале (0,1).
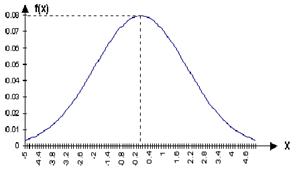
Рис. 4 График плотности вероятности имеет вид нормальной кривой (Гаусса)
2.2 Виды генераторов случайных чисел
Следует помнить, что генерация произвольного случайного числа состоит из двух этапов:
· генерация нормализованного случайного числа (то есть равномерно распределенного от 0 до 1);
· преобразование нормализованных случайных чисел ri в случайные числа xi, которые распределены по необходимому пользователю (произвольному) закону распределения или в необходимом интервале.
Генераторы случайных чисел (ГСЧ) по способу получения чисел делятся на:
µ физические;
µ табличные;
µ алгоритмические.
Похожие работы
... на лазерные компакт-диски. Система моделирования Орлан ориентирована на достаточно широкий круг пользователей. В первую очередь, естественно, это администраторы вычислительных сетей предприятий, стоящие перед задачей проектирования или исследования сети. Обязательное условие, накладываемое системой – проектируемая сеть должны основываться на стандарте Ethernet. Но, так как абсолютное ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
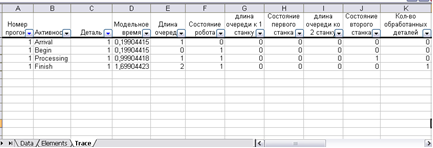
... характером квазипараллельного процесса является коренной причиной их неполного соответствия. Рисунок 1.2 — Динамика взаимодействия элементов СС. 2 СРЕДСТВА РЕАЛИЗАЦИИ ИМИТАЦИОННОЙ МОДЕЛИ 2.1 Табличный процессор Excel Имитационная модель автоматизированного участка обработки деталей реализована при помощи табличного процессора MS Excel и встроенной среды программирования Visual Basic for ...
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...



0 комментариев