Навигация
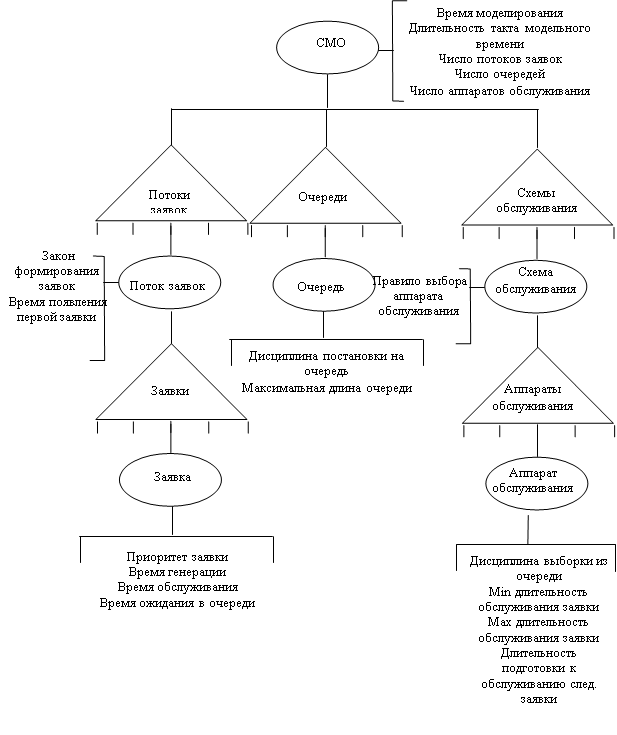
3.2. Описание метода решения
3.2.1 Описание метода решения задачи вручную
Трудность решения задачи ручным методом состоит в огромном количестве расчетов, которые необходимо произвести. Учитывая это, мы моделируем работу СТО не в течение 5 дней, как указано это в условии задания, а берем небольшой промежуток времени.
В курсовой работе при разработке модели работы СТО применены следующие виды распределения: равномерное и экспоненциальное.
Определим время прибытия автомобилей на СТО, которое имеет экспоненциальное распределение, и рассчитывается по следующей формуле:
u = - ln (g i) * λ , λ=1/14 маш./мин (1)
где gi – это случайные числа.
С помощью алгоритмической генерации случайных чисел, используя метод средних квадратов, сгенерировали 30 случайных чисел, которые представлены в таблице 2.
Подставляя полученные случайные числа в формулу (1) получим интервалы времени между поступлениями общего потока автомобилей на СТО, и занесем данные в таблицу 3.
Таблица 3.
| № | Случайные числа, g i | Время поступления требований, | Блоки, на которые поступают машины |
| 1 | 0,0850 | 34,51 | Тех.обслуживание |
| 2 | 0,2369 | 20,16 | Тех.обслуживание |
| 3 | 0,3412 | 15,05 | Тех.обслуживание |
| 4 | 0,9304 | 1,01 | Слож. ремонт |
| 5 | 0,9716 | 0,40 | Слож. ремонт |
| 6 | 0,1184 | 29,87 | Тех.обслуживание |
| 7 | 0,2838 | 17,63 | Тех.обслуживание |
| 8 | 0,2065 | 22,08 | Тех.обслуживание |
| 9 | 0,0139 | 59,86 | Тех.обслуживание + сред. ремонт |
| 10 | 0,6523 | 5,98 | Средний ремонт |
| 11 | 0,4056 | 12,63 | Простой ремонт |
| 12 | 0,6892 | 5,21 | Средний ремонт |
| 13 | 0,8028 | 3,08 | Слож. ремонт |
| 14 | 0,1368 | 27,85 | Тех.обслуживание |
| 15 | 0,3270 | 15,65 | Тех.обслуживание |
| 16 | 0,6431 | 6,18 | Средний ремонт |
| 17 | 0,6446 | 6,15 | Средний ремонт |
| 18 | 0,8252 | 2,69 | Слож. ремонт |
| 19 | 0,2025 | 22,36 | Тех.обслуживание |
| 20 | 0,6429 | 6,18 | Средний ремонт |
| 21 | 0,9519 | 0,69 | Слож. ремонт |
| 22 | 0,1202 | 29,66 | Тех.обслуживание |
| 23 | 0,9800 | 0,28 | Слож. ремонт |
| 24 | 0,1061 | 31,41 | Тех.обслуживание |
| 25 | 0,1841 | 23,69 | Тех.обслуживание |
| 26 | 0,6490 | 6,05 | Средний ремонт |
| 27 | 0,0809 | 35,20 | Тех.обслуживание |
| 28 | 0,2589 | 18,92 | Тех.обслуживание |
| 29 | 0,9340 | 0,96 | Слож. ремонт |
| 30 | 0,4139 | 12,35 | Простой ремонт |
Согласно условию задачи 36% автомобилей поступают на техническое обслуживание, а остальные 64% - на ремонт. Сравниваем доли процентов со случайными числами и, таким образом, определяем, какой именно автомобиль куда поступает:
· если g < 0.36, то на тех. обслуживание;
· если g > 0.36, то на ремонт.
Итого, из потока, поступающих на заправочную станцию 30 автомобилей, 15 автомобилей поступают на тех. обслуживание и 15 - на ремонт.
Далее, умножаем случайные числа, которые меньше 0,36 на 2,78. Это мы делаем для того, чтобы получить 100% из тех 36% машин, которые приехали на тех. обслуживание. Это поможет найти те самые 12% машин, которые после тех. обслуживания поступают на выполнение ремонта средней сложности. Полученные числа сравниваем – если число меньше или равно 0,12, то она после тех.обслуживания поступает и на средний ремонт. После произведенных вычислений мы определили, что 7ая машина, поступившая на тех. обслуживание, поступила также и на ремонт средней сложности.
Далее используем тот же метод для определения того, какие машины, поступившие на ремонт, поступили на простой, средний и сложный ремонты. Умножаем случайные числа, которые больше 0,36 на 1,56. Получившиеся числа сравниваем:
· если число < 0,33 – простой ремонт;
· если число находится в промежутке от 0,33 до 0,66 – средний ремонт;
· если число > 0,66 – сложный ремонт.
Далее определяем время на обслуживание автомобилей.
Ë Время на тех. обслуживание равномерно распределено в интервале 10-55:
Xтоi = gi (55 - 10) + 10
Стоимость тех.обслуживания также равномерно распределена в интервале 100-400:
Xтоi = gi (400 - 100) + 100
Таблица 4.
| № | Случайные числа, g i | Время обслуживания, мин | Случайные числа, g i | Стоимость обслуживания, руб |
| 1 | 0,3051 | 23,7295 | 0,663788 | 299,1364 |
| 2 | 0,4534 | 30,403 | 0,131907 | 139,5721 |
| 3 | 0,6705 | 40,1725 | 0,413686 | 224,1058 |
| 4 | 0,8613 | 48,7585 | 0,807198 | 342,1594 |
| 5 | 0,8378 | 47,701 | 0,950983 | 385,2949 |
| 6 | 0,1666 | 17,497 | 0,527365 | 258,2095 |
| 7 | 0,1816 | 18,172 | 0,735827 | 320,7481 |
| 8 | 0,0582 | 12,619 | 0,05409 | 116,227 |
| 9 | 0,0319 | 11,4355 | 0,022308 | 106,6924 |
| 10 | 0,382 | 27,19 | 0,105635 | 131,6905 |
| 11 | 0,5775 | 35,9875 | 0,817392 | 345,2176 |
| 12 | 0,5199 | 33,3955 | 0,599275 | 279,7825 |
| 13 | 0,8518 | 48,331 | 0,281503 | 184,4509 |
| 14 | 0,999 | 54,955 | 0,703246 | 310,9738 |
| 15 | 0,6651 | 39,9295 | 0,158009 | 147,4027 |
Для определения общей стоимости тех. обслуживания сложим все отдельные стоимости:
299,14 + 139,57 + 224,1 + 342,16 + 385,29 + 258,2 + 320,75 + 116,23 + 106,69 + 131,69 + 345,22 + 279,78 + 184,45 + 310,97 + 147,4 = 3591,664
Ë Время на простой ремонт равномерно распределено в интервале 12-45:
Xпрi = gi (45 - 12) + 12
Стоимость простого ремонта также равномерно распределена в интервале 50-450:
Xпрi = gi (450 - 50) + 50
Таблица 5.
| № | Случайные числа, g i | Время ремонта, мин. | Случайные числа, g i | Стоимость ремонта, руб. |
| 1 | 0,65671 | 33,67143 | 0,576774 | 280,7096 |
| 2 | 0,529158 | 29,46221 | 0,423461 | 219,3844 |
| 500,094 | |||
Ë Время на средний ремонт имеет экспоненциальное распределение со средним 45 и среднеквадратическим отклонением 5:
Xслi = ![]()
Стоимость среднего ремонта также равномерно распределена в интервале 100-1400:
Xслi = gi (1400 - 100) + 100
Таблица 6.
| № | Случайные числа, g 1i | Случайные числа, g 2i | Время ремонта, мин. | Случайные числа, g i | Стоимость ремонта, руб. |
| 1 | 0,65671 | 0,970213 | 43,34725 | 0,481822 | 726,3686 |
| 2 | 0,529158 | 0,620039 | 48,74525 | 0,034647 | 145,0411 |
| 3 | 0,460358 | 0,349485 | 49,32399 | 0,75438 | 1080,694 |
| 4 | 0,445785 | 0,761956 | 41,91791 | 0,194049 | 352,2637 |
| 5 | 0,840672 | 0,978321 | 44,21576 | 0,852098 | 1207,727 |
| 6 | 0,423906 | 0,688784 | 46,04819 | 0,778864 | 1112,523 |
| 7 | 0,763808 | 0,273752 | 46,6651 | 0,653691 | 949,7983 |
| 5574,416 | ||||
Ë Время на сложный ремонт равномерно распределено в интервале 80-150:
Xпрi = gi (150 - 80) + 80
Стоимость сложного ремонта также равномерно распределена в интервале 350-2550:
Xпрi = gi (2550 - 350) + 350
Таблица 7.
| № | Случайные числа, g i | Время ремонта, мин. | Случайные числа, g i | Стоимость ремонта, руб. |
| 1 | 0,471298 | 112,9909 | 0,831532 | 2179,37 |
| 2 | 0,548324 | 118,3827 | 0,631296 | 1738,851 |
| 3 | 0,752037 | 132,6426 | 0,82604 | 2167,288 |
| 4 | 0,270129 | 98,90903 | 0,910576 | 2353,267 |
| 5 | 0,37024 | 105,9168 | 0,231733 | 859,8126 |
| 6 | 0,914679 | 144,0275 | 0,351011 | 1122,224 |
| 7 | 0,058792 | 84,11544 | 0,274889 | 954,7558 |
| 11375,57 | |||
Нужно определить среднее время обслуживания автомобилей на СТО. Для этого сначала определяем среднее время обслуживания для ТО, простого, среднего и сложного ремонтов в отдельности.
Ø Среднее время тех. обслуживания = общее время тех. обслуживания / число обслуживающихся машин. = 480 / 15 = 32 мин.
Ø Среднее время простого ремонта = общее время простого ремонта / число обслуживающихся машин. = (50+43) / 2 = 46,5 мин.
Ø Среднее время среднего ремонта = общее время среднего ремонта / число обслуживающихся машин. = 466 / 7 = 66,57 мин.
Ø Среднее время сложного ремонта = общее время сложного ремонта / число обслуживающихся машин. = (64+27+27+66+37) / 7 = 31,57 мин.
Ø Общая стоимость обслуживания на СТО = 3591,664 + 500,094 + 5574,416 + 11375,57 =
21041,74 руб.
Итого среднее время обслуживания автомобилей = (32+46,5+66,57+31,57) / 4 = 44,16 мин.
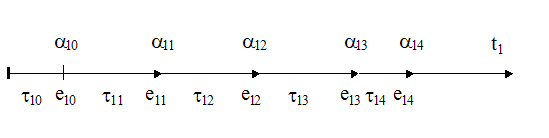
Для более детального моделирования работы заправочной станции, изобразим нашу СМО в виде графика (график прилагается к работе в виде Приложения).
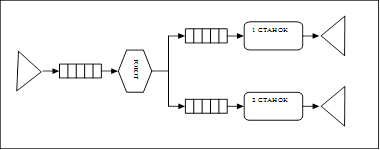
Интервал времени обслуживания всех машин на графике составляет 546 мин. Имеется 5 обслуживающих блоков: 2 блока для ТО, и по 1 блоку на простой, средний и сложный ремонты.
В каналы поступает один тип заявок – неприоритетные, т.е. поступающие заявки упорядочиваются в очереди и поступают на обслуживание в порядке поступления (первый пришел – первый обслужен).
Канал может обслуживать одновременно только одну заявку. Обслуживание заявок производится в таком порядке: сначала в очереди нет ни одной машины, и колонка свободна. В момент поступления машины начинается его обслуживание. Если следующая машина приезжает в тот момент, когда канал занят, то она становится в очередь. Далее дисциплина обслуживания такова: обслуживается машина, стоящая первая в очереди.
(См. Приложение).
По полученному графику определяем следующие характеристики работы СМО:
« Среднее время задержки (автомобилей): ![]()
Тех. обслуживание: (11+38+26) /3 = 25
Простой ремонт: нет задержки
Средний ремонт: 265 / 6 = 44,2
Сложный ремонт: 42 / 2 =21
« Средняя длина очереди (автомобилей): 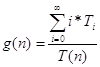 ,
,
Где: T(n) – конечное время работы системы;
T0, T1, T2 … - промежуток времени, в течении которого в системе находилось соответственно 0, 1, 2 и более требований.
Тех. обслуживание: T(n)=546; T0=471; T1=75; g(n) = 75 / 546 = 0,14
Простой ремонт: нет очереди
Средний ремонт: T(n)=515; T0=249; T1=128, T2=108, T3=29; g(n) = (128+108*2+29*3) / 515 = 0,84
Сложный ремонт: T(n)=493; T0=451; T1=42; g(n) = 42 / 491 = 0,09
« Максимальная длина очереди (автомобилей): L(max) = 3 машины
« Коэффициент использования устройства (блоков на СТО):
![]() ;
; ![]() ;
;
Тех. обслуживание: Un = 480 / 546 = 0,88 => 88% - работает, 12% - простой;
Простой ремонт: Un = 92/ 517 = 0,18 => 18% - работает, 72% - простой;
Средний ремонт: Un = 316 / 546 = 0,61 => 61% - работает, 39% - простой;
Сложный ремонт: Un = 221 / 546 = 0,45 => 45% - работает, 55% - простой.
3.3 Блок – схема
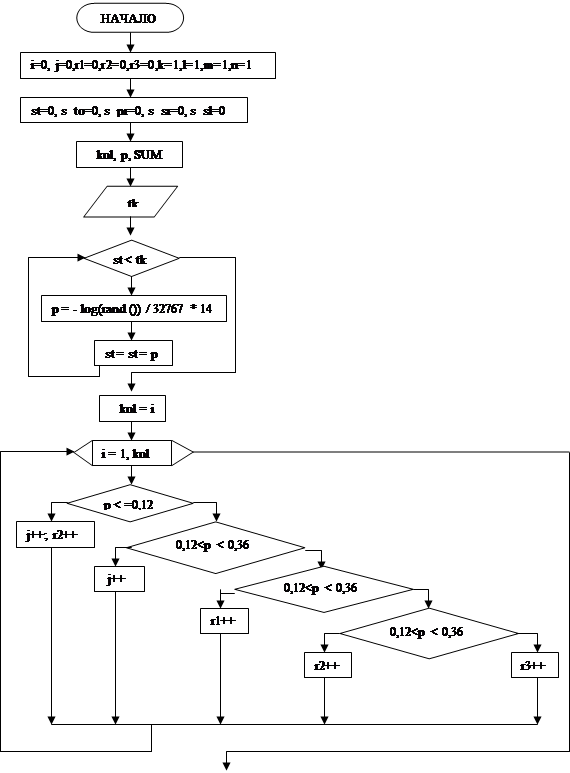 |
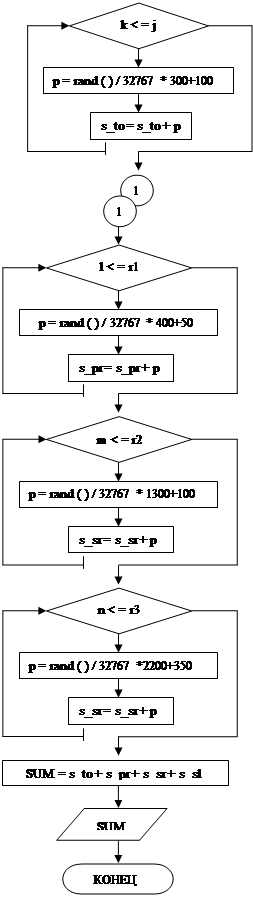 |
Похожие работы
... на лазерные компакт-диски. Система моделирования Орлан ориентирована на достаточно широкий круг пользователей. В первую очередь, естественно, это администраторы вычислительных сетей предприятий, стоящие перед задачей проектирования или исследования сети. Обязательное условие, накладываемое системой – проектируемая сеть должны основываться на стандарте Ethernet. Но, так как абсолютное ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...
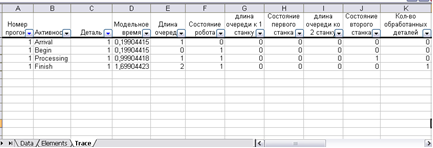
... характером квазипараллельного процесса является коренной причиной их неполного соответствия. Рисунок 1.2 — Динамика взаимодействия элементов СС. 2 СРЕДСТВА РЕАЛИЗАЦИИ ИМИТАЦИОННОЙ МОДЕЛИ 2.1 Табличный процессор Excel Имитационная модель автоматизированного участка обработки деталей реализована при помощи табличного процессора MS Excel и встроенной среды программирования Visual Basic for ...
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...



0 комментариев