Нахождение максимального потока

4.    Нахождение максимального потока.

Найти максимальный поток можно одним из нижеописанных способов.

4.1 Серия последовательных шагов.

На графиках укажем степень насыщения потока над каждым ребром, а в скобках остаточную пропускную способность.

Шаг 1: построим поток 1-2-3-4-5-6-7 и найдем максимальную пропускную способность этого пути.

 

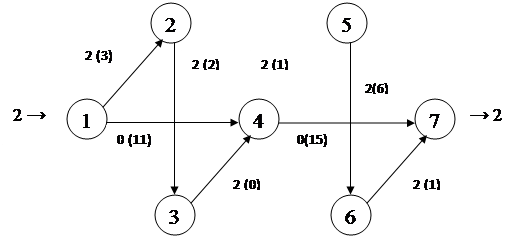Min (C_ij) = C₃₄ = 2

Φ₁ = 2

 

 

 

 

 

 

 

Поток не полный

 

Шаг 2: построим поток 1-4-5-6-7

Min (C_ij) = C₄₅ = 1

Φ₂ = Φ₁ + 1= 3

 

 

 

 

 

 

 

 

Поток не полный

 

 

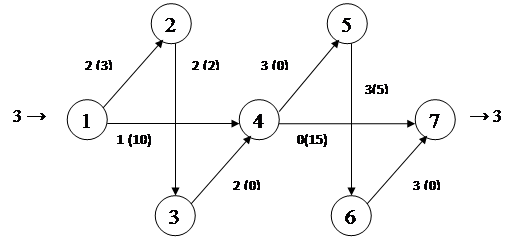
Шаг 3: построим поток 1-4-7

Min (C_ij) = C₁₄ = 10

Φ₃ = Φ₂ + 10= 13

 

 

 

 

 

 

 

 

Φ₃ =13 – полный поток

 

4.2           Метод разделяющих сечений

Обозначим все возможные разделяющие сечения данной сети и опишем их характеристики ниже.

 

 

 

 

 

 

 

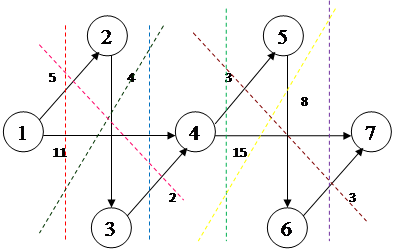1)                 Χ = {1},  = {2, 3, 4, 5, 6, 7}

С₁ = С(1; 2) + С(1; 3) = 5+11=16

2)                 Χ = {1, 2},  = {3, 4, 5, 6, 7}

С₂ = С(1; 4) + С(2; 3) = 11+4=15

3)                 Χ = {1, 3},  = {2, 4, 5, 6, 7}

С₃ = С(1; 2) + С(2; 3) + С(1, 4) + С(3, 4) = 5+4+11+2=22

4)                 Χ = {1, 2, 3},  = {4, 5, 6, 7}

С₄ = С(1; 4) + С(3, 2) = 11+2=13

5)                 Χ = {1, 2, 3, 4},  = {5, 6, 7}

С₅ = С(4; 5) + С(4, 7) = 3+15=18

6)                 Χ = {1, 2, 3, 4, 5},  = {6, 7}

С₆ = С(4; 7) + С(5, 6) = 8+15=23

7)                 Χ = {1, 2, 3, 4, 6},  = {5, 7}

С₇ = С(4; 5) + С(4, 7) + С(5, 6) + С(6, 7) = 3+15+8+3=29

8)                 Χ = {1, 2, 3, 4, 5, 6},  = {7}

С₈ = С(4; 7) + С(6, 7) = 15+3=18

Минимальное сечение:

Max Φ = min C_i = min(16, 15, 22, 13, 18, 23, 29, 18) = 13

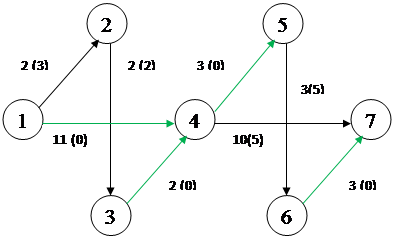
4.3           Ребра, обеспечивающие пропуск максимального потока через заданную сеть – выделены зеленым цветом. В скобках указана неиспользованная пропускная способность ребра.

4.4            

 

 

 

Пример:

Компания, занимающаяся прокладкой газопровода, решает задачу о замене некоторых участков, в связи с увеличившимся спросом у потребителей. Для этого необходимо выявить «узкие» участки газопровода. Пропускные способности каждого участка указаны рядом с ребрами.

После построения полного и максимального потока видно, что участки 1 – 4, 3 – 4, 4 – 5, 6 – 7 нагружены полностью, в то время как на участках 1 – 2, 2 – 3, 4 – 7, 5 – 6 не использована пропускная способность в размерах 3, 2, 5, 5 соответственно.

Раздел II. «Использование метода анализа иерархий для организации поставок»

Предприятие решает вопрос о продлении договора на поставку с одним из поставщиков, основываясь на результатах работы по уже заключенным договорам. Поставщики оцениваются по критериям:

К1 – надежность поставки

К2 – цена

К3 – качество товара

К4 – условия платежа

К5 – возможность внеплановых поставок

Матрица сравнений критериев относительно цели:

 

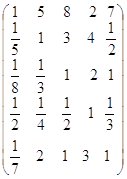Матрицы сравнения альтернатив (поставщиков) относительно критериев:

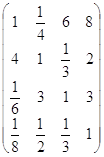k1 k2 k3 k4 k5

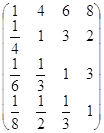
Найдем веса критериев и проверим согласованность матрицы сравнения критериев. При несогласованности матрицы найдем противоречия в суждениях ЛПР, изменим результаты сравнения и проверим согласованность матрицы заново.

Для матрицы сравнения критериев относительно цели найдем собственный вектор и вес каждого критерия:

Критерий	k1	k2	k3	k4	k5	собственный вектор	вес
k1	1	5	8	2	7	3,545	0,535
k2	1/5	1	3	4	1/2	1,037	0,157
k3	1/8	1/3	1	2	1	0,608	0,092
k4	1/2	1/4	1/2	1	1/3	0,461	0,070
k5	1/7	2	1	3	1	0,970	0,146
					Σ	6,621	1,000

Проверим согласованность матрицы:

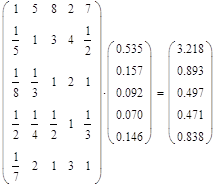
n = 5

L = 0,229

R = 1,120

T = 0,204 > 0,1 – уровень согласованности не приемлем.

Изменим суждения ЛПР для достижения согласованности матрицы.

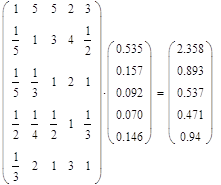
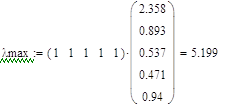
n = 5

L = 0,049

R = 1,120

T = 0,043 < 0,1 – уровень согласованности приемлем.