Навигация
Оцінимо параметри регресії за допомогою 1МНК
1. Оцінимо параметри регресії за допомогою 1МНК.
Підготуємо необхідні проміжні матриці:
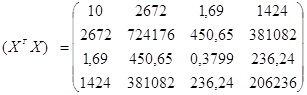
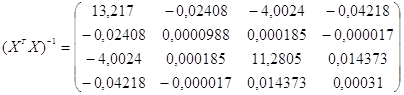
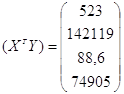
Використовуючи оператор оцінювання МНК, отримуємо
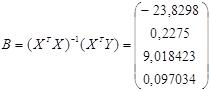
Þ Рівняння регресії має вигляд:
Y = -23,83+0,23X1+9,018X2+0,097X3
Ця модель має бути проаналізована на значущість в цілому (2), а також на значущість кожного коефіцієнта регресії зокрема (3).2. Перевірка значущості моделі
Значущість всієї моделі в цілому будемо проводити для рівня значущості a=0,05 за допомогою F-крітерія при (m-1) і (n-m) ступенях свободи. Розрахункове значення F-критерію розраховується по формулі:
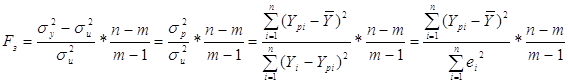
де ![]() ,
, ![]()
Y – спостеріганні значення фактора (вихідні дані),
n – число спостережень,
m – число оцінюваних параметрів.
Нульова гіпотеза для перевірки значущості моделі: Н0: b0 = b1 = …… = bm= 0.
Проведемо необхідні попередні розрахунки.
Використовуючи вихідну матрицю Х і побудовану модель, отримуємо розрахункові Yp:
Yp = X*BT і залишки е = Y - Yp :


Сума квадратів відхилень значень регресії від середнього та сума залишків дорівнює:
![]() 583,5752
583,5752 ![]() ,
,
![]()
Табличне значення для (m-1), (n-m) F-критерію (0,95) = 4,76. Оскільки Fp>Fтабл , модель можна вважати статистично значимою. (нульова гіпотеза відхиляється).
Далі оцінюєтья значущість кожного з параметрів bj.за допомогою t-статистики.
3. Оцінка значущості окремих коефіцієнтів регресії.
Гіпотезу про значущість кожного з параметрів bj економетрічної моделі можна виконати за допомогою t-крітерію. Нульова гіпотеза, найбільш поширена притестуванні економетричної моделі - bjнесуттєво відрізняються від 0, тобто H0: bj = 0. Поширеність такої постанови нульової гіпотези – в тому, що якщо вона підтверджується, то це має означати, що відповідний Xj статистично незначущо впливає на Y, його вплив з високою вірогідністю дорівнює 0, залежності між Y та Х практично немає і відповідна змінна повинна бути виключена з моделі. Виключенням є випадок, коли при незначущому bj залежність між X і Y таки існує, але нелінійна. В цьому випадку треба змінити специфікацію моделі (надати їй іншу аналітичну форму).
Розрахункове значення t-критерію:
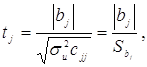
cjj – діагональний j-й елемент матриці С=![]()
![]()
Для отримання оцінок дисперсії Dj розрахуємо дисперсійно-коваріаційну матрицю (іноді її називають коваріаційною).
Розраховується вона за формулою
![]() ,
,
де ![]() - дисперсія залишків
- дисперсія залишків
Матрицю С=![]() ми маємо.
ми маємо.
![]() , де
, де
n – кількість спостережень, n=10
m – кількість оцінюваних параметрів моделі, m=4.
Стандартне відхилення залишків ![]() = 4,912352.
= 4,912352.
Отримуємо:
 =
=
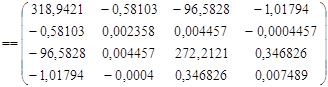
D(b0) = 318,9421,
D(b1)=0,002358,
D(b2)=272,2121,
D(b3)=0,007489
Визначимо значення стандартних помилок коефіцієнтів регресії Sbj:![]()
Sb0 = ![]() = 17,85895,
= 17,85895,
Sb1 =![]() = 0,048839,
= 0,048839,
Sb2 =![]() = 16,49885,
= 16,49885,
Sb3 =![]() = 0,086537
= 0,086537
| 17,85895 |
| 0,048839 |
| 16,49885 |
| 0,086537 |
Sb =
Розрахункове значення t-статистики отримуємо для кожного коефіцієнта:
tb0 = b0 / Sb0 = -23,83/ 17,85895 = -1,33433 і т. п.
| -1,33433 |
| 4,658181 |
| 0,546609 |
| 1,121298 |
tp =
Розрахункові значення t-статистики порівнюються за абсолютною величиною з табличним t10-4
= 1,943. Параметр вважається статистично значимим (нульова гіпотеза не підтверджується), якщо ![]()
Це означає, що в нашому випадку тільки b1 є статистично значущим і суттєво впливає на модель.
Довірчі інтервали для оцінок регресії будуються за формулою:
b0 =-23,8298±34,699 |
| b1 =0,2275±0,0949 |
| b2 =9,018423±32,0573 |
| b3 =0,097034±0,1681 |
![]() :
:
4. Якість побудованої моделі можна визначити за допомогою коефіцієнта детермінації:
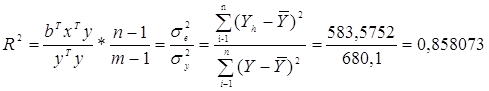 ,
,
Його значення показує, що на 85,8073% варіацію змінної Y можна пояснити варіацією пояснювальних змінних Х.
5. Тіснота зв’язку між Y і X для множинної регресії визначається за допомогою коефіцієнтів кореляції трьох типів:
- коефіцієнта множинної кореляції R (визначається як корінь з коефіцієнта детермінації) – показує тісноту зв’язку між Y і всією множиною пояснювальних зміннихX (1 на модель) ;
- парних коефіцієнтів кореляції r, що знаходяться в кореляційній матриці r* і характеризують тісноту зв’язку між Y та окремим Xj.Вони діляться на два типи:
а) парні коефіцієнти кореляції між Y та окремим Xj
б) парні коефіцієнти кореляції між окремими Xk і Xj rXkXj (їх для моделі існує m*m);
- частинних коефіцієнтів кореляції, що також характеризують тісноту зв’язку між Y та окремим Xj, але при умові, що інші незалежні змінні сталі, тобто їх варіація не впливає на залежність між Y та Х:
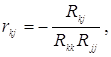
де Rkj – алгебраїчне доповнення до (j,k)-го елемента кореляційної матриці r;
Rkk та Rjj – відповідні діагональні елементи цієї матриці.
За вимогами роботи треба розрахувати коефіцієнт множинної кореляції R:
R = ![]()
де R2 – коефіцієнт детермінації;
![]() 0,926322 – тіснота зв’язку між Y і X для нашої регресії є досить великою.
0,926322 – тіснота зв’язку між Y і X для нашої регресії є досить великою.
Його значущість перевіряється також за допомогою t-статистики (нульова гіпотеза – R незначущо відрізняється від 0). В цьому випадку розрахункове значення крітерію визначається за формулою:
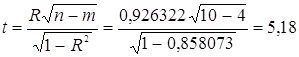
Розрахункое значення t-статистики порівнюється за абсолютною величиною з табличним t10-4 = 1,943. Оскільки розрахункове значення більше, коефіцієнт кореляції є статистично значущим.
4. Побудова прогнозу по регресійній моделі
Точковий прогноз. Задані прогнозні Х01, Х02, Х03 для певного 0-го періоду. Прогнозне значення Y0 для цього періоду розраховується по формулі:
Y0 = ![]()
Якщо Х01 = 252, Х02=0,35, а Х03 = 128 (задаються дослідником або визначаються по продовженню тенденції їх зміни), то точковий прогноз на 0-й період складе:
Y0 = ![]() = -23,83+0,23 * 252 + 9,02 0,35 + 0,10*128 = 49,07704,
= -23,83+0,23 * 252 + 9,02 0,35 + 0,10*128 = 49,07704,
чи в матричному вигляді:
Y = BТ*X0=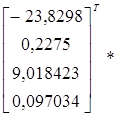
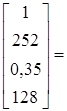 49,07704
49,07704
Де В – матриця оцінок параметрів моделі. Його стандартна похибка складає
![]() 16,60574
16,60574
Інтервальний прогноз визначається як
![]() =49,07704
=49,07704 ![]() 1,943*24,1312*
1,943*24,1312*![]() = =49,07704
= =49,07704 ![]() 11,58627
11,58627
Похожие работы
... |3121,11 |2482,57 |2505,7 |2475,59 | |ціна | | | | | | | Одиниці виміру ціни – гривні. Джерело інформації - бухгалтерський віддів ВО "Радіоприлад", Запоріжжя. Розділ 2. Оцінка регресійної моделі. Розглянемо модель залежності оптової ціни від ціни на ресурс: 1. Pопт = b0 + b1(Рресурс, де b0 та b1 – невідомі параметри моделі, Рресурс – ціна ресурсу. Оскільки ми знаємо, що нашій моделі можуть ві ...
... введемо в останню формулу її оцінку , звідки дисперсія буде: (2.2) Таким чином, середнє значення лежить у межах: (2.3) Розділ ІІІ. Лінійний регресійний аналіз інтервальних даних Перейдемо до багатомірного статистичного аналізу. Спочатку з позиції асимптотичної математичної статистики інтервальних даних розглянемо оцінки методу найменших квадратів (МНК). Статистичне дослідження ...
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
... стратегією розвитку ВАТ «Дніпропетровськгаз» є стратегія зниження мінімізації витрат, тобто зменшення собівартості реалізуємої продукції та послуг. Розділ 2. Обґрунтування заходів з підвищення економічної ефективності операційної діяльності ВАТ «Дніпропетровськгаз» 2.1 Техніко-економічне обґрунтування заходів В умовах державного регулювання цін реалізації газу єдиною стратегією розвитку ...
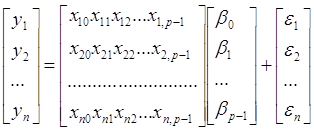

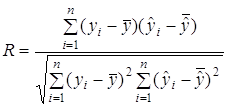
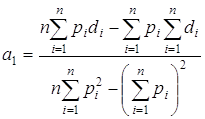
0 комментариев