Навигация
Таблица значений F-критерия Фишера для уровня значимости α = 0.05
1. Таблица значений F-критерия Фишера для уровня значимости α = 0.05
| k2\k1 | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 24 | ∞ |
| 1 | 161,45 | 199,50 | 215,72 | 224,57 | 230,17 | 233,97 | 238,89 | 243,91 | 249,04 | 254,32 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 |
| 3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 |
| 5 | 6,61 | 5,79 | 5,41 | 5, 19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3, 20 | 3,09П | 2,95 | 2,79 | 2,61 | 2,40 |
Когда m=1, выбираем 1 столбец.
k2=n-m=7-1=6 - т.е.6-я строка - берем табличное значение Фишера
Fтабл=5.99, у ср. = итого: 7
Влияние х на у - умеренное и отрицательное
ŷ - модельное значение.
| F расч. = | 28,648: 1 | = 0,92 |
| 200,50: 5 |
А = 1/7 * 398,15 * 100% = 8,1% < 10% -
приемлемое значение
Модель достаточно точная.
F расч. = 1/0,92 =1,6
F расч. = 1,6 < F табл. = 5,99
Должно быть Fрасч. > Fтабл
Нарушается данная модель, поэтому данное уравнение статистически не значимо.
Так как расчетное значение меньше табличного - незначимая модель.
| Ā ср= | 1 | Σ | (y - ŷ) | *100% |
| N | y |
Ошибка аппроксимации.
A= 1/7*0,563494* 100% = 8,04991% 8,0%
Считаем, что модель точная, если средняя ошибка аппроксимации менее 10%.
Параметрическая идентификация парной нелинейной регрессии
Модель у = а * хb - степенная функция
Чтобы применить известную формулу, необходимо логарифмировать нелинейную модель.
log у = log a + b log x
Y=C+b*X -линейная модель.
| b = |
|
|
|
![]()
![]() C=Y-b*X
C=Y-b*X
b=0.289
С = 1,7605 - ( - 0,298) * 1,7370 = 2,278
Возврат к исходной модели
Ŷ=10с*xb=102.278*x-0.298
| №п/п | У | X | Y | X | Y*X | X2 | У | I (y-ŷ) /yI |
| 1 | 68,80 | 45,10 | 1,8376 | 1,6542 | 3,039758 | 2,736378 | 60,9614643 | 0,113932 |
| 2 | 61, 20 | 59,00 | 1,7868 | 1,7709 | 3,164244 | 3,136087 | 56,2711901 | 0,080536 |
| 3 | 59,90 | 57, 20 | 1,7774 | 1,7574 | 3,123603 | 3,088455 | 56,7931534 | 0,051867 |
| 4 | 56,70 | 61,80 | 1,7536 | 1,7910 | 3,140698 | 3, 207681 | 55,4990353 | 0,021181 |
| 5 | 55,00 | 58,80 | 1,7404 | 1,7694 | 3,079464 | 3,130776 | 56,3281590 | 0,024148 |
| 6 | 54,30 | 47, 20 | 1,7348 | 1,6739 | 2,903882 | 2,801941 | 60,1402577 | 0,107555 |
| 7 | 49,30 | 55, 20 | 1,6928 | 1,7419 | 2,948688 | 3,034216 | 57,3987130 | 0,164274 |
| Итого | 405, 20 | 384,30 | 12,3234 | 12,1587 | 21,40034 | 21,13553 | 403,391973 | 0,563493 |
| Средняя | 57,88571 | 54,90 | 1,760486 | 1,736957 | 3,057191 | 3,019362 | 57,62742 | 0,080499 |
Входим в EXCEL через "Пуск"-программы. Заносим данные в таблицу. В "Сервис" - "Анализ данных" - "Регрессия" - ОК
Если в меню "Сервис" отсутствует строка "Анализ данных", то ее необходимо установить через "Сервис" - "Настройки" - "Пакет анализа данных"
Прогнозирование спроса на продукцию предприятия. Использование в MS Excel функции "Тенденция"
A - спрос на товар. B - время, дни
| № п/п | A |
|
| 1 | 11 | 1 |
| 2 | 14 | 2 |
| 3 | 13 | 3 |
| 4 | 15 | 4 |
| 5 | 17 | 5 |
| 6 | 17,9 |
|
| 7 | 18,4 | 7 |
1/3
1
Шаг 1. Подготовка исходных данных
Шаг 2. Продлеваем временную ось, ставим на 6,7 вперед; имеем право прогнозировать на 1/3 от данных.
Шаг 3. Выделим диапазон A6: A7 под будущий прогноз.
Шаг 4. Вставка функция
| Шаг1 Категория Полный алфавитный перечень Тенденция | Шаг2 Тенденция Известные значения x (курсор В1: В5) Выделяем с 1 по 5 |
| Новый x | В6: В7 |
| Известный y | А1: А5 |
| Const | 1 |
| Ок |
Шаг 5. ставим курсор в строку формул за последнюю скобку
| = ТЕНД () |
<Ctrl+Shift+Enter>
![]() Вставка диаграмма нестандартны
гладкие графики
Вставка диаграмма нестандартны
гладкие графики
диапазон у готово.
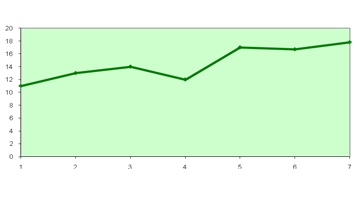
Если каждое последующее значение нашего временной оси будет отличаться не на несколько процентов, а в несколько раз, тогда нужно использовать не функцию "Тенденция", а функцию "Рост".
Список литературы
1. Елисеева "Эконометрика"
2. Елисеева "Практикум по эконометрике"
3. Карлсберг "Excel для цели анализа"
Приложение
| ВЫВОД ИТОГОВ | ||||||||
| Регистрационная статистика | ||||||||
| Множественный R | 0,947541801 | |||||||
| R-квадрат | 0,897835464 | |||||||
| Нормированный R-квадрат | 0,829725774 | |||||||
| Стандартная ошибка | 0,226013867 | |||||||
| Наблюдения | 6 | |||||||
|
|
|
|
|
|
|
|
| |
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F |
|
|
| |
| Регрессия | 2 | 1,346753196 | 0,673376598 | 13,18219855 | 0,032655042 | |||
| Остаток | 3 | 0,153246804 | 0,051082268 | |||||
| Итого | 5 | 1,5 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | Р-значение | Нижние 95% | Верхние 95% | Нижние 95% | Верхние 95% | |
| Y-пересечение | 4,736816539 | 0,651468195 | 7,27098664 | 0,005368842 | 2,66355399 | 6,810079088 | 2,66355399 | 6,810079088 |
| Переменная X1 | 0,333424008 | 0,220082134 | 1,51499807 | 0,227014505 | -0,366975566 | 1,033823582 | -0,366975566 | 1,033823582 |
| Переменная X2 | 0,077993238 | 0,038841561 | 2,007984153 | 0,138252856 | -0,045617943 | 0, 201604419 | -0,045617943 | 0, 201604419 |
Похожие работы
... ПО “Уралмаш”, “АвтоВАЗ”, МИИТ, Казахского политехнического института, Донецкого государственного университета и многих других. Затем Институт в качестве Лаборатории эконометрических исследований разрабатывал эконометрические методы анализа нечисловых данных, а также процедуры расчета и прогнозирования индекса инфляции и валового внутреннего продукта. Институт высоких статистических технологий и ...
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
... что только что проведенное сравнение ранжировок (1) и (2) осуществлено не вполне строго. Ясно, что в эконометрическом инструментарии специалиста по проведению экспертных исследований должен быть алгоритм согласования ранжировок, полученных различными методами. Метод согласования кластеризованных ранжировок Рассматриваемая здесь проблема состоит в выделении общего нестрогого порядка из набора ...
... осуществляется подстановкой в уравнение регрессии значений независимых переменных, которые определяют условия, для которых делается прогноз. 2.2 Методы планирования и прогнозирования доходов бюджетов органов местного самоуправления Методы прогнозирования и планирования выражаются в способах и приемах разработки прогнозных и плановых документов и показателей применительно к различным их видам ...
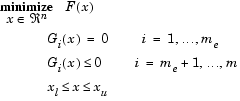
0 комментариев