I = 2

1. i = 2

2 Переносим элемент х=а_i из входной подпоследовательности в готовую так, чтобы последняя осталась под сортированной. Для этого:

а) организуем бинарный поиск места включения х в готовую подпоследовательность: находим срединный элемент готовой подпоследовательности – a_m, где m =] i/2 (, и сравниваем его с х. Если a_m > х то ведем далее поиск в левой половине готовой подпоследовательности, т.е. опять находим срединный элемент и сравниваем его с х и т.д., пока не найдем номер j такой, что a_i <=x < a_i+1, иначе аналогично ведем поиск в правой половине готовой подпоследовательности;

б) если j=j-1, то переходим к пункту в), иначе расширяем готовую подпоследовательность справа, сдвигая ее элементы, начиная с a_i вправо;

в) a_i+1 = х

3. i=i+1. Если i <= n, то переходим к п. 2, иначе сортировка заканчивается.

Деление пополам производится i*log₂i. Число сравнений практически не зависит от начального порядка элементов. В нижней части последовательности место включения отыскивается несколько быстрее, чем в верхней, поэтому предпочтительна ситуация, когда элементы немного упорядочены. Фактически, если элементы в обратном порядке, потребуется минимальное число сравнений, если уже упорядочены – максимальное:

C≈n*log₂(log₂-log₂e±0,5). Однако число пересылок так и остается порядка n². И на самом деле сортировка уже упорядоченного массива потребует больше времени, чем метод с прямыми включениями (см. [1]).

2.3 Выбор структур данных

Алгоритмы сортировки очень сильно зависят от структуры данных, так что выделяют два класса: сортировку массивов и сортировку последовательностей (файлов). В данной работе рассматривается сортировка массивов. Тип данных «массив» удобен тем, что хранится во внутренней памяти и имеет случайный доступ к элементам, то есть более быстрый, чем у последовательности. Поэтому массивы целесообразно использовать для хранения небольших, часто используемых множеств.

Обычно упорядочивающая функция не вычисляется по какому-либо правилу, а хранится как явная компонента (поле) каждого элемента. Её значение называется ключом элемента. Поэтому для представления элемента хорошо подходит тип «запись», что на языке «Pascal» выглядит следующим образом:

TYPE item = RECORD key: INTEGER;

{здесь описаны другие компоненты}

END;

Поскольку в алгоритме сортировки используется только ключ элемента, то остальную информацию об элементе можно опустить – считаем, что тип элемента определен как INTEGER. Можно выбрать и другой тип, на котором определено общее отношение порядка.

Из выше сказанного следует, что в процессе работы потребуются следующие переменные:

n – количество элементов массива;

A – сортируемый массив;

i – переменная цикла (по исходной последовательности);

j – переменная внутреннего цикла (по готовой последовательности);

x – i-й ключ (переносимый элемент).

Все переменные целого типа.

2.4 Описание схемы алгоритма

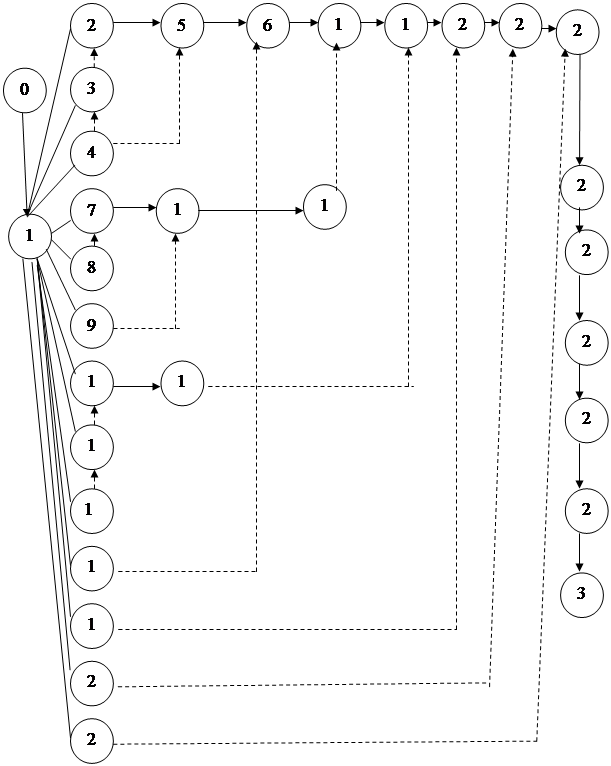
Блок-схема данного алгоритма изображена на рис. 2 в Приложении.

Алгоритм работает следующим образом. Сначала вводятся исходные данные: длина массива и его элементы (блоки 1, 2), затем организуется цикл по всей длине массива, во время которого ставится «барьер» (блок 3) и проводится сравнение i-го ключа с элементами готовой последовательности (стоящими раньше него). При этом все элементы, большие этого ключа (это условие проверяется в блоке 4), сдвигаются вправо (блок 5). Это происходит до тех пор, пока не встретится элемент меньший либо равный данному ключу (по крайней мере барьеру). Тогда i-й ключ вставляется в эту позицию (блок 6).

2.5 Контрольные примеры решения задачи с помощью алгоритма сортировки простыми включениями

Пример сортировки массива, отсортированного случайным образом.

Пусть задан такой массив из восьми элементов: (32,43,2,30,82,8,5,52) (см. Таб. 1).

Начальные ключи	32	43	02	30	82	08	05	52
i = 2	32	43	02	30	82	08	05	52
i = 3	02	32	43	30	82	08	05	52
i = 4	02	30	32	43	82	08	05	52
i = 5	02	30	32	43	82	08	05	52
i = 6	02	08	30	32	43	82	05	52
i = 7	02	05	08	30	32	43	82	52
i = 8	02	05	08	30	32	43	52	82

Пошаговое решение:

Шаг 1:

1)         i=2;

2)         x=43; a[0]=43; j=1;

3) x > a[j]=32;

3.2) a[2]= 43;

4) i=3; i ≤ n=8 → п. 2;

Шаг 2:

2) x=2; a[0]=2; j=2;

3) x < a[j]=43;

3.1) a[3]=43; j=1; → п. 3;

3) x < a[j]=32;

3.1) a[2]=32; j=0; → п. 3;

3) x = a[j];

3.2) a[1]=2;

4) i=4; i<n → п. 2;

Шаг 3:

2) x=30; a[0]=30; j=3;

3) x < a[j]=43;

3.1) a[4]=43; j=2; → п. 3;

3) x < a[j]=32;

3.1) a[3]=32; j=1; → п. 3;

3) x > a[1]=2

3.2) a[2]=30;

4) i=5; i<n → п. 2;

Шаг 4:

2) x=82; a[0]=82; j=4;

3) x > a[j];

3.2) a[5] = 82;

4) i=6; i<n → п. 2;

Шаг 5:

2) x=8; a[0]=8; j=5;

3) x < a[j]=82;

3.1) a[6]=82; j=4; → п. 3;

3) x < a[j]=43;

3.1) a[5]=43; j=3; → п. 3;

3) x < a[j]=32;

3.1) a[4]=32; j=2; → п. 3;

3) x < a[j]=30;

3.1) a[3]=30; j=1; → п. 3;

3) x > a[j]=2;

3.2) a[2]=8;

4) i=7; i<n → п. 2;

Шаг 6:

2) x=5; a[0]=5; j=6;

3) x < a[j]=82;

3.1) a[7]=82; j=5; → п. 3;

3) x < a[j];

3.1) a[6]=43; j=4; → п. 3;

3) x < a[j]=32;

3.1) a[5]=32; j=3; → п. 3;

3) x < a[j]=30;

3.1) a[4]=30; j=2; → п. 3;

3) x < a[j]=8;

3.1) a[3]=8; j=1; → п. 3;

3) x > a[j]=2;

3.2) a[2]=5;

4) i=8; i≤n → п. 2;

Шаг 7:

2) x=52; a[0]=52; j=7;

3) x < a[j]=82;

3.1) a[8]=82; j=6; → п. 3;

3) x > a[j]=43;

3.2) a[7]=52;

4) i=9; i>n → конец алгоритма.

Таким образом, имеем 21 пересылку элементов и 20 сравнений.

Пример сортировки уже отсортированного массива.

Пусть задан такой массив из восьми элементов: (2,5,8,30,32,43,52,82).

Пошаговое решение:

Шаг 1:

1) i=2;

2) x=5; a[0]=2; j=1;

3) x > a[j]=2;

3.2) a[2]=5;

4) i=3; i<n → п. 3;

Шаг 2:

2) x=8; a[0]=8; j=2;

3) x > a[j]=5;

3.2) a[3]=8;

4) i=4; i<n → п. 3;

Шаг 3:

2) x=30; a[0]=30; j=3;

3) x > a[j]=8;

3.2) a[4]=30;

4) i=5; i<n → п. 3;

Шаг 4:

2) x=32; a[0]=32; j=4;

3) x > a[j]=30;

3.2) a[5]=32;

4) i=6; i<n → п. 3;

Шаг 5:

2) x=43; a[0]=43; j=5;

3) x > a[j]=32;

3.2) a[6]=43;

4) i=7; i<n → п. 3;

Шаг 6:

2) x=52; a[0]=52; j=6;

3) x > a[j]=43;

3.2) a[7]=52;

4) i=8; i≤n → п. 3;

Шаг 7

2) x=82; a[0]=82; j=7;

3) x > a[j]=52;

3.2) a[8]=82;

4) i=9; i>n →конец алгоритма.

Таким образом получили 7 пересылок и 7 сравнений.

Пример сортировки массива, отсортированного в обратном порядке.

Пусть задан такой массив из восьми элементов: (82,52,43,32,30,8,5,2).

Пошаговое решение:

Шаг 1:

1) i=2;

2) x=52; a[0]=52; j=1;

3) x< a[j]=52;

3.1) a[2]=82; j=0; → п. 3;

3) x=a[j];

3.2) a[1]=52;

4) i=3; i<n → п. 2;

Шаг 2:

2) x=43; a[0]=43; j=2;

3) x < a[j]=82;

3.1) a[3]=82; j=1; → п. 3;

3) x < a[j]=52;

3.1) a[2]=52; j=0; → п. 3;

3) x = a[j];

3.2) a[1]=43;

4) i=4; i<n → п. 2;

Шаг 3:

2) x=32; a[0]=32; j=3;

3) x < a[j]=82;

3.1) a[4]=82; j=2; → п. 3;

3) x < a[j]=52;

3.1) a[3]=52; j=1; → п. 3;

3) x < a[j]=43;

3.1) a[2]=43; j=0; → п. 3;

3) x=a[j];

3.2) a[1]=32;

4) i=5; i<n → п. 2;

Шаг 4:

2) x=30; a[0]=30; j=4;

3) x < a[j]=82;

3.1) a[5]=82; j=3; → п. 3;

3) x < a[j]=52;

3.1) a[4]=52; j=2; → п. 3;

3) x < a[j]=43;

3.1) a[3]=43; j=1; → п. 3;

3) x < a[j]=32;

3.1) a[2]=32; j=0; → п. 3;

3) x=a[j];

3.2) a[1]=30;

4) i=6; i<n → п. 2;

Шаг 5:

2) x=8; a[0]=8; j=5;

3) x < a[j]=82;

3.1) a[6]=82; j=4; → п. 3;

3) x < a[j]=52;

3.1) a[5]=52; j=3; → п. 3;

3) x < a[j]=43;

3.1) a[4]=43; j=2; → п. 3;

3) x < a[j]=32;

3.1) a[3]=32; j=1; → п. 3;

3) x < a[j]=30;

3.1) a[2]=30; j=0; → п. 3;

3) x=a[j];

3.2) a[1]=8;

4) i=7; i<n → п. 2;

Шаг 6:

2) x=5; a[0]=5; j=6;

3) x < a[j]=82;

3.1) a[7]=82; j=5; → п. 3;

3) x < a[j]=52;

3.1) a[6]=52; j=4; → п. 3;

3) x < a[j]=43;

3.1) a[5]=43; j=3; → п. 3;

3) x < a[j]=32;

3.1) a[4]=32; j=2; → п. 3;

3) x < a[j]=30;

3.1) a[3]=30; j=1; → п. 3;

3) x < a[j]=8;

3.1) a[2]=8; j=0; → п. 3;

3) x=a[j];

3.2) a[1]=5;

4) i=8; i<n → п. 2;

Шаг 7:

2) x=2; a[0]=2; j=7;

3) x < a[j]=82;

3.1) a[8]=82; j=6; → п. 3;

3) x < a[j]=52;

3.1) a[7]=52; j=5; → п. 3;

3) x < a[j]=43;

3.1) a[6]=43; j=4; → п. 3;

3) x < a[j]=32;

3.1) a[5]=32; j=3; → п. 3;

3) x < a[j]=30;

3.1) a[4]=30; j=2; → п. 3;

3) x < a[j]=8;

3.1) a[3]=8; j=1; → п. 3;

3) x < a[j]=5;

3.1) a[2]=5; j=0; → п. 3;

3) x=a[j];

3.2) a[1]=2;

4) i=9; i>n → конец алгоритма.

Таким образом, имеем 35 сравнений и 35 пересылок.