Навигация
4.4 Контрольный пример
Для подробного описания действия волнового алгоритма поиска длиннейшего пути воспользуемся графом задаваемым таблице связностей:
| X1 | X2 | X3 | X4 | X5 | X6 | |
| X1 | 1 | 4 | ||||
| X2 | 2 | 5 | ||||
| X3 | 2 | 4 | ||||
| X4 | 1 | 4 | ||||
| X5 | 2 | |||||
| X6 |
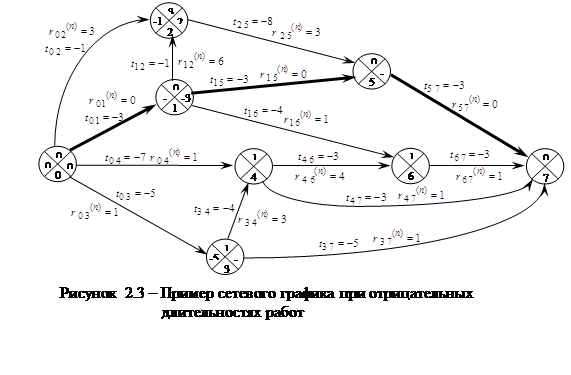
Таким образом, зная таблицу связностей можно построить граф для более наглядной иллюстрации примера:
Итак, на первом проходе волнового алгоритма выполняется пункт 1, т.е. устанавливаются значения весов всех вершин в нуль, и помещает в массив М индекс начальной вершины, математически это можно записать так:
Шаг №1:
П. 1: ![]()
На втором проходе, т. к. М<>0, выполняется пункт 2, из массива М забирается первый элемент, этот индекс присваивается индексной переменной i составляется множество исходов для вершины Х i, а затем вычисляются веса смежных вершин:
Шаг №2:
П. 2: ![]()
![]()
![]()
Как видно из приведенных записей, в результате этого прохода две вершины: вторая и третья получили новые веса, и соответственно в массив М попали их индексы, так как до этого они в нем не содержались. (В дальнейшем для краткости изложения будут приводиться преимущественно математические записи работы алгоритма).
Шаг №3:
П. 2: ![]()
![]()
![]()
Следует отметить, что в результате этого прохода вершина Х 3 не поменяла своего веса, так как уже имела максимально возможный.
Шаг №4:
П. 2: ![]()
![]()
![]()
Шаг №5:
П. 2: ![]()
![]()
![]()
Шаг №6:
П. 2: ![]()
![]()
Шаг №7:
П. 2: ![]()
Шаг №8:
П. 2: М=0, выполняется п. 3.
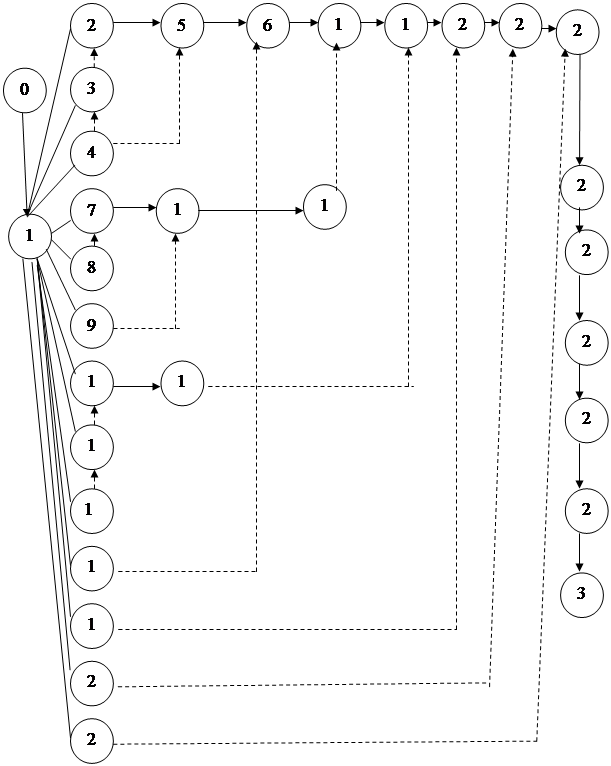
Итак, на данный момент получен граф, все вершины которого приобрели максимально возможные значения. А так как массив изменивших вес вершин пуст, то управление передается третьему пункту алгоритма, который отмечает длиннейший путь. Следует особо отметить, что, как видно из предыдущих вычислений, максимальные веса вершин могут быть достигнуты при продвижению по разным дугам. Для большей наглядности примера ниже приведен вид графа на данном этапе:
На этапе выполнения третьего пункта алгоритма критерием для выделения дуги, как и для алгоритма нахождения кратчайшего пути, является совпадение разности весов соответствующих вершин с весом самой дуги. Таким образом, начиная с вершины Х6 получим:
Шаг №9: Для выделенной вершины ![]()
П. 3: ![]()
![]() , поэтому дуга
, поэтому дуга ![]() выделяется.
выделяется.
![]() , и дуга
, и дуга ![]() выделяется, одновременно выделяются вершины
выделяется, одновременно выделяются вершины ![]() и
и ![]() .
.
Шаг №10: Для выделенной вершины ![]()
П. 3: ![]()
![]() , поэтому дуга
, поэтому дуга ![]() не выделяется.
не выделяется.
![]() , и дуга
, и дуга ![]() выделяется, одновременно
выделяется, одновременно
выделяется вершина ![]() .
.
Шаг №11: Для выделенной вершины ![]()
П. 3: ![]()
![]() , поэтому дуга
, поэтому дуга ![]() выделяется.
выделяется.
![]() , и дуга
, и дуга ![]() выделяется, одновременно выделяется вершина
выделяется, одновременно выделяется вершина ![]() , следует отметить, что вершина
, следует отметить, что вершина ![]() не выделяется, так как уже выделена.
не выделяется, так как уже выделена.
Шаг №12: Для выделенной вершины ![]()
П. 3: ![]()
![]() , поэтому дуга
, поэтому дуга ![]() не выделяется.
не выделяется.
![]() , и дуга
, и дуга ![]() выделяется, одновременно выделяется вершина
выделяется, одновременно выделяется вершина ![]() .
.
Шаг №13: Для выделенной вершины ![]()
П. 3: ![]()
![]() , и дуга
, и дуга ![]() выделяется, следует отметить, что вершина
выделяется, следует отметить, что вершина ![]() не выделяется, так как уже выделена.
не выделяется, так как уже выделена.
Шаг №14: Для выделенной вершины ![]()
П. 3: ![]()
Так как в данную вершину не входит не оной дуги и больше нет отмеченных вершин, переходим к этапу составления длиннейшего пути.
Итак соединяя дуги по принципу: конечный индекс предыдущей – начальный последующий, получаем три длиннейших путей ![]() длиной 10:
длиной 10:
1. ![]()
2. ![]()
3. ![]()
Для большей наглядности изобразим граф в своем конечном состоянии, нанеся на него значения весов вершин, веса дуг, а так же выделив длиннейшие пути и вычисление длин дуг этих путей:
Приведем табличный метод записи процесса:
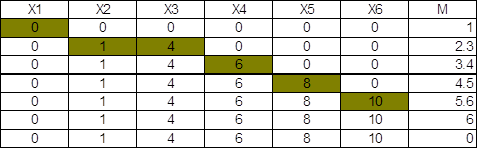
Заключение
В данной работе разработаны алгоритмы сортировки, поиска длиннейшего пути во взвешенном графе и поиска покрытия, близкого к кратчайшему. Алгоритмы исполнены с нужной степенью детализации, необходимой для понимания их работы. Рассмотрены пути улучшения эффективности каждого алгоритма учитывая требования конкретной задачи.
Большое внимание уделено сравнению возможного использования нескольких структур данных, проведён анализ эффективности работы алгоритма в зависимости от используемой структуры.
Рассмотрена сложность каждого алгоритма, её зависимость от условий данной задачи, методы упрощения и облегчения понимания алгоритма.
Похожие работы
... 6) + 1 =(509 mod 6) + 1 = 5 + 1=6; Алгоритм на графах: поиск кратчайшего пути. 3) (Y mod 5) + 1 =(509 mod 5) +1 =4 + 1 = 5; Алгоритм сортировки: сортировка-шейкер. 2 АЛГОРИТМ СОРТИРОВКИ: СОРТИРОВКА ШЕЙКЕР 2.1 Математическое описание задачи Сортировка – это перестановка элементов некоторого множества в заданном порядке при некоторой упорядочивающей функцию. Сортировка используется для ...
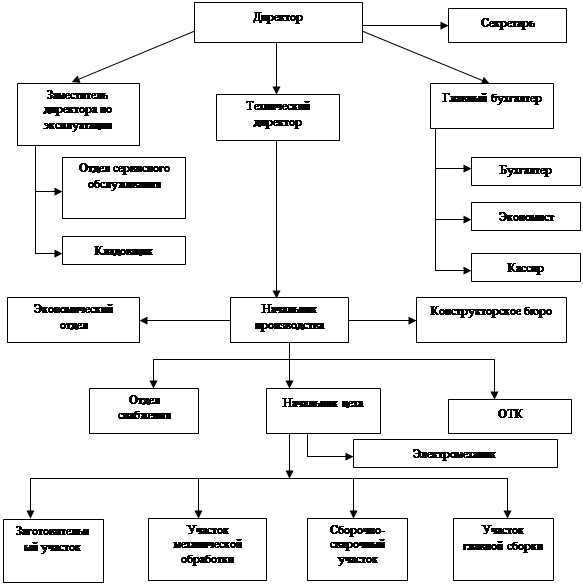
... распределения материальных благ и развития промышленного производства (сельского хозяйства, здравоохранения, связи и т. п.). Рис. 8.3. Структура системы управления общественным производством В реализации задачи инновационный менеджмент занимает специфическую и важную роль в установлении критериев и путей развития. 1 – Сбор данных и выделение ошибок. 2 – Анализ последствий ...
... телеги, микропроцессорные системы и т.д. В данном дипломном проекте поставлена задача оптимизировать сборку телеги, а также выявить экономический эффект за счет инноваций технологии и экономии ресурсов. Рассмотрим основные составляющие телеги: - Полка ТМ.201.01.03 – 24 шт. – Лист Б-О-ПН-2,0 ГОСТ 19903-74/12Х18Н10Т ГОСТ 5582-75; - Заглушка ТМ.201.01.09 – ...
... руководителя. Большое внимание следует уделять мотивации управленческого труда. 56. Организационно-распорядительные методы управления (Или административные). С их помощью осуществляются регулирующие функции гос-ва. Основаны на исполнении обязательных предписаний и рекомендаций, позволяют оперативно воздействовать на ход событий в процессе упр-я, ср-во волевого и конкретного воздействия ( ...
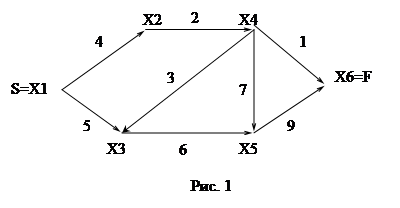



0 комментариев