Навигация
Заключение. Редакторский анализ и его значение
4. Заключение. Редакторский анализ и его значение
Редакторский анализ как профессиональный метод представляет собой комплекс специальных приемов, позволявших выполнять редакционно-издательскую работу целесообразным путем в полном объеме и с должным по качеству результатом.
Литературное произведение всегда сложное по составу. Кроме вербальной части оно может содержать и внетекстовые материалы (рисунки, формулы, таблицы). Разнообразный фактический материал произведения имеет свою природу, свои способы выражения, свою содержательную, логическую, эмоциональную, эстетическую, психологическую значимость.
Редактор, как и любой другой специалист, в своей профессиональной деятельности ориентируется на конечный продукт – издание, которое также сложное по составу и в каждом случае имеет свои особенности.
Сложность объекта деятельности обусловливает особенности методических приемов работы с ним и методики в целом. Именно специфика литературного произведения определяет такой состав элементов редакторского анализа, который позволяет всесторонне изучить и оценить литературный материал: его содержание и форму. Редакторский анализ – это синтез специально-предметного, логического к лингвостилистического анализа.
Профессиональная редакторская оценка произведения – оценка объективная. Она предполагает, во-первых, выявление как достоинств, так и недостатков произведения и, во-вторых, строгое обоснование, доказательность всех выводов.
Анализ, опенка произведения и все выводы, касавшиеся возможности публикации, могут быть правильными только тогда, когда при использовании критериев оценки темы, фактического материала, композиции, языка и стиля произведения учитываются:
1. все особенности произведения (предмета, рассматриваемого в нем, вида литературы, жанра, авторской индивидуальности);
2. особенности издания (вида, целевого назначения, читательского адреса, характера информации).
Кроме того, рассмотрение материала произведения в любом аспекте (идейно-тематическом, содержательном, композиционном, редакционно-техническом) требует учета его содержательной значимости, реальной значимости для читателя, природы фактов, средств выражения, форм представления, информативной, эмоциональной и психологической их насыщенности.
Поскольку редактор, как и любой другой специалист, в своей профессиональной деятельности ориентируется на конечный продукт, изучение, оценка и совершенствование произведения связываются также с элементами аппарата, оформлением и полиграфическим исполнением издания.
Приступая к работе с научно-популярными статьями, редактор мысленно представляет комплекс требований к научно-популярной статье и к сборнику научно-популярных статей. Анализ и опенка авторского труда дают материал, который сопоставляется с требованиями к научно-популярной статье, и на основе сравнительного анализа и можно сделать общий оценочный вывод, получилась ли научно-популярная статья или нет. А если статья не получилась, то возникает следующий вопрос: есть ли в данном случае материал, достаточный для доработки. При этом необходимо также решить, соответствует статья концепции предполагаемого издания, материал ее может быть хорошим по характеристикам вида литературы и жанра, но может не подходить для задуманного издания по тематике, предметно-проблемной направленности, объему, иллюстрированию или каким-либо другим особенностям. Редактор, используя материал про наведения, полученный в результате его изучения, обосновывает свои оценочные выводы и решение о публикации. Это обоснование позволяет утверждать, что выводы и решения редактора отвечают реальному положению дел, они свободны от личных пристрастий, вкусов и произвола редактора.
Анализируя фактологическую основу произведения, редактор в какой-то момент обращается к цифровым данным. Применительно к цифрам он использует все критерии опенки фактического материала. При атом определяет, какую роль играет этот цифровой материал в произведении в дедом и в отдельных его частях, какова его логическая содержательная значимость — в какие содержательные блоки он входит: в ключевые положения, аргументацию или примеры. Нельзя использовать критерии опенки цифрового материала без учета специфики вида литературы, к которому относится рассматриваемое произведение, специфики его жанра, полевого назначения, читательского адреса и предмета изложения. Разные требования предъявляются к цифрам, в том числе к их точности, например, в научном и научно-популярном произведении в ключевых положениях, аргументах и примерах. Целесообразная степень точности цифровых данных зависит от предмета изложения. Большой объем цифрового материала в производственно-технической книге может быть разумно-достаточным, а в научно-популярной он недопустим.
Для примера в данном случае выбран один из довольно простых вариантов работы, поскольку выделение формульного материала в произведении труда не составляет, специального анализа не требует. Способы его проверки также вполне определенны. Но и при этом анализ его чрезвычайно сложный: многоаспектный, многоплановый, многоуровневый. Когда анализируются словесно-понятийные материалы к формулам, где нужны система логических доказательств, сложная цель логических действий, где уже сама классификация фактов бывает трудной, процесс умственной работы еще более усложняется, как усложняются и задачи, которые решает редактор.
Сложна и многообразна работа редактора. Успешно справляться с ней сможет лишь тот, кто станет знатоком издательского дела, до тонкостей изучит родной язык, овладеет мастерством критического анализа текста.
Оригинал поступает для оценки редактора часто в «сыром» несовершенном виде. Задача редактора правильно оценить текстовое содержание оригинала, в случае необходимости получить подробную консультацию у специалистов в данной области знаний, изучить правильность построение текста с точки зрения стилистики русского языка, отредактировать текст и формулы, согласовав все правки с автором, и направить на вычитку оригинал уже частично размеченным к набору.
Вовремя предварительной работы в редакции в оригинале корректурными знаками шрифтовых выделений редактор показывает, каким шрифтом набрать выделяемые слова, словосочетания или фразы, заголовки в подбор, символы, а знаками передвижки текста уточняет местоположение над- и подстрочных знаков, букв, цифр.
Задача редактора – проверить, насколько тщательно сделана разметка, проследить за тем, чтобы в оригинале не остался не выделенным ни один элемент из тех, что намечены к выделению.
Особенно внимательным приходится быть редактору при работе над текстом с математическими формулами, где нередко остается незамеченным и потому неверно набирается тот или иной элемент формулы.
В данной работе рассмотрены примеры разметки, начертания и оформления текстов с математическими формулами. Такие тексты наиболее часто встречаются в научной, научно-технической, производственной и учебной литературе. При оформлении этой работы был проанализирован учебник «Алгебра и начала математического анализа» для 10-11 классов, а также использован ряд нормативной и учебной литературы: «Стандарты издательского дела», учебник по корректуре под редакцией Б.Г. Тяпкина, учебник по техническому редактированию под редакцией В.И. Рывчина, «Справочная книга редактора и корректора», «Полиграфический словарь», учебник по основам полиграфического производства (наборным процессам) и некоторые другие учебные и справочные издания.
Надеюсь, данная курсовая работа могла бы оказать некоторую помощь при редактировании, корректуре, вычитке, верстке и наборе текстов, содержащих формулы, в данном случае математические. От степени правильности разметки и оформления оригиналов формул зависит правильность работы наборщика, а, следовательно, и качество набора, соответствие его авторскому оригиналу, то есть правильность и качество данной печатной продукции.
II. Графическая часть
Приложение 1. Нумерация формул
Пример 1. Место номера при переносе формулы
|
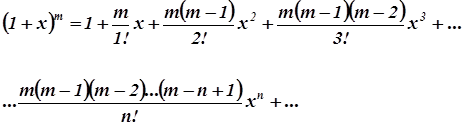
Пример 2. Нумерация группы формул, расположенных отдельными строками
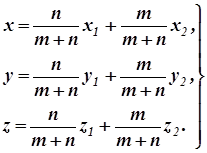 (3.4)
(3.4)
Пример 3. Нумерация группы формул — системы уравнений
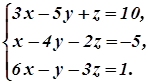 (5.6)
(5.6)
Пример 4. Нумерация формул — разновидностей основной формулы
(12а), (12б)… и т.д.
Пример 5. Нумерация промежуточных формул,
не имеющих самостоятельного значения
(а), (б), (в), (*), (**), (***) ….
Пример 6. Двойная индексационная нумерация формул
(3.7) — 7-я формула в гл. III; (9.5) — 5-я формула в § 9
Пример 7. Тройная индексационная нумерация формул
(7.9.6) — 6-я формула в § 9 гл. VII.
Приложение 2. Ссылки на номера формул в тексте
Пример 1. Основная форма ссылки
в формуле (3.4); из уравнения (15.6) вытекает и т.п.
Пример 2. Вариант ссылки без определяющего слова перед номером
Рекомендуется: Не рекомендуется:
Из формулы (7.8) следует .... Из (7.8) следует …
Пример 3. Ссылка на формулу в тексте, заключенном в скобки
Используя выражение для дивергенции [см. формулу (19.1)], получаем.....
Приложение 3. Пунктуация в тексте с формулами
Пример 1. Двоеточие перед формулой
а) … из формул сложения следуют формулы двойного аргумента:
sin 2 α = 2 sin cos α,
cos α = cos2 α – sin2 α, …
и т.д.
б) …разделив почленно последние два равенства, получим:
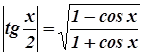
Приложение 4. Экспликация к формуле
Пример 1. Пунктуационное оформление текста с формулой и экспликацией
Индуктивность многослойной катушки определяется по формуле
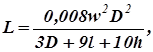
где w – число витков;
D – средний диаметр намотки, мм;
l – длина намотки, мм;
h – высота намотки, мм.
Приложение 5. Оформление записи формулы
Пример 1. Скобки
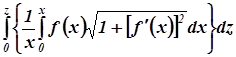
Пример 2. Скобки
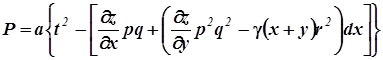
Пример 3. Скобки
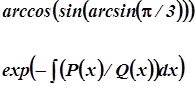
Пример 4. Коэффициенты
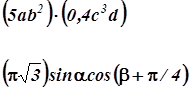
Пример 5. Употребление точки на средней линии как знака умножения
Точку ставят:
а) ![]() ;
; ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() ;
;
д) ![]() .
.
Пример 6. Употребление точки на средней линии как знака умножения
Точку не ставят:
а) ![]()
![]() ;
;
б) ![]()
в) 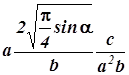 ;
;
г) ![]() ;
; 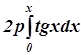 ; ab ln y.
; ab ln y.
д) ![]() .
.
Пример 7. Употребление точки на средней линии как знака умножения
Рекомендуется: Не рекомендуется:
![]()
![]()
![]()
![]()
Пример 8. Употребление косого креста как знака умножения
а) площадь комнаты: ![]()
б) ![]() .
.
Пример 9. Многоточие в ряду перечисляемых, складываемых, приравниваемых символов
a1 + а2 + ... + аn; b1 = b2 = ... = bm.
Пример 10. Многоточие между перемножаемыми символами
![]()
Пример11. Многоточие и отточие в системах уравнений, матрицах, определителях
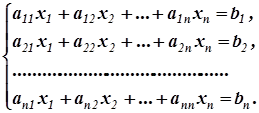
Приложение 6. Переносы в формулах
Пример 1. Перенос дроби с длинным числителем и коротким знаменателем
Дробь 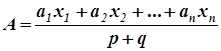 ;
;
можно привести к виду 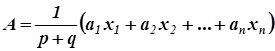
или, если использовать косую черту к виду A = (a1x1 + a2x2 + … + anxn)/(p + q)
Пример 2. Перенос дроби с коротким числителем и длинным знаменателем
Дробь ![]()
можно привести к виду, если использовать косую черту,
![]()
Пример 3. Перенос формулы с длинным подкоренным выражением, не умещающимся в формат набора
Формулу ![]()
можно записать в виде ![]()
Приложение 7. Приемы обработки формул и текста с ними, позволяющие экономить площадь бумаги
Пример 1. Перевод выражений с дробной чертой в однострочные
Формулы: 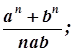
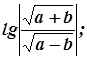
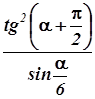
можно записать
(an + bn) / (nab); ![]() ;
; ![]()
Пример 2. Перевод выражений с дробной чертой в однострочные
Выражения:
![]()
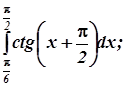
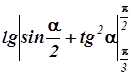
можно заменить
![]() ;
;
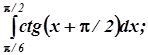
![]()
Пример 3. Запись с помощью ехр
Запись
![]()
![]()
можно представить
![]() ;
; 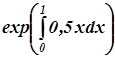
Пример 4. Свернутые формы записи обозначений
Сумму а1 + а2 + ... + аn
можно записать в виде ![]() ;
;
Произведение ![]() в виде
в виде ![]()
Последовательность a1 , a2 , … , an, … в виде ![]() .
.
Пример 5. Сокращенные формы записи матриц, определителей и систем линейных уравнений
Вместо матрицы 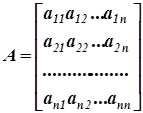
можно употребить краткую запись ![]() , 1≤ p ≤ n ; 1≤ q ≤ n
, 1≤ p ≤ n ; 1≤ q ≤ n
Пример 6. Сокращенные формы записи матриц, определителей и систем линейных уравнений
Используя такую запись, можно систему уравнений
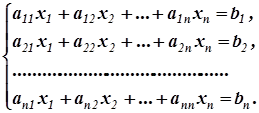
можно кратко записать в виде AX=B, ![]() , 1 ≤ k ≤ n ; 1 ≤ l ≤ n,
, 1 ≤ k ≤ n ; 1 ≤ l ≤ n,
X=(x1 , x2 , …, xn), B=(b1 , b2 , … , bn).
Пример 7. Замена однотипных формул, в которых величины изменяются по одному и тому же правилу, одним выражением
Текст
Формулы для первых четырех моментов имеют вид
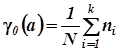 (1)
(1)
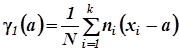 (2)
(2)
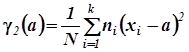 (3)
(3)
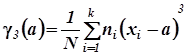 (4)
(4)
можно более компактно записать так:
Формулы для первых четырех моментов имеют вид
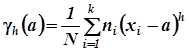 (h = 0 ; 1 ; 2 ; 3)
(h = 0 ; 1 ; 2 ; 3)
Пример 8. Расположение формул в подбор с текстом
Текст
Согласно условию, имеем Р(А) = 0,784.
Поэтому 0,784 = 1 - q3,
uли q3 =1-0,784=0,216.
Отсюда получаем ![]() .
.
Следовательно, искомая вероятность р = 1 – q = 1 - 0,6 = 0,4.
рекомендуется расположить в подбор:
Согласно условию, имеем Р(А) = 0,784. Поэтому 0,784 = 1 - q3,
или q3 =1-0,784=0,216. Отсюда получаем ![]() .
.
Следовательно, искомая вероятность р = 1 – q = 1 - 0,6 = 0,4.
Пример 9. Расположение формул одна в подбор к другой
Текст
Решая полученную систему, имеем 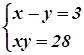
или 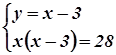
т.е. 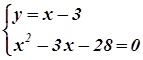
откуда x1 = 7, у1 = 4, х2 = - 4, у2 = -7.
можно расположить так:
Решая полученную систему, имеем
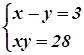 или
или 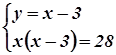 т.е.
т.е. 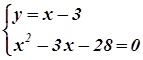 ,
,
откуда x1 = 7, у1 = 4, х2 = - 4, у2 = -7.
Возможна и такая запись:
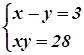 <=>
<=> 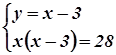 <=>
<=> 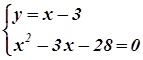 <=> (x1 = 7, у1 = 4)
<=> (x1 = 7, у1 = 4)
(х2 = - 4, у2 = -7)
Пример 10. Расположение формул одна в подбор другой
Например, в тексте
Прямоугольные и сферические координаты точки связаны соотношениями
x = q sin Θ cos φ
y = q sin φ cos Θ
z = q cos Θ .
правильнее записать все формулы в строку:
x = q sin Θ cos φ , y = q sin φ cos Θ , z = q cos Θ .
Пример 11. Расположение формул одна в подбор к другой
Например, текст
Координаты центра тяжести дуги находят по формулам
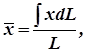 (1)
(1)
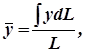 (2)
(2)
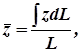 (3)
(3)
необходимо расположить следующим образом:
Координаты центра тяжести дуги находят по формулам
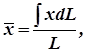
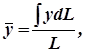
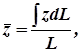 (1)
(1)
![]() Вместо ряда формул
Вместо ряда формул
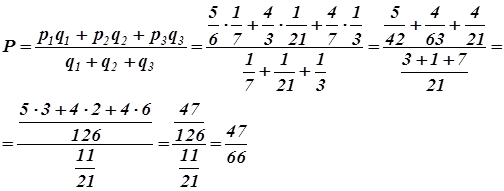
следует записать:
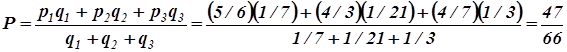 .
.
Пример 13. Замена громоздких выражений символами
Текст
Докажем, что ![]()
Оценим выражение ![]()
Так как ![]() > 0, то 0 <
> 0, то 0 < ![]() <
<![]() 0 <
0 < ![]() <
<![]()
Можно записать так:
Докажем, что A1 – A2 = α , где A1 = ![]() A2 =
A2 = ![]()
Оценим выражение A1 – A2 = α.
Так как cos α / ( 1 – sin α ) > 0, то 0< A1 < π / 2 и 0< A2 < π / 2 .
Пример 14. Преобразование текста с целью компактного размещения формул
Текст
Умножив 1-ю строку матрицы
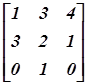
на 3-ю и вычитая ее из 2-ой строки, получаем
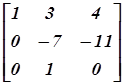
Переставив теперь 2-й и 3-й столбцы, имеем
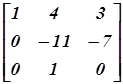
можно более компактно записать так:
Выполним над матрицей следующие преобразования:
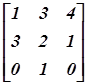
![]()
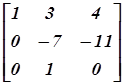
![]()
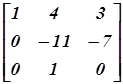
Мы умножили 1-ю строку на 3-ю и вычли ее из 2-й, а затем переставили 2-й и 3-й столбцы.
Пример 15. Перевод текста в таблицу
Текст
1. Если С=0, то уравнение принимает вид Ах + Ву = 0. Это уравнение прямой, проходящей через начало координат.
2. Если А=0, то уравнение имеет вид у = -С / В или у = b и выражает уравнение прямой, параллельной оси O x.
3. Если В=0, то уравнение имеет вид x = - C / А или x = а и выражает уравнение прямой, параллельной оси O y.
4. Если А=С=0, то уравнение примет вид у = 0. Это – уравнение оси O x.
5. Если В=С=0, то уравнение примет вид x= 0. Это – уравнение оси О y.
можно перевести в следующую таблицу
| № п/п | Значения коэффициентов | Уравнение прямой | Положение прямой |
| 1. | С=0 | А x + В y = 0 | Проходит через начало координат |
| 2. | А=0 | y = -С/В = b | Параллельна оси O x |
| 3. | В=0 | x = -С/А = а | Параллельна оси О у |
| 4. | А = С = 0 | у=0 | Совпадает с осью O x |
| 5. | В = С = 0 | x=0 | Совпадает с осью O y |
Пример 17. Использование современной символики
Текст
Если p принадлежит α, то α и p параллельны. Пусть р не принадлежит α. Проведем плоскость β, которая содержит линию пересечения прямых b и q. Так как q принадлежит α (по условию) и q принадлежит β (по построению), то q есть прямая пересечения плоскостей α и β. Допустим, что теорема неверна, т. e. р не параллельна α. Тогда существует точка С пересечения прямой р с плоскостью α.
с помощью использования математической символики примет такой вид:
Если ![]() , то p α . Пусть
, то p α . Пусть ![]() . Проведем
. Проведем ![]() . Так как
. Так как ![]() (по условию) и
(по условию) и ![]() (по построению), то
(по построению), то ![]() . Допустим,
что теорема неверна, т. е. p α. Тогда
. Допустим,
что теорема неверна, т. е. p α. Тогда ![]() .
.
Приложение 8. Разметка формул
Пример 1. Указания о переносах и отбивках
а) между символическим обозначением функции и аргументом:
sin x ; ln y ;
б) между подынтегральной функцией и дифференциалом
![]() x dx ;
x dx ; ![]() dx .
dx .
III. Список использованной литературы
Стандарты по издательскому делу / Сост. А..А. Джиго, С.Ю, Калинин. – М.: Юристъ, 1998. Рывчин В.И., Леонардова Е.И., Овчинников А. И. Техническое редактирование/ Под. ред. В.И. Рывчина. – М.: Книга, 1977. Тяпкин Б.Г., Рябинина Н.З., Баженова Л.Н. и др. Корректура / Под. ред. Б.Г. Тяпкина. – М.: Книга, 1977. Гиленсон П.Г. Справочник художественного и технического редакторов. – М.: Книга, 1988. Справочная книга редактора и корректора: Редакционно-техническое оформление издания / Сост. и общ. ред. А.Э. Мильчин. – 2-е изд., перераб. – М.: Книга, 1985. Алгебра и начало анализа: Учебник для 10-11 кл. сред. шк./А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудинцын и др.; Под. ред. А.Н. Колмогорова. – 3-е изд. – М.: Просвещение, 1993. Скорский Н.М. Теория и практика редактирования: Учебник для вузов. – 2-е изд., испр. и доп. – М.: Высш. Школа, 1980. Настольная книга издателя / Е.В. Малышкин, А.Э. Мильчин, А.А. Павлов, А.Е. Шадрин. М.: ООО «Издательство АСТ»; ООО «Агенство «КРПА Олимп», 2004. Мильчин А.Э. Культура издания, или Как надо и как не надо делать книги: Практическое руководство. – М.: Логос, 2002.Оглавление
I. Пояснительная записка ...............................................………………………...………5
1. Введение. Задачи и функции редактора ……………………………..…….5
2.Основная часть. Математические формулы…………………………….….8
2.1 Расположение формул ………………………………………………….8
2.2 Нумерация формул …………………………………………………….9
2.3 Ссылки на номера формул в тексте ………………………………….10
2.4 Пунктуация в тексте с формулами ……………………………………11
2.5 Экспликация к формуле ……………………………………………………….11
2.6 Оформление записи формулы …………………………………………………12
2.7 Переносы в формулах ………………………………………………………….13
2.8 Приемы обработки формул и текста с ними, позволяющие экономить площадь бумаги ……………………………………………………………….14
2.9 Разметка формул ………………………………………………………………16
3. Редакционно-издательский процесс ……………………………………………..17
4. Заключение. Редакторский анализ и его значение………………………………19
II. Графическая часть ……………………………………………..……………….22
Приложение 1. Нумерация формул …………………………………..……..22
Приложение 2. Ссылки на номера формул в тексте ………………..……..23
Приложение 3. Пунктуация в тексте с формулами …………………..…….24
Приложение 4. Экспликация к формуле ……………………………..……..24
Приложение 5. Оформление записи формулы ……………………………..……....25
Приложение 6. Переносы в формулах ………………………..…………..…28
Приложение 7. Приемы обработки формул и текста с ними, позволяющие экономить площадь бумаги ……………………………...…………29
Приложение 8. Разметка формул …………………………………………….36
III. Список использованной литературы ......................................………………..37
Похожие работы
... ; нажать левую кнопку мыши и, не отпуская эту кнопку, переместить указатель мыши в позицию, начиная с которой требуется поместить фрагмент. Повторение и отмена выполненных действий. Работая в редакторе Word, пользователь имеет возможность отменить или повторить последние выполненные действия. Отмена осуществляется с помощью команды Правка-Отменить и начинается с последнего действия в обратном ...
... → Свойства таблицы → Столбец (строка) → Ширина (высота) →Следующий столбец (Строка) и т.д. 2.3 Фиксация ширины столбца В новых версиях текстового редактора Word при работе с таблицей по умолчанию ширина столбца увеличивается в соответствии с содержимым, это не всегда удобно. Для фиксации ширины столбца необходимо выполнить следующее: Таблица → Автоподбор &# ...
... том виде, в каком он выйдет из печати. Кроме того, он дает возможность отобразить сразу все страницы, что удобно для внесения изменений перед распечаткой. Специальные возможности текстовых редакторов: 1) редактирование текста · работа с участком текста - выделение - удаление - запись в буфер - копирование - запись в виде отдельного файла и т.д. · выравнивание текста - по краю ( ...
... и даже стилистики при вводе документа, автоматическая коррекция наиболее часто повторяющихся ошибок, возможность автоматизации ввода повторяющихся и стандартных элементов текста, удобные механизмы работы со ссылками, сносками, колонтитулами; возможность включения в текст элементов, созданных в других программах; работа с математическими формулами; возможность автоматического создания указателей и ...
0 комментариев