Навигация
Характеристики и показатели надёжности двигателей легковых автомобилей “Merсedes”
1.6 Характеристики и показатели надёжности двигателей легковых автомобилей “Merсedes”
Таблица №
Среднее количество возникших отказов двигателей Mersedes в %
| Количество лет эксплуатации | |||||
| 3 | 5 | 7 | 9 | 11 | |
| Процент отказов | 1,5 | 2,2 | 2,5 | 2,5 | 2,6 |
2. Разработка вероятностной математической модели распределения случайных величин по значениям показателя надежности
2.1 Построение интервального вариационного ряда случайных величин
Основной целью ТЭА снижение затрат на поддержание работоспособности автомобиля в заданных эксплуатационных условиях. Наиболее эффективному решению данной задачи способствует проведение экспериментальных исследований. Это позволяет получить достоверную информацию о параметрах технического состояния автомобиля, их надежности (т.е. о ресурсах агрегатов, узлов, деталей, межремонтных пробегах и т.п.), о фактическом расходовании материальных ресурсов и трудовых затратах на производство технического обслуживания (ТО) и ремонта. Под экспериментальными исследованиями понимается как постановка специальных экспериментов – стендовых, дорожных, полигонных, когда исследователь организует и влияет на ход эксперимента, задавая различные нагрузки, режимы и т.п., так и подконтрольная эксплуатация автомобилей, выполняющих обычную транспортную работу, фиксируется и накапливается информация о всех отказах и неисправностях, пробегах нагрузках, ремонтах и т.п., а также сбор статистических данных на основании различных отчетных документов по расходу запасных частей и эксплуатационных материалов, заявки на текущий ремонт и т.д.
Одной из важных особенностей практически всех показателей и характеристик процессов ТЭА является их формирование под влиянием многих переменных факторов, точное значение которых часто неизвестно. Это так называемые вероятностные процессы. Поэтому о конкретных значениях показателей, получаемых в результате проведения эксперимента, можно говорить лишь с определенной вероятностью, а сами показатели являются случайными величинами. В этой связи с целью их изучения используется математический аппарат прикладной статистики и теории вероятностей.
Особое значение в предварительной обработке результатов эксперимента имеет анализ грубых, резко выделяющихся значений, т.е. анализ однородности экспериментального распределения. Проверим однородность экспериментальных данных по критерию Романовского.
Расположим члены выборки Xi в порядке возрастания.
Таблица 1.
Исходный вариационный ряд.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Xi | 10,0 | 10,2 | 10,3 | 10,8 | 11,5 | 12,0 | 13,3 | 13,5 | 13,8 | 14,0 | 14,2 | 14,2 | 14,3 | 14,4 |
| i | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| Xi | 14,5 | 14,6 | 14,8 | 14,8 | 14,9 | 15,0 | 15,1 | 15,1 | 15,2 | 15,3 | 15,4 | 15,5 | 15,6 | 15,7 |
| i | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
| Xi | 15,8 | 15,9 | 16,0 | 16,2 | 16,5 | 16,8 | 17,2 | 17,5 | 18,0 | 18,4 | 19,0 | 19,5 | 19,9 | 20,2 |
Результаты эксперимента должны отвечать трем основным статистическим требованиям:
- эффективности оценок, т.е. минимуму дисперсии отклонения неизвестного параметра;
- состоятельности оценок, т.е. при увеличении числа (объема) экспериментальных данных оценка параметра должна стремится к его истинному значению;
- несмещенности оценок, т.е. должны отсутствовать систематические ошибки в процессе вычисления параметров.
Для обеспечения указанных требований, а также для того, чтобы экспериментальные исследования соответствовали заданной точности и достоверности, необходимо определить минимальный, но достаточный объем Nmin экспериментальных данных, при котором исследователь может быть уверен в положительном исходе.
На основании результатов экспериментальных данных Xi вычислим:
- среднее значение ![]() :
:
![]() ;
;
- среднее квадратичное отклонение:
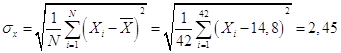 ;
;
- коэффициент вариации:
![]() ,
,
который характеризует относительную меру рассеивания Xi вокруг ![]() ;
;
- размах вариации, характеризующий абсолютную величину рассеивания результатов эксперимента:
![]() ,
,
где ![]() - соответственно максимальное и минимальное значение результатов эксперимента.
- соответственно максимальное и минимальное значение результатов эксперимента.
Принимаем ![]() и выбираем из таблицы значение критерия Стьюдента для оценки односторонней доверительной вероятности, т.е.
и выбираем из таблицы значение критерия Стьюдента для оценки односторонней доверительной вероятности, т.е. ![]() .
.
Вычисляем предельную абсолютную погрешность интервальной оценки математического ожидания:
![]() .
.
Значение ![]() характеризует абсолютную точность проведенного эксперимента и численно равно половине ширины доверительного интервала, т.е. принимаем значение t для
характеризует абсолютную точность проведенного эксперимента и численно равно половине ширины доверительного интервала, т.е. принимаем значение t для ![]() .
.
Вычислим относительную точность ![]() интервальной оценки M(X):
интервальной оценки M(X):
![]() ,
,
которая характеризует относительную ширину (в долях от ![]() ) половины доверительного интервала. Рекомендуется принимать значение
) половины доверительного интервала. Рекомендуется принимать значение ![]() = 0,05…0,15. Это значит, что половина ширины доверительного интервала для M(X) будет в пределах 5… 15% от X.
= 0,05…0,15. Это значит, что половина ширины доверительного интервала для M(X) будет в пределах 5… 15% от X.
Требуемый минимальный объем экспериментальных данных для достижения заданных ![]() :
:
![]() .
.
Применяя формулу Стеджарса, находим приближенную ширину итервала:
![]() .
.
Принимаем ![]() .
.
Определяем число интервалов группирования экспериментальных данных:
![]() .
.
Принимаем число интервалов r = 7.
0 комментариев