Навигация
Расчет числовых характеристик распределения случайных величин
2.2 Расчет числовых характеристик распределения случайных величин
Более полное, а главное, обобщенное представление о результатах эксперимента дают не абсолютные, а относительные (удельные) значения
Полученных данных. Так, вместо абсолютных значений числа экспериментальных данных ni, целесообразно подсчитать долю рассматриваемых событий в интервале, приходящихся на одно изделие (деталь, узел, агрегат или автомобиль) из числа находящихся под наблюдением, т.е. на единицу выборки. Эта характеристика экспериментального распределения называется относительной частотой (частостью) mi появления данного события (значений признака Xi):
![]() .
.
Относительная частота mi при этом, в соответствии с законом больших чисел, является приближенной экспериментальной оценкой вероятности появления события ![]() .
.
Значения экспериментальных точек интегральной функции распределения ![]() рассчитывают как сумму накопленных частостей mi в каждом интервале ri. В первом интервале
рассчитывают как сумму накопленных частостей mi в каждом интервале ri. В первом интервале ![]() во втором интервале
во втором интервале
![]() и т.д.,
и т.д.,
т.е. 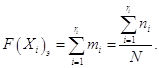
Таким образом, значение ![]() изменяются в интервале [0;1] и однозначно определяют распределение относительных частот в интервальном вариационном ряду.
изменяются в интервале [0;1] и однозначно определяют распределение относительных частот в интервальном вариационном ряду.
Другим удельным показателем экспериментального распределения является дифференциальная функция ![]() , определяемая как отношение частости
, определяемая как отношение частости ![]() к длине интервала
к длине интервала ![]()
![]()
и характеризующая долю рассматриваемых событий в интервале, приходящуюся на одно испытываемое изделие и на величину ширины интервала. Функция ![]() также еще называется плотностью вероятности распределения.
также еще называется плотностью вероятности распределения.
Полученные результаты расчета сводим в статистическую таблицу.
Таблица 2
Результаты интервальной обработки экспериментальных данных.
| Наименование параметра | Обозна- чение | Номер интервала, Ki | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Границы интервала | [a;b] | 10,0; 11,5 | 11,5 ;13,0 | 13,0; 14,5 | 14,5; 16,0 | 16,0; 17,5 | 17,5; 19,0 | 19,0; 20,5 |
| Середины интервалов |
| 10,75 | 12,25 | 13,75 | 15,25 | 16,75 | 18,25 | 19,75 |
| Опытные числа попадания в интервалы | mi | 4 | 2 | 8 | 16 | 5 | 4 | 3 |
| Опытные частоты попадания в интервал |
| 0,095 | 0,048 | 0,19 | 0,381 | 0,119 | 0,095 | 0,071 |
| Накопленная частота |
| 4 | 6 | 14 | 30 | 35 | 39 | 42 |
| Дифференциальная функция |
| 0,0635 | 0,0318 | 0,127 | 0,254 | 0,079 | 0,0635 | 0,0476 |
| Интегральная функция |
| 0,095 | 0,143 | 0,333 | 0,714 | 0,833 | 0,929 | 1 |
2.3 Анализ физических закономерностей формирования распределения случайных величин по значениям продолжительности проверки крепления стартера на автомобиле
Нормальное распределение.
Нормальное распределение, называемое также законом Гуса, находит широкое применение при исследовании эффективности функционирования транспортных средств и систем.
Теоретическим обоснованием широкого применения этого закона служит центральная предельная теорема (теорема Ляпунова А.М.), согласно которой распределение суммы независимых или слабо зависимых случайных величин, имеющих конечные математические ожидания и дисперсии одного порядка, при увеличении числа слагаемых всё меньше отличаются от нормального закона. При этом складываемые законы могут быть одинаковыми и разными.
Плотность распределения нормального закона имеет следующий вид:
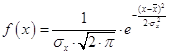 ,
,
где ![]() - математическое ожидание;
- математическое ожидание;
![]() - среднее квадратичное отклонение.
- среднее квадратичное отклонение.
Функция распределения нормального закона имеет вид:
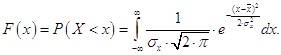
Вероятность попадания в интервал a, b случайной величины, распределенной нормально, определяется с помощью табличной функции Лапласа Ф0:
![]()
Логарифмически – нормальное распределение.
В этом случае нормальное распределение имеет не сама величина, а значение ее логарифма. Логарифмически-нормальное распределение формируется в случае, если на протекание исследуемого процесса и его результата влияет сравнительно большое число случайных и взаимно независимых величин, интенсивность действия которых зависит от достигнутого случайной величиной состояния.
Модель формирования называется моделью “пропорционального эффекта”. Данным законом хорошо описывать изменение геометрических, диагностических параметров, а так же для описания усталостных процессов, коррозии, наработки крепежных соединений.
В решении задач ТЭА Vx=0.3…0.7
Данное распределение описывает произведение воздействий случайных величин.
Дифференциальная функция логарифмически-нормального закона имеет вид:
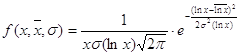
где ![]() -случайная величина, логарифм которой распределен нормально;
-случайная величина, логарифм которой распределен нормально;
![]() -математическое ожидание логарифма случайной величины;
-математическое ожидание логарифма случайной величины;
![]() -среднее квадратическое отклонение логарифма случайной величины
-среднее квадратическое отклонение логарифма случайной величины
Интегральная функция логарифмически-нормального распределения ![]() определяется следующим образом:
определяется следующим образом:
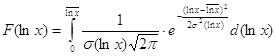
0 комментариев