Навигация
2.4. Фазовая скорость
Фазовая скорость и волны есть скорость распространения точек одинаковой фазы:
![]()
Эта скорость равна скорости гармонической волны. Фазовая скорость:
u=![]() /k=
/k=![]()
![]()
k=2![]() т.е.u=
т.е.u=![]()
| |
|
| ||||
![]() t-kx-
t-kx-![]() =const дифференцируем
=const дифференцируем
|
|
![]()
![]()
![]()
![]()
|
|
|
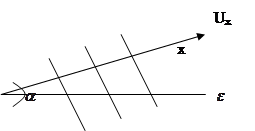
UЕ=Ux/cos![]() т.е. т.к. cos
т.е. т.к. cos![]() <1,.
<1,.
то фазовая скорость может превышать скорости света
Элементы векторного анализаНеобходимо уметь анализировать не только скалярные, но и векторные функции точки.Скалярные функции: температура неравномерно нагретого тела, плотность неоднородного тела и т. д.Векторные функции: скорость частиц текущей жидкости, сила земного притяжения, магнитное и электрическое напряжение электрического поля.Рассмотрение скалярных и векторных функций точки привело к построению теории поля.
Векторное поле а(М) называется дифференцируемым в точке М, если оно определено в окрестности точки М и если приращение ∆a=a(M’)-a(M) поля может быть представлено в виде:
∆a=А(∆r)+E(∆r);
∆r=MM’; A и E – линейные операторы;
А – не зависит от ∆r; E зависит, при ∆r=0 E=0;
Необходимое и достаточное условие дифференцируемости векторного поля а заключается в дифференцируемости его координат P, Q, R. При этом линейный оператор А изображается матрицей:
![]()
![]() дР/дх, дР/ду, дР/дz
дР/дх, дР/ду, дР/дz
А= дQ/дх, дQ/ду, дQ/дz
дR/дх, дR/ду, дR/дz
и вектор-функция А(∆r) имеет вид:
A(∆r)=1/2{A(∆r)+A*(∆r)}+1/2[pA(r)].
ДивергенцияСумма диагональных элементов матрицы, представляющей симметричную линейную вектор-функцию ½{A(∆r)+A*(∆r)} не зависит от выбора системы координат: она называется дивергенцией (расхождением) векторного поля а и обозначается diva:
diva=дP/дх+дQ/ду+дR/дz.
Вектор Р называется вихрем (ротором) поля а и записывается в виде:
rota=(дR/ду-дQ/дz ,дР/дz-Rд/дх, дQ/дх-дР/ду );
Если V поле скоростей текущей жидкости и rotV≠0, то частица движется по замкнутым линиям (образуются вихри). divV в этом случае характеризует интенсивность источника divV>0 и стока divV<0, находящегося в этой точке или отсутствие источника и стока.
Сегодня общепринято представлять уравнения Максвелла в векторной форме. Описания в декартовых координатах менее информативно.
Мы в основном будем пользоваться следующимиобозначениями:
1.Всегда используется правая системакоординат: т.е. такая вкоторой положительная ось Х совмещается с осью У,если наблюдатель смотрит вдоль положительного направления оси Z.
2.Векторы обозначаются буквами:
Е – жирный шрифт – вектор;
Е – его модуль
е – единичный вектор в направлении вектора Е.
Амплитуда вектора, который изменяется по синусоиде, обозначается символом с индексом:
Е=еЕ
и (5)
Е=Ео ехрi(wt-xz).
3.Произведение двух векторов Е и Н записывается
- скалярное произведение модуль котрого равен ЕНcos q ![]() Е
Е![]() Н
Н
- векторное произведение, модуль которого равен ЕНsinq ![]() E
E![]() H,
H,
Вращение от Е к Н происходит по часовой стрелке, если смотреть по направлению векторного произведения.
4. i,j,k – символы обозначающие единичные векторы OX, OY,OZ.
Дифференциальный векторный оператор (набла):
Ñ=i¶/¶x+j¶/¶y+k¶/¶z;(2) (6)
5.Градиент скалярной функции V определяется следующим образом:
gradV=i¶V/¶x+j¶V/¶y+k¶V/¶z; (7)
V – скалярная величина
gradV – вектор, который может меняться от точки к точке как по величине, так и по направлению.
6.Компоненты вектора Е по осям координат координат обозначаются Ex, Ey, Ez, т.е.
E=iEx+jEykEz (8)
7.Дивергенция векторной функции Е определяется как
divE=ÑE= ¶Ex/¶x+¶Ey/¶y+¶Ez/¶z; (9)
Дивергенция вектора Е – это скалярная величина.
Вихрь. Вихрь вектора E – это векторная величина
rotE=ÑxE=i (¶Ez/¶y-¶Ey/¶z)+j (¶Ex/¶z-¶Ez/¶x)+k (¶Ey/¶x-¶Ex/¶y); (10)
иногда пишут curlE вместо rotЕ.
Дивергенция представима в виде суммы следующих скалярных проезведений:
divE=i![]() ¶E/¶x+j
¶E/¶x+j![]() ¶E/¶y+k
¶E/¶y+k![]() ¶E/¶z (11)
¶E/¶z (11)
8.Вихрь представим в виде суммы следующих векторных произведений:
rotE= i![]() (¶E/¶x)+j
(¶E/¶x)+j![]() (¶E/¶y)+k
(¶E/¶y)+k![]() (¶E/¶z)
(¶E/¶z)
Оператор Лапласа:
D= ¶2/¶x2+¶2/¶y2+¶2/¶z2
Для скалярной функции ¦
D¦=¶2¦/¶x2+¶2¦/¶y2+¶2¦/¶z2
Для вектора Е
DЕ=¶2Е/¶x2+¶2Е/¶y2+¶2Е/¶z2
Е=iEx+jEy+kEz
DЕ=iDЕx+jDЕy+kDЕz.
Вихрь (ротор) – это векторная функция, компоненты которой по осям x,y,z равны соответственно:
(¶Ez/¶y-¶Ey/¶z); (¶Ex/¶z-¶Ez/¶x); (¶Ey/¶x-¶Ex/¶y)
Эта запись циклическая перестановка индексов.
9.Применения оператора Ñ2 к скаляру V означает
Ñ2V=Ñ*ÑV= div(gradV)= ¶2V/¶x2+¶2V/¶y2+¶2V/¶z2; (12)
Ñ2V – скаляр.
10.Применение оператора Ñ2 к вектору Е означает
Ñ2Е=iÑ2Ex+jÑ2Ey+kÑ2Ez=i(¶2Ex/¶x2+¶2Ey/¶y2+¶2Ez/¶z2)+
+j(¶2Ex/¶x2+¶2Ey/¶y2+ ¶2Ez/¶z2)+k(¶2Ex/¶x2+¶2Ey/¶y2+¶2Ez/¶z2); (13)
ЛИТЕРАТУРА
1. Гурский Л.И., Зеленин В.А., Жебин А.П., Вахрин Г.Л. Структура, топология и свойства пленочных резисторов.—Мн.: Навука i тэхнiка, 2007 -- 250 с.
2. Гурский Л.И., Румак Н.В., Куксо В.В. Зарядовые свойства МОП-структур.—Мн.: Навука i тэхнiка, 2000 -- 200 с.
3. Мищенко В.А., Городецкий Л.М., Гурский Л.И. и др. Интеллектуальные системы автоматизированного проектирования БИС и СБИС. Мн.: Радио и связь -- 2005. - 450 с.
Похожие работы
... энергии одного электрона на их максимальное число, соответствующее определенному энергетическому уровню. Таким образом, мы выходим на представление о существовании в каждом атоме одной или нескольких изоэнергетических поверхностей, которые следует отнести к наиболее сохраняющимся физическим величинам. По всей видимости, эта новая не совсем привычная величина определяет те внешние пространственные ...
... связано с появлением вероятностного мышления, теории относительности, принципа многозначных зависимостей. В рамках преодоления линейного подхода находятся социально-философские концепции XX в. с различными критериями членения исторического процесса. П. Сорокин признавал всеобщую реальность, проявляющуюся в многообразных материально-духовных формах. Исторический процесс, в концеп ции Сорокина, ...
... q расстояние между линиями увеличивается. Это обстоятельство в дальнейшем будет для нас существенно. Лекция 4 25 Лекция 4 4. Законы геометрической оптики 4.1. Прямолинейность распространения света. Принцип Ферма Физика в разных своих разделах часто занимается вопросами весьма несхожими. В частности оптика никак не представляется логическим продолжением предыдущих разделов, которыми мы с Вами ...
... (7.2.15.) Поскольку в рассматриваемой задаче рассматривается только один источник, то учитываем только волну с амплитудой А. В пространстве имеются 2 взаимно перпендикулярных поля ( Е и Н). Как определить направление переноса энергии ? Пср = ...
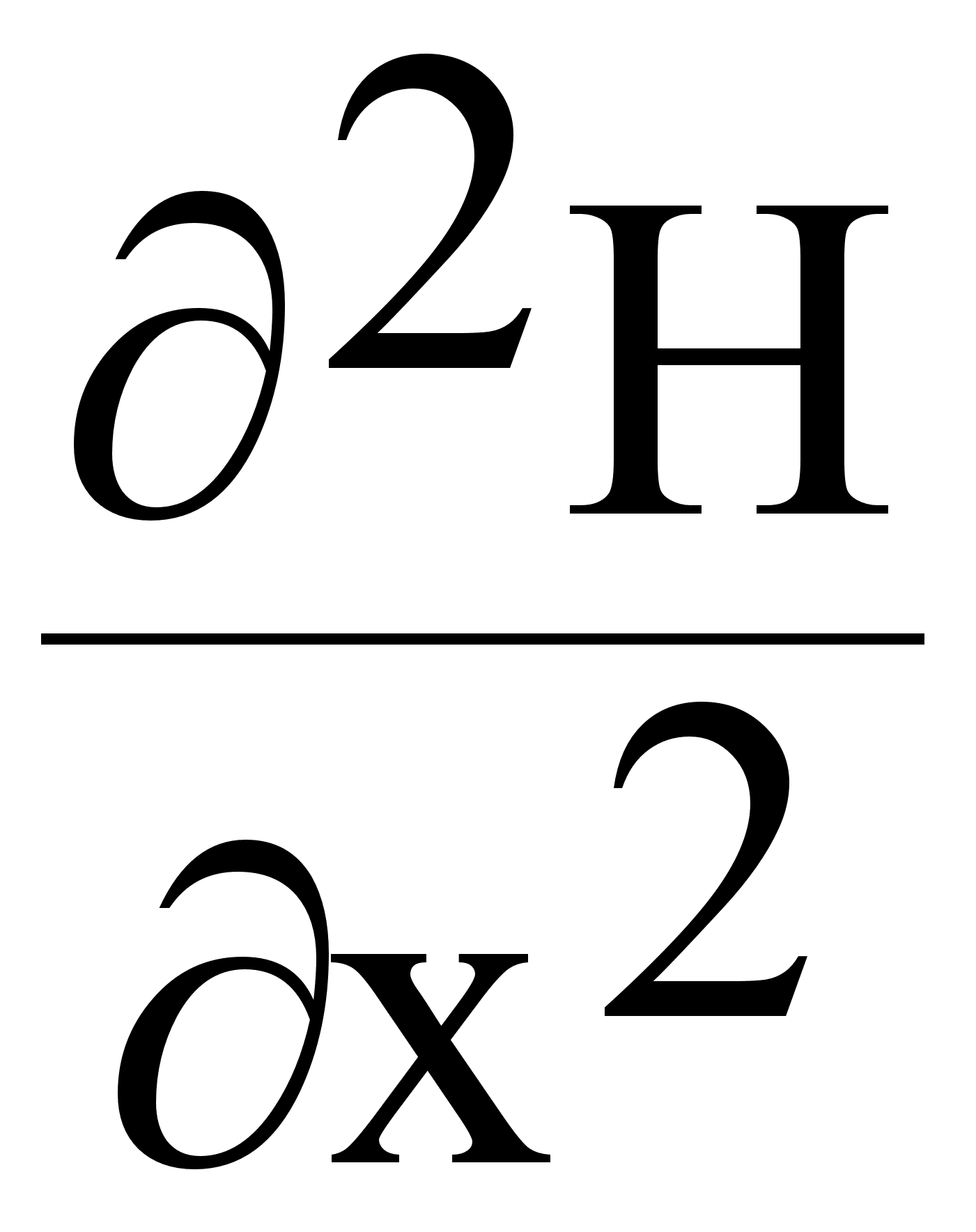
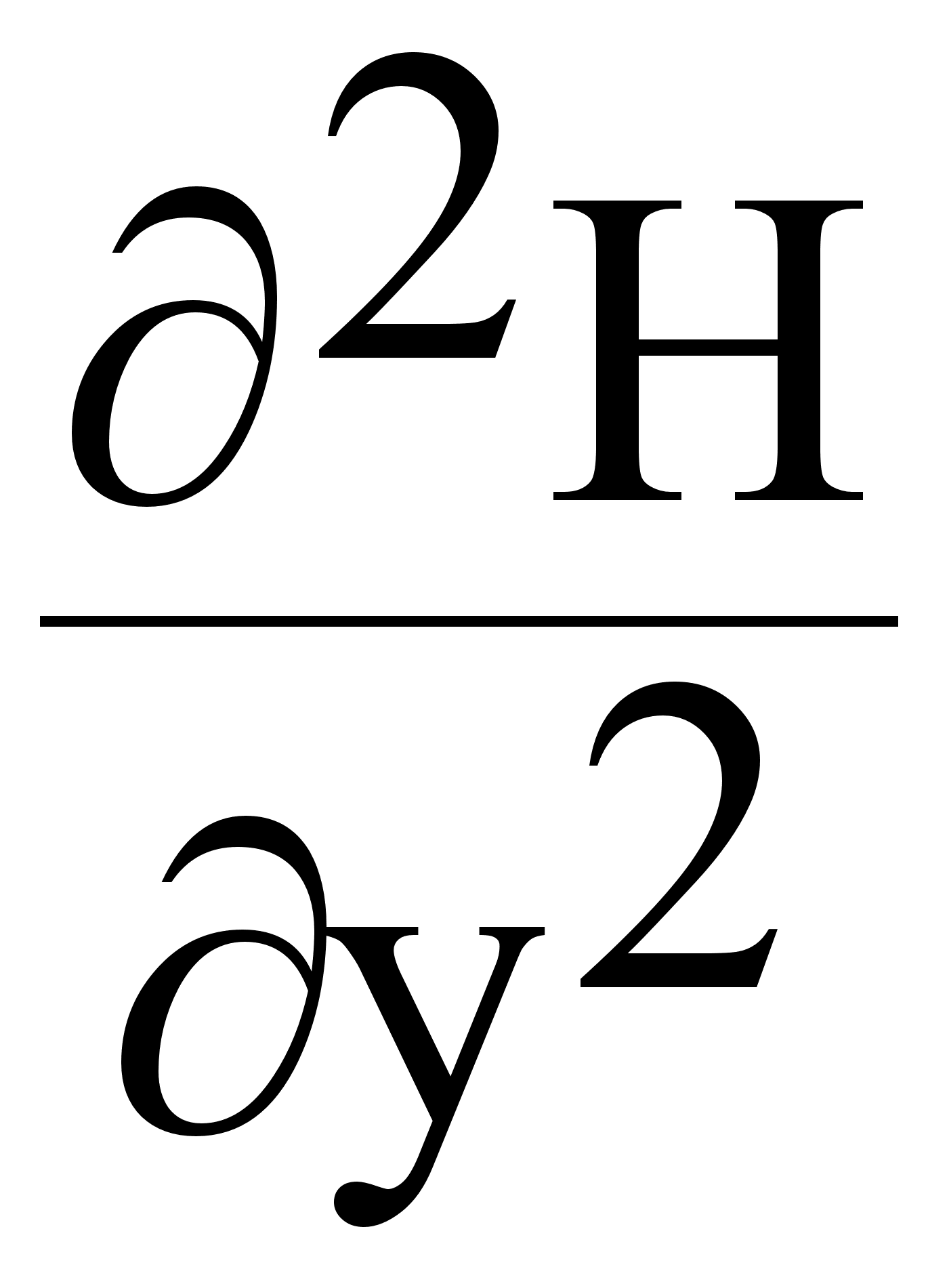
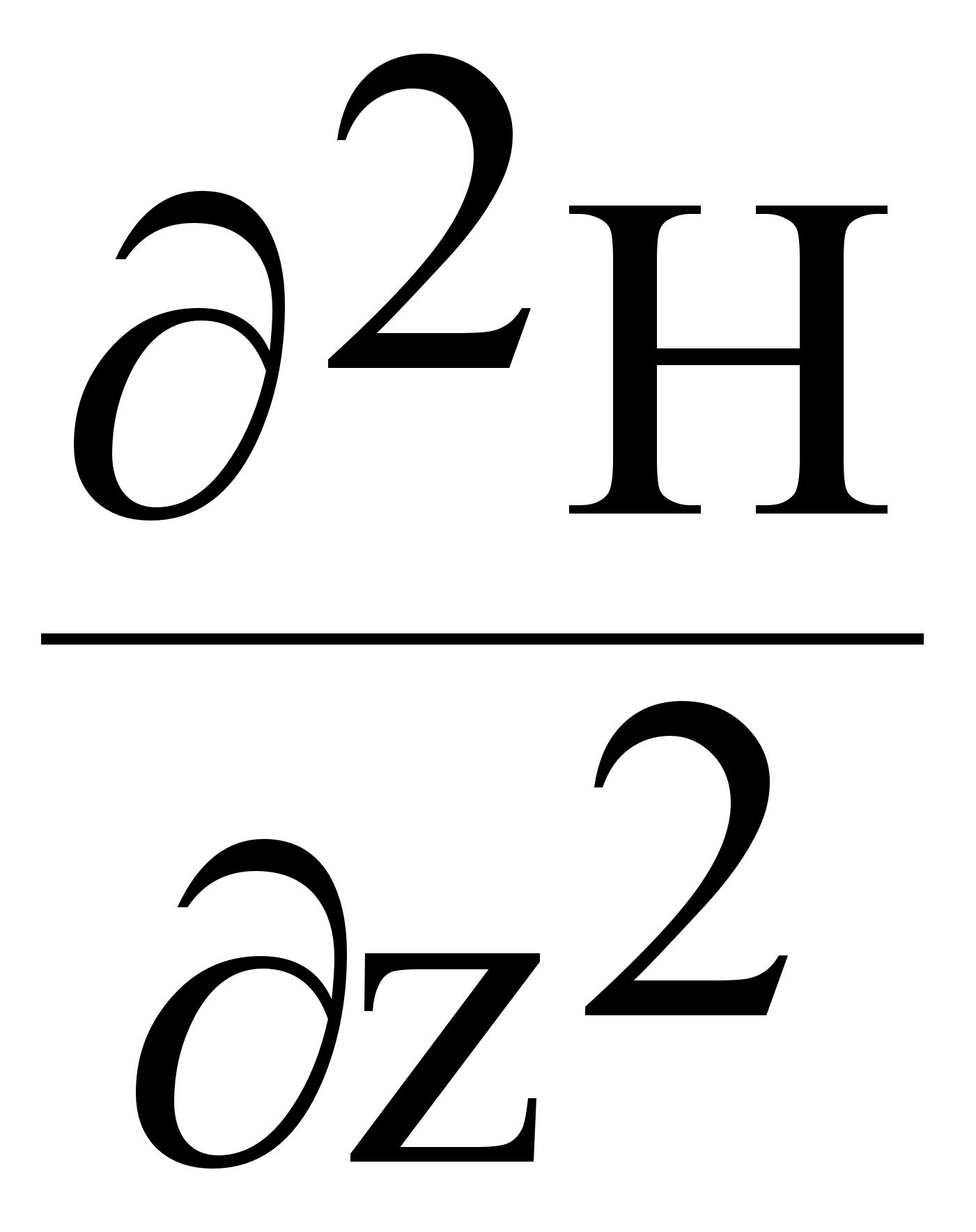
0 комментариев