Навигация
Лекция 7
Плоские электромагнитные
волны
7.1. Понятие волнового процесса.
7.2. Плоские волны в идеальной среде.
7.3. Плоские волны в реальных средах.
7.4.Распространение волнового пакета. Групповая скорость.
7.5. Поляризация ЭМВ.
7.1. Понятие волнового процесса.
Мир, в котором мы живем, - мир волн. Чем характеризуется мир волн, волновых процессов ?
Волновой процесс имеет следующие характерные признаки:
Волновой процесс всегда переносит энергию и импульсы. Нас интересуют волновые процессы ЭМВ.
Конечная скорость всех волновых процессов. В случае ЭМВ - это скорость света.
Независимость волновых процессов друг от друга. В этой комнате существуют поля самых разных частот, поля р/станций, света и т.д.
Волновые процессы, различные по физической природе, описываются одним и тем же математическим аппаратом.
Под волновым процессом понимают возмущение некоторой величины в пространстве, перемещающееся с конечной скоростью, переносящее мощность без переноса вещества.
7.2. Плоская ЭМВ в идеальной среде.
Под плоской ЭМ волной понимают волновой процесс, у которого составляющие электрического и магнитного полей изменяются в одинаковой фазе в плоскости перпендикулярной направлению распространения.
(7.2.1.) rot H = j a E Используем для анализа
1 - е и 2 - е уравнения
(7.2.2.) rot E = - j a H Максвелла
Источники, создающие плоские волны не входят в эти уравнения. Мы рассматриваем волновые процессы в дальней зоне, т.е. в пространстве за пределами
зарядов и токов. Решим уравнения относительно Е и Н.
Из уравнения (7.2.1.) выразим Е и подставим в (7.2.2.):
E
= (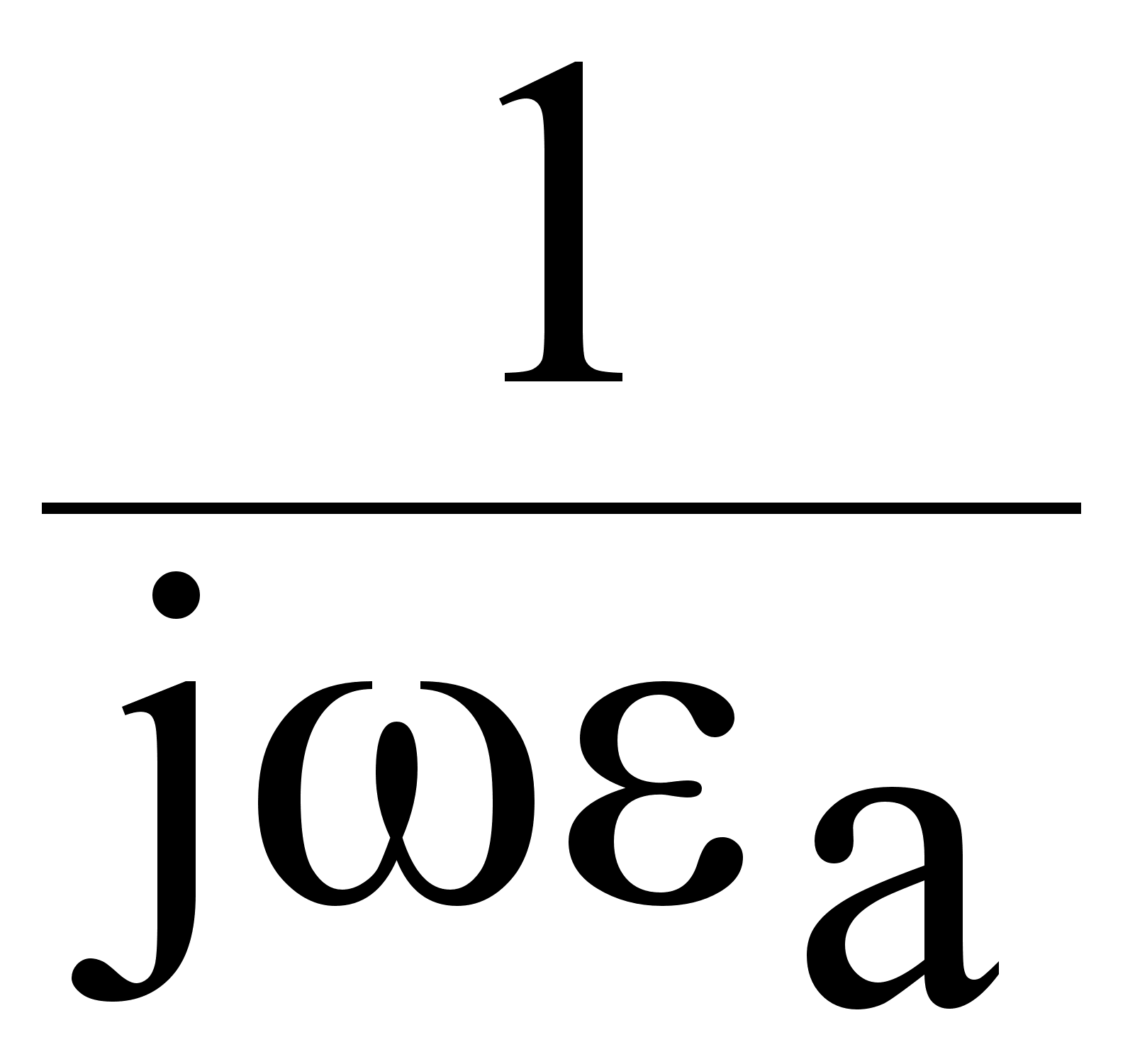 )
rot H
)
rot H
(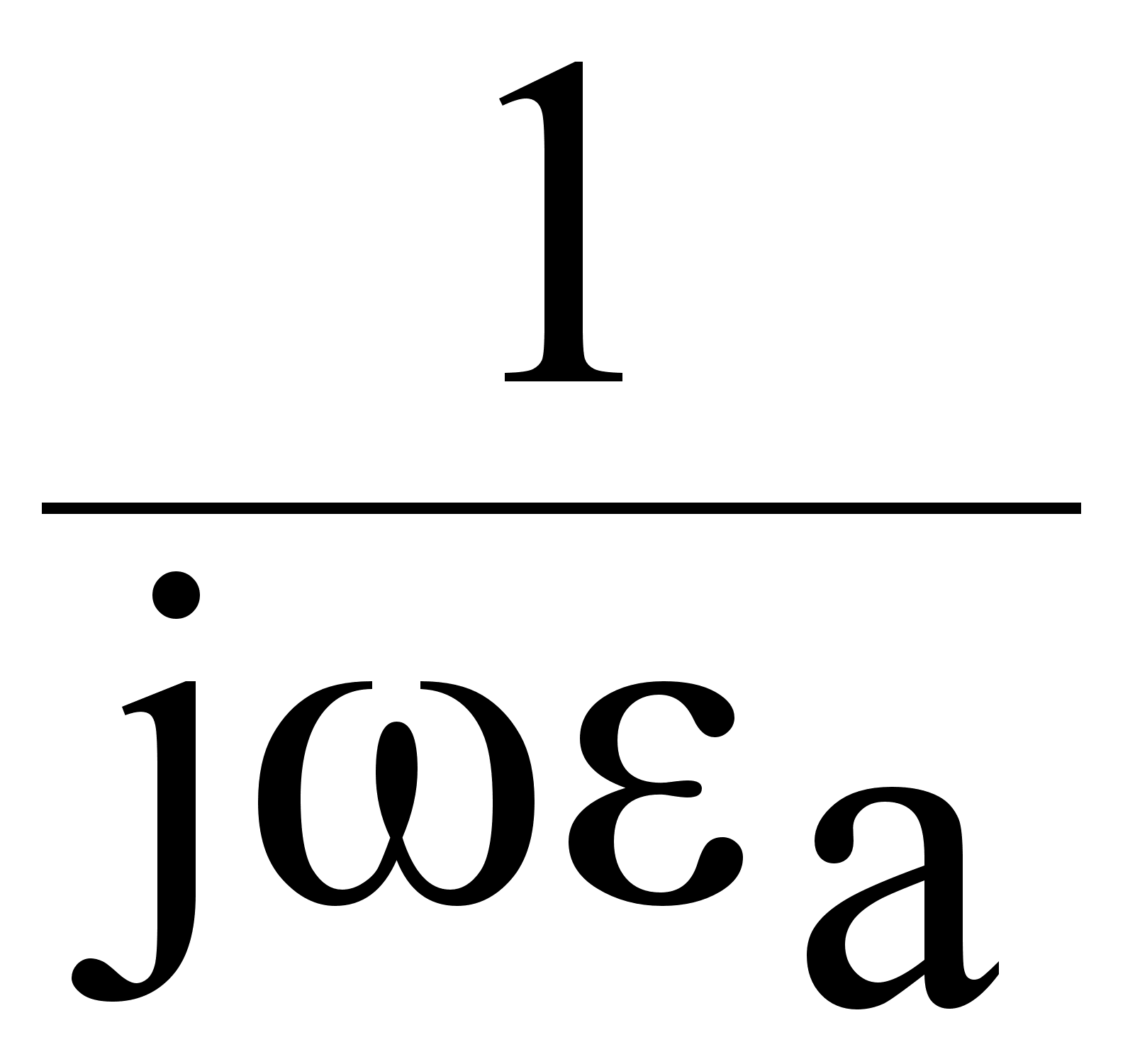 )
rot (rot H) = - ja
H
)
rot (rot H) = - ja
H
rot rot H = grad div A - 2 H
grad div H - 2 H = 2 aa H
т.к. div H = 0 - четвертое уравнение Максвелла
2 H + k2 H = 0 однородное волновое ур-е Гельмгольца (7.2.3.)
k2 = 2aa
Точно так же из второго уравнения получаем
уравнения для вектора Е:
2 E + k2 E = 0 - однородное волновое ур-е Гельмгольца (7.2.4.)
В развернутом виде запишем уравнения:
(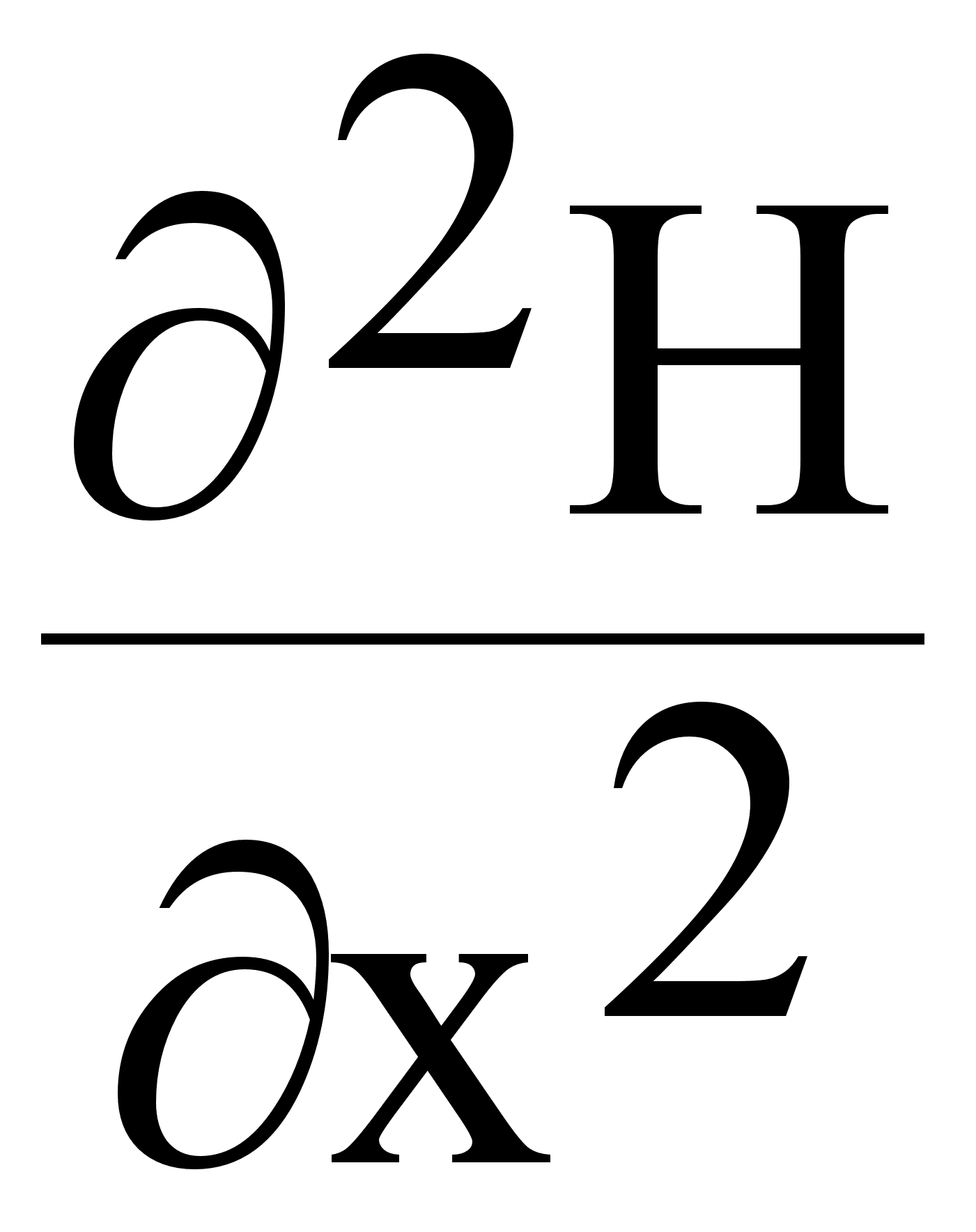 )
+(
)
+(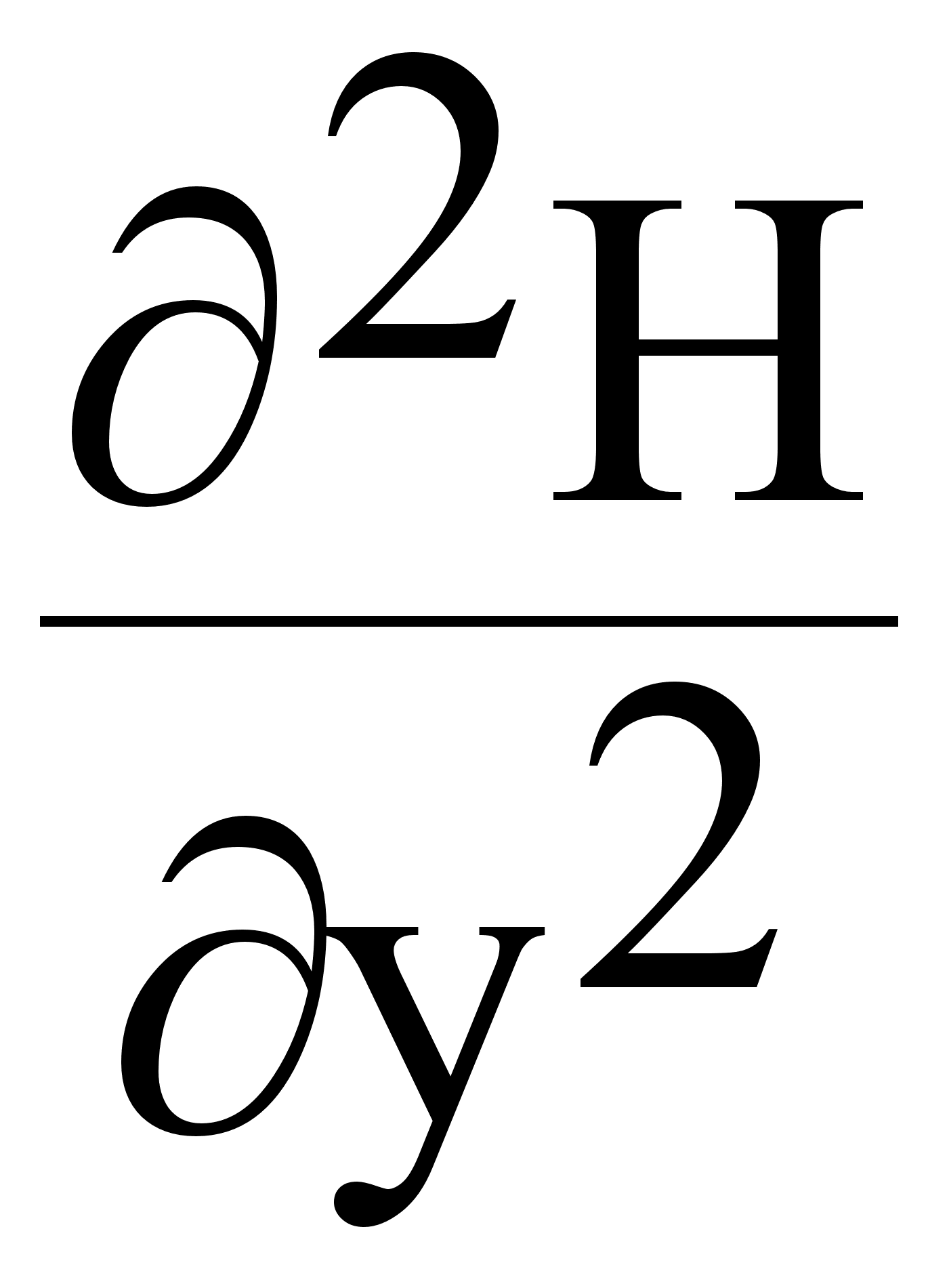 )
+(
)
+(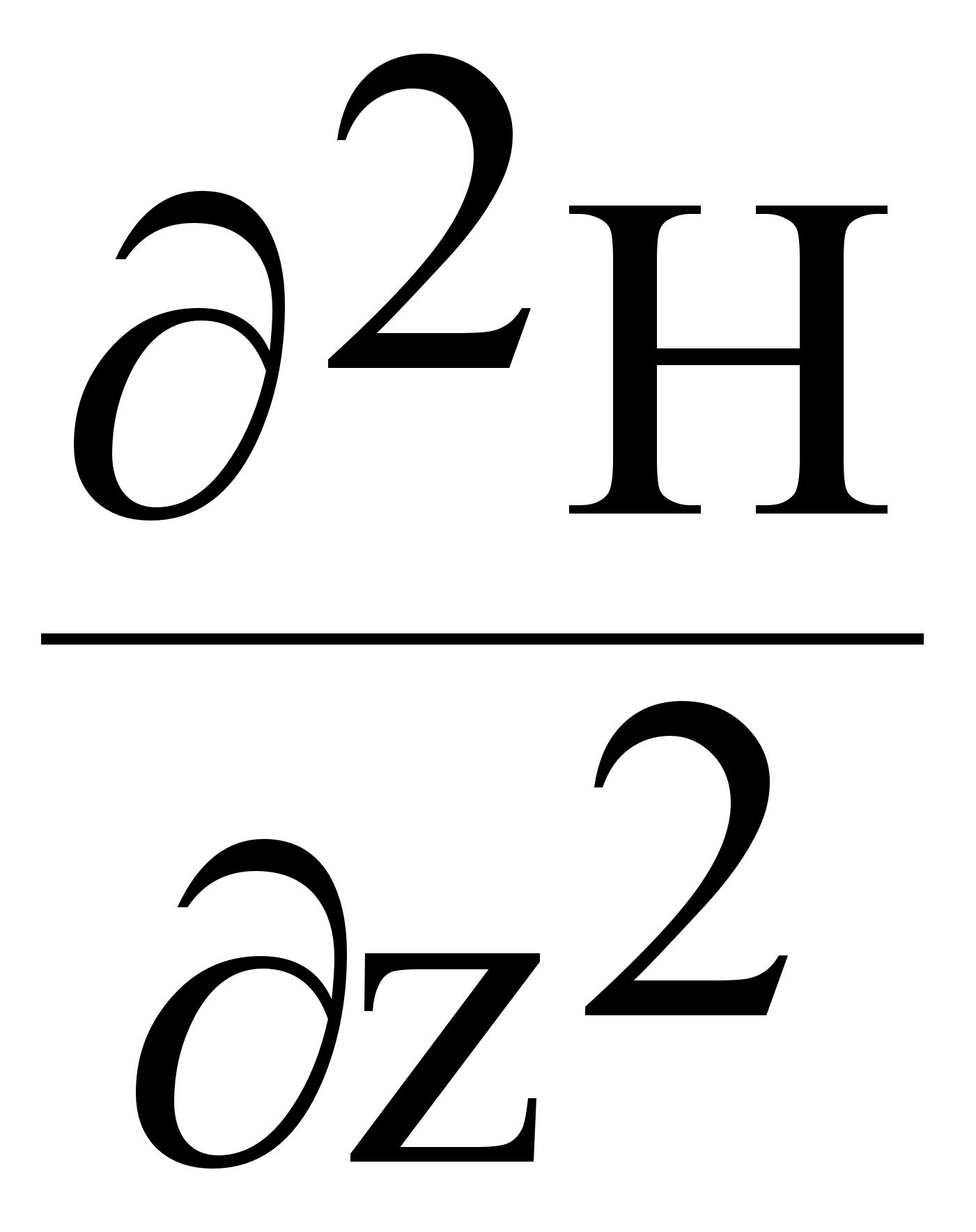 )
+ k2 H = 0 (7.2.5.)
)
+ k2 H = 0 (7.2.5.)
Решать такое уравнение трудно. Предположим, что источник ЭМ колебаний находится очень далеко от той области, где рассматриваем волны.

r1 r2 r3
т.к. источник очень далеко, то расстояния до точки можно считать одинаковым. Из физического смысла задачи, можно утверждать, что изменения полей по координате y, х нет, т.е.:
![]() =
=![]() = 0
= 0
(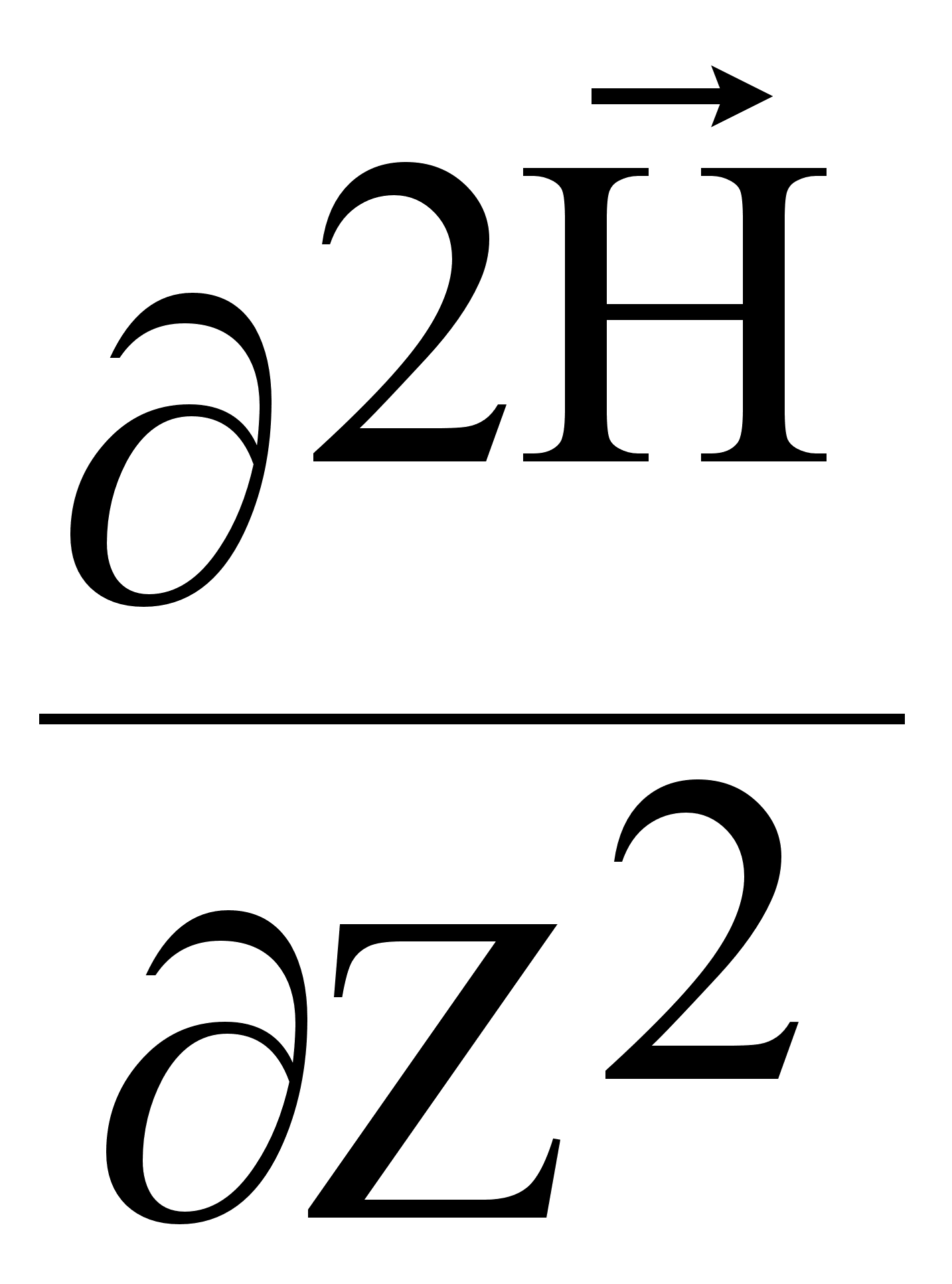 )
+ k2 H = 0 (7.2.6.)
)
+ k2 H = 0 (7.2.6.)
Для плоской ЭМВ волновое уравнение упрощается. Решение уравнения:
H(z) = A e - jkz + B e jkz в обычной форме
H(z,t) = ejt (A e - jkz + B e jkz) если поле зависит от времени.
H(z,t) = h означает, что поле векторное.
H(z,t) = h [A ej(t-kz) + B e j(t+kz)] (7.2.7.)
Выделим составляющую поля c амплитудой А:
Ha(z,t) = h A e j(t-kz) - в комплексной форме.
(7.2.8.)
Выделим из комплексного выражения действительную часть:
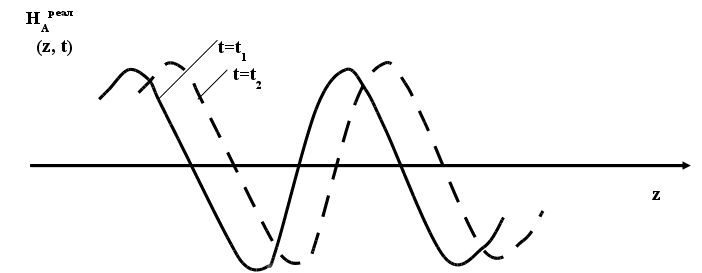
Haреал(z,t) = Re Ha(z,t) = h A cos(t - kz) (7.2.9.)
![]()
![]()
![]()
![]()
z1 z2
Фотография процесса в момент времени t = t1, t = t2. С какой скоростью перемещается фронт с одинаковой фазой ? Выясним это:
Ф1 = t1 - kz1 ; Ф2 = t2 - kz2 (7.2.10.)
Прибор регистрирует одинаковую напряженность, надо потребовать, чтобы Ф1 = Ф2
t1 - kz1 = t2 - kz2
k (z2 - z1) = (t2 - t1)
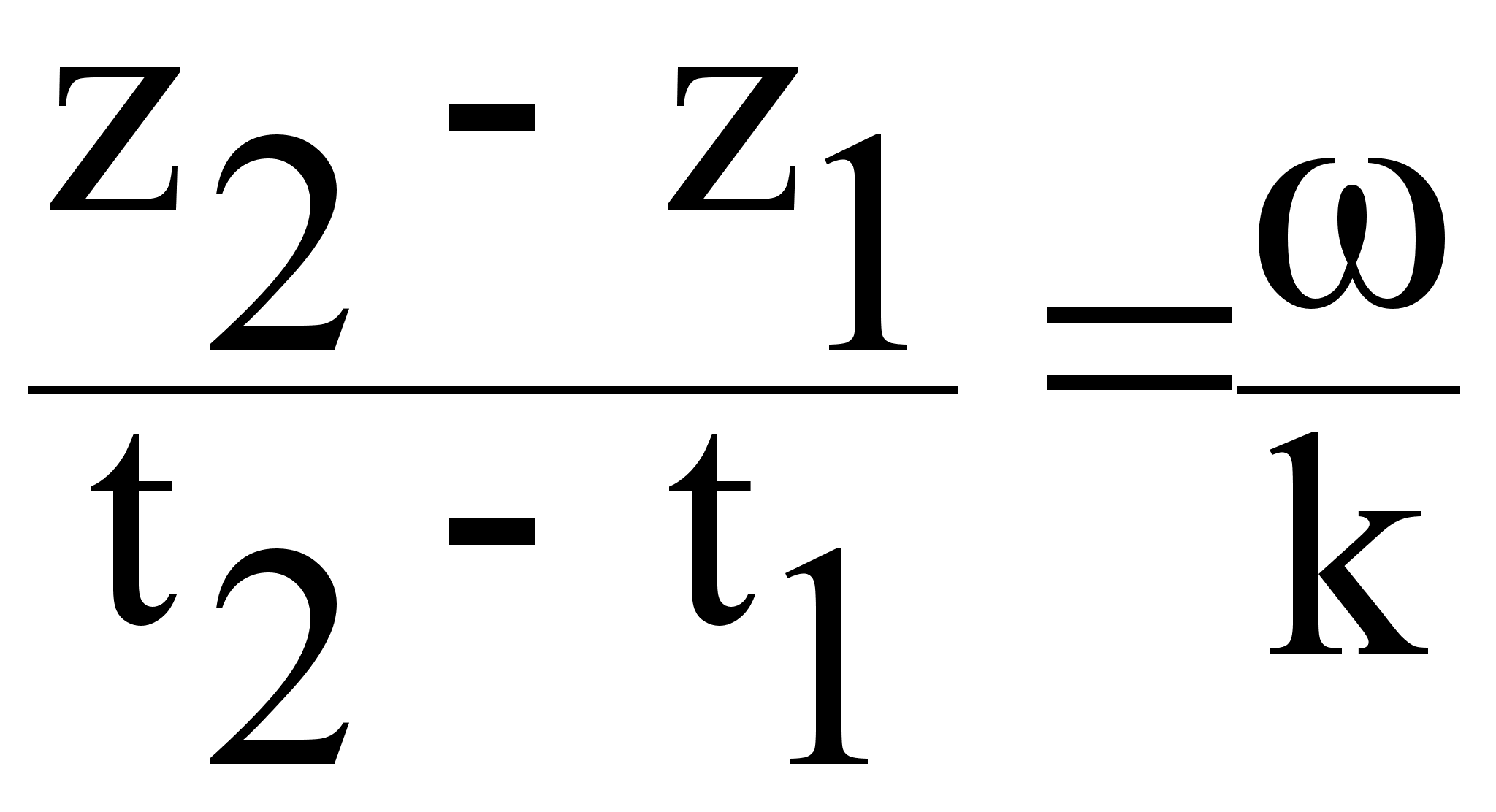 =
Vф -
называется
фазовой скоростью
волны.
=
Vф -
называется
фазовой скоростью
волны.
![]() k =
a
a
k =
a
a
Vф
= 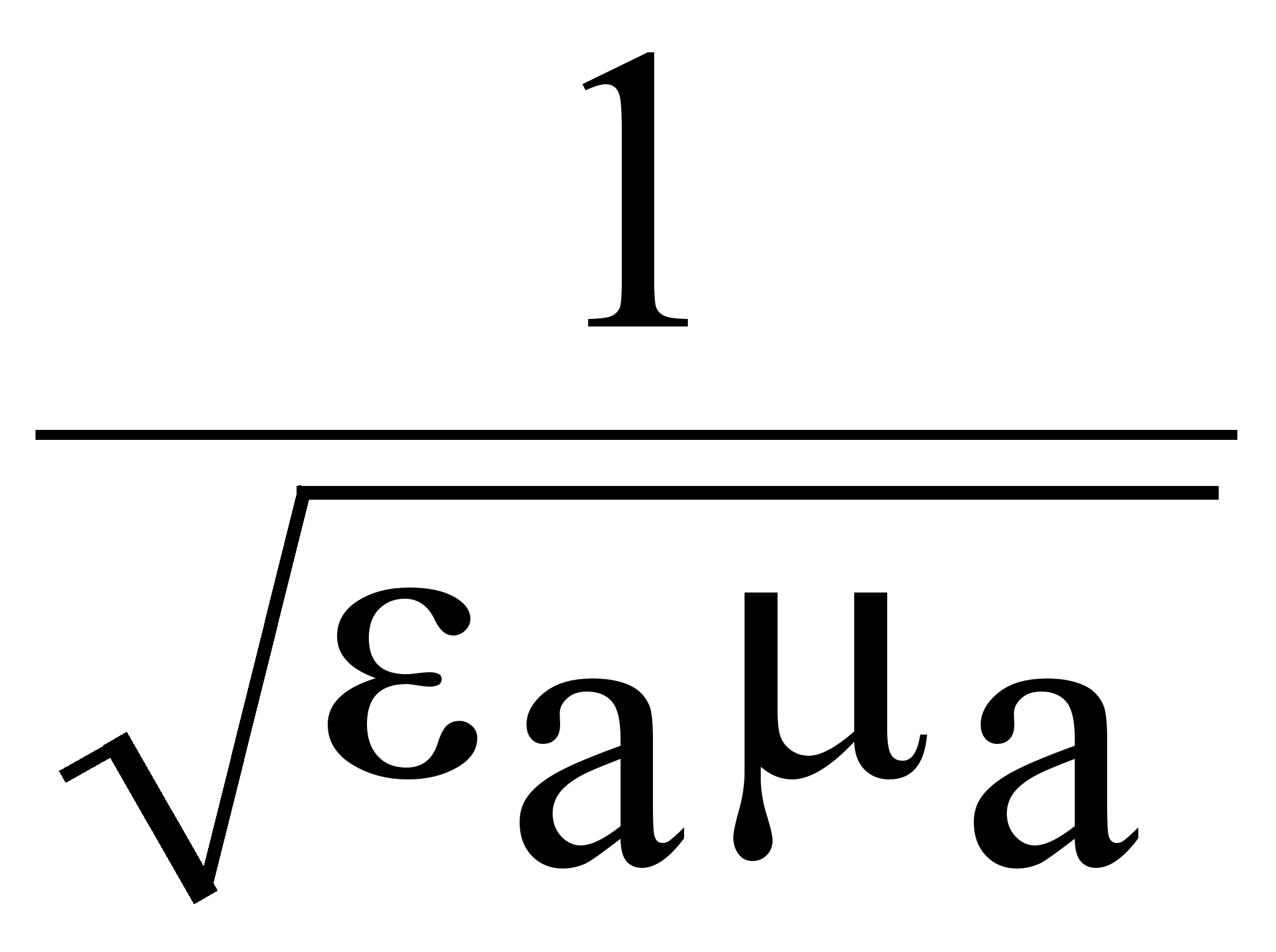 -
зависит от
свойств среды,
-
зависит от
свойств среды,
где распространяется ЭМВ.
0
= 8,85*10 –12![]() , 0
= 4*10-7
, 0
= 4*10-7![]() ,
,
V = 3*108![]() (7.2.11.)
(7.2.11.)
- называют пространственную периодичность волнового процесса.
- это длина пути, которую проходит фронт с одинаковой фазой за период, или- это есть расстояние, которое проходит фазовый фронт за 1 период.
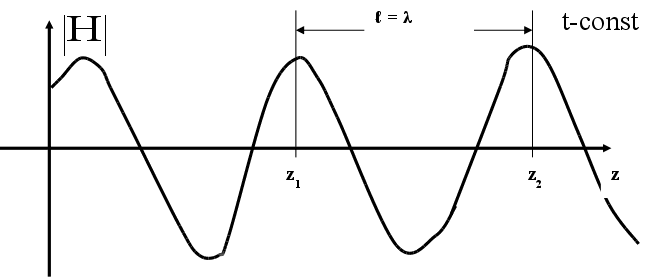
в т. Z1 Ф1 = t - kz1
в т. Z2 Ф2 = t - kz2
Ф1 - Ф2 = 2
z2
- z1 = ![]() =
=
k = ![]() - волновое
число
- волновое
число
Vф
= 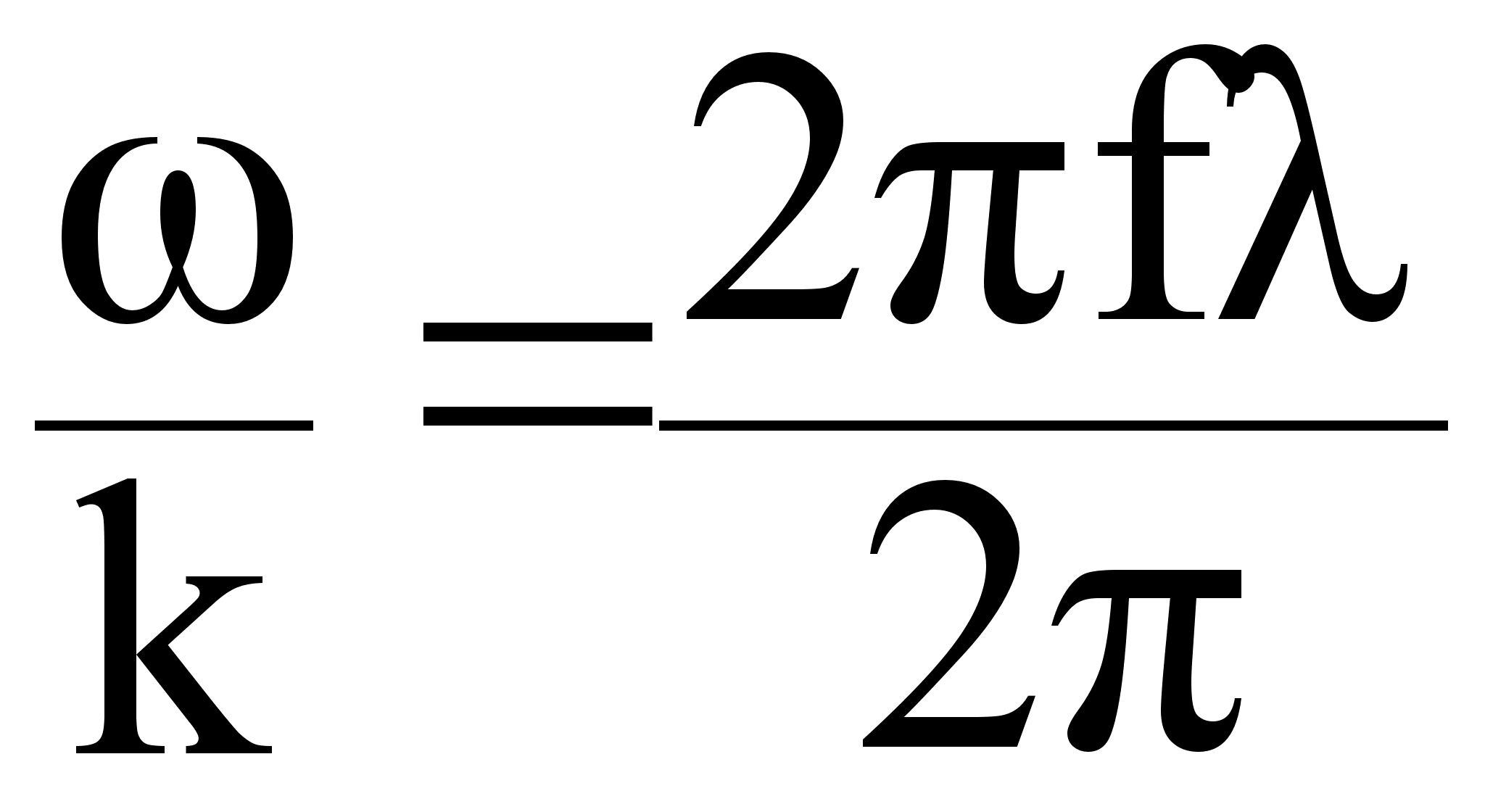 =
f если в вакууме,
то
=
f если в вакууме,
то
Vф = c
Vф = f (7.2.12.)
Выясним связь напряженностей Е и Н в ЭМВ:
rot H = j a E
rot E = - j a H
Спроектируем уравнение на оси координат:
![]()
![]() . . .
. . .
i j k
rot H =
![]()
![]()
![]()
Hx Hy Hz
-(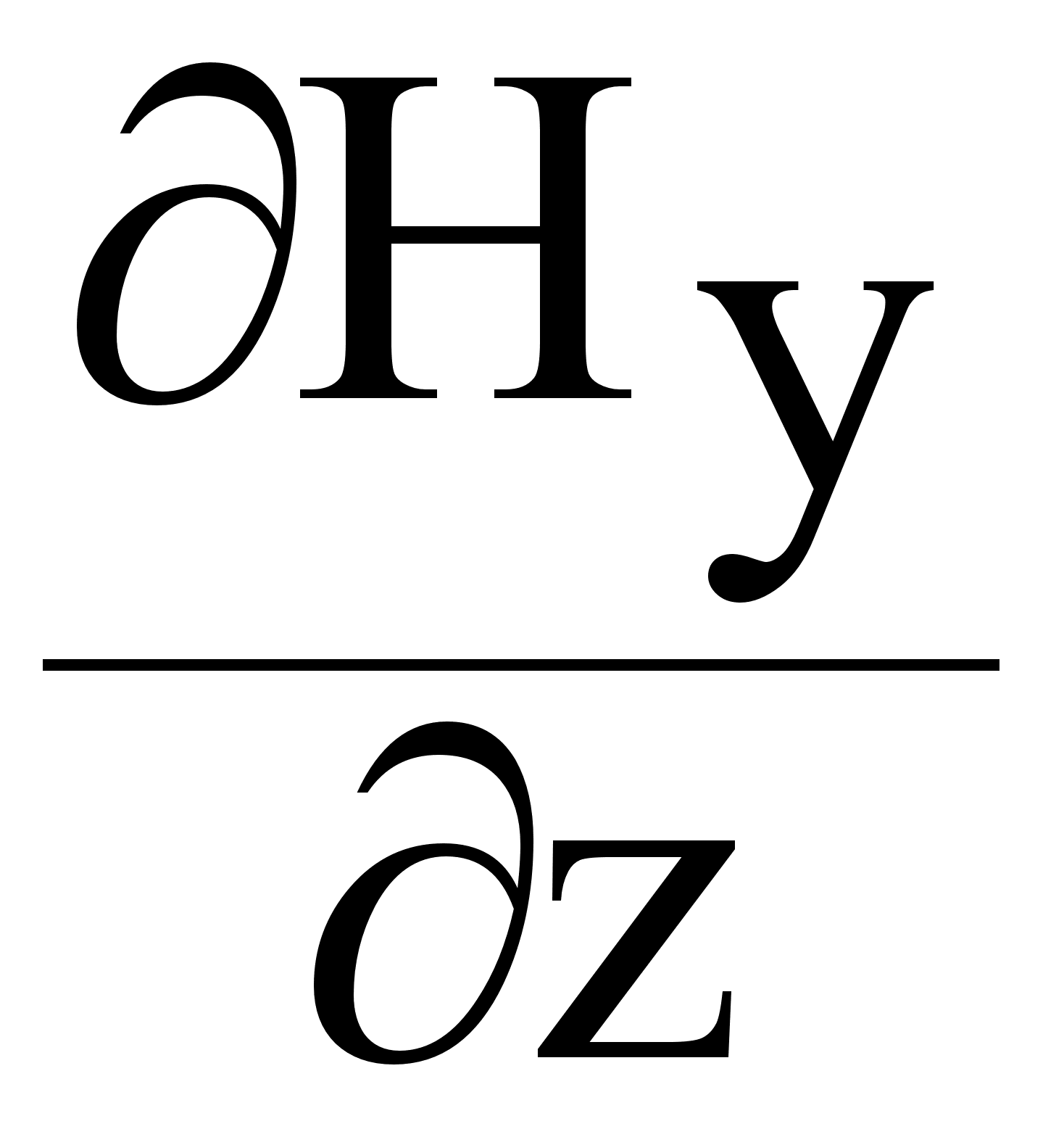 )
= ja
Ex
)
= ja
Ex
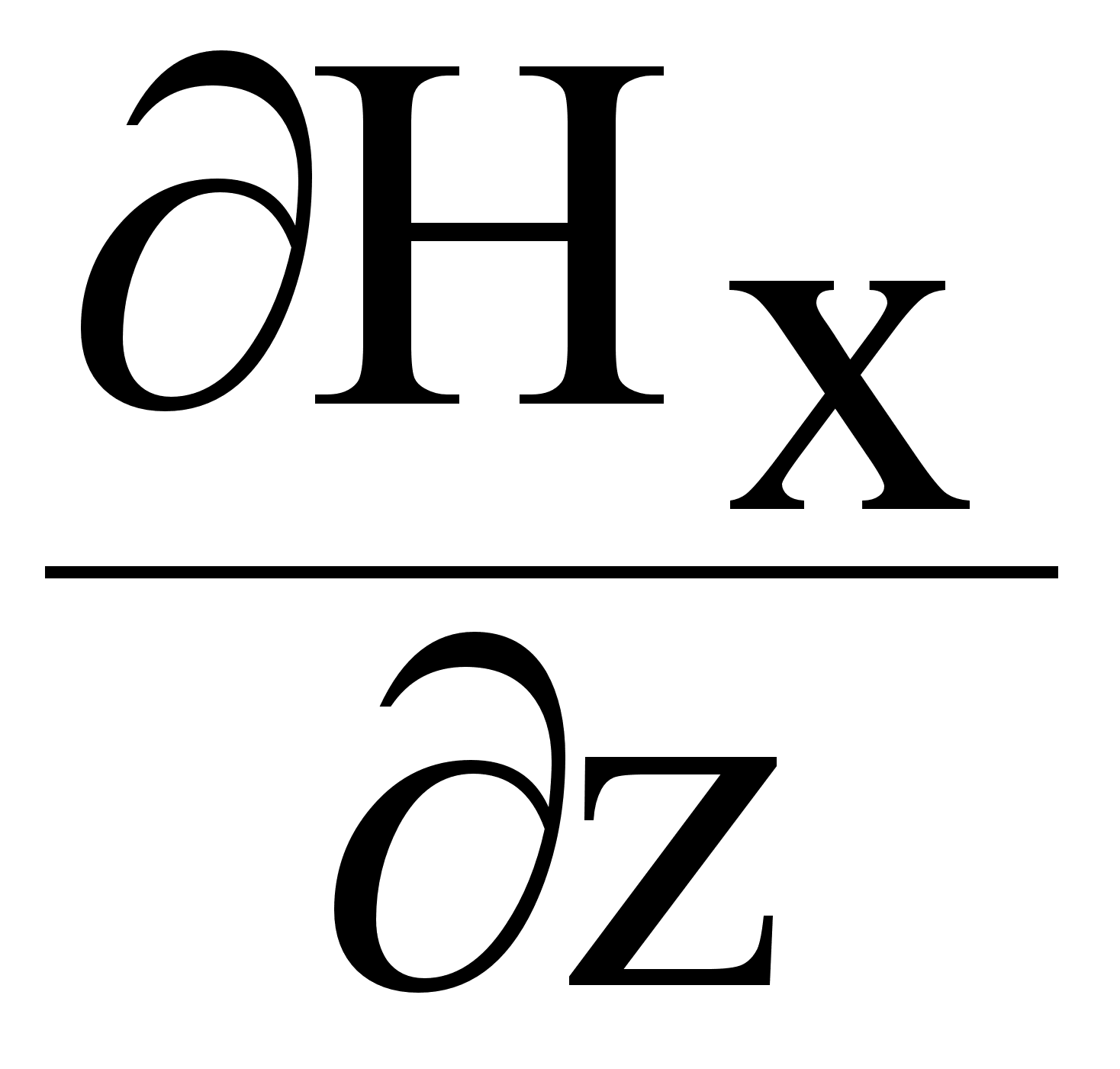 =
ja
E;
=
ja
E; 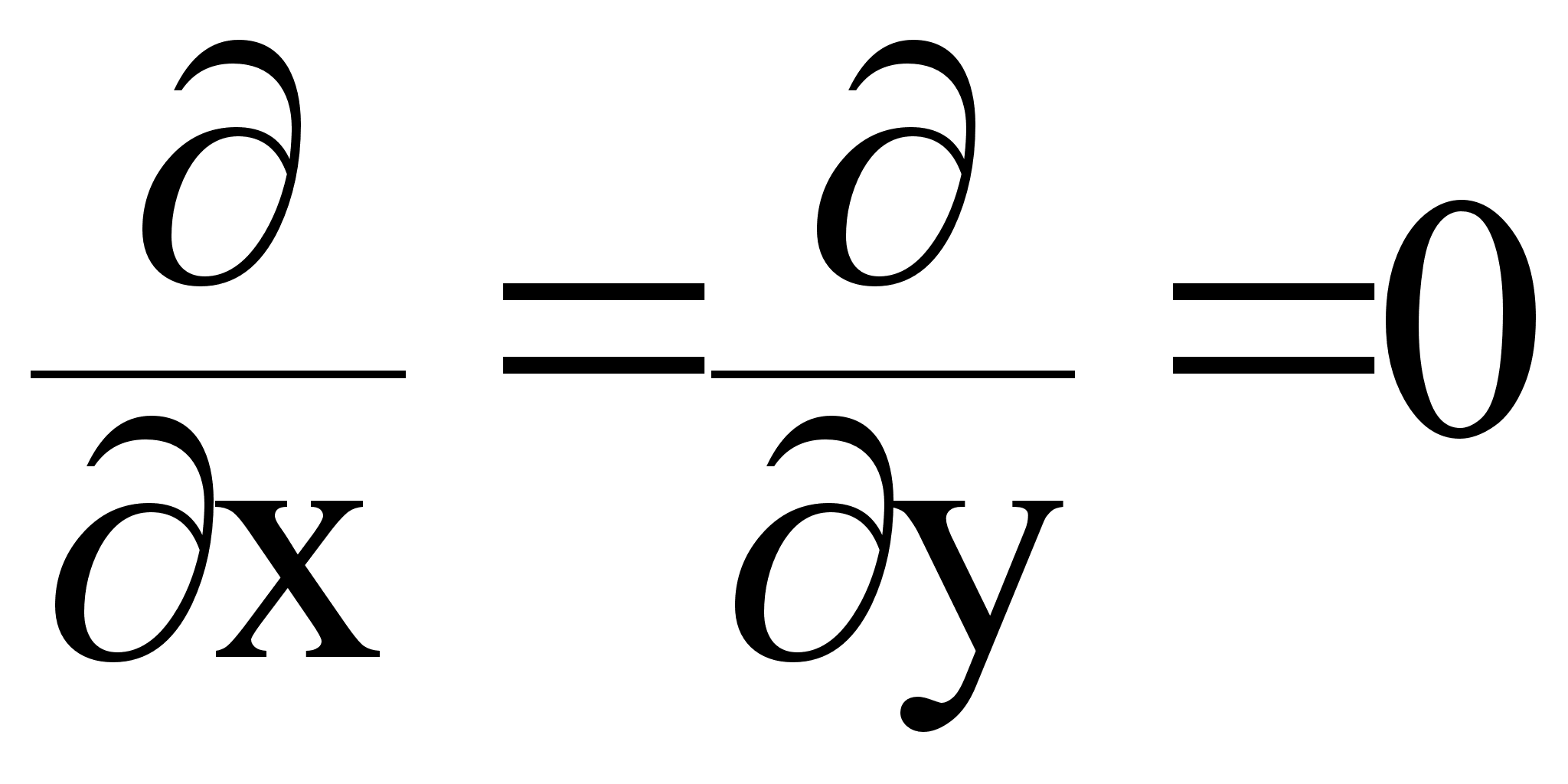
0 = ja Ez
Ez = 0
-(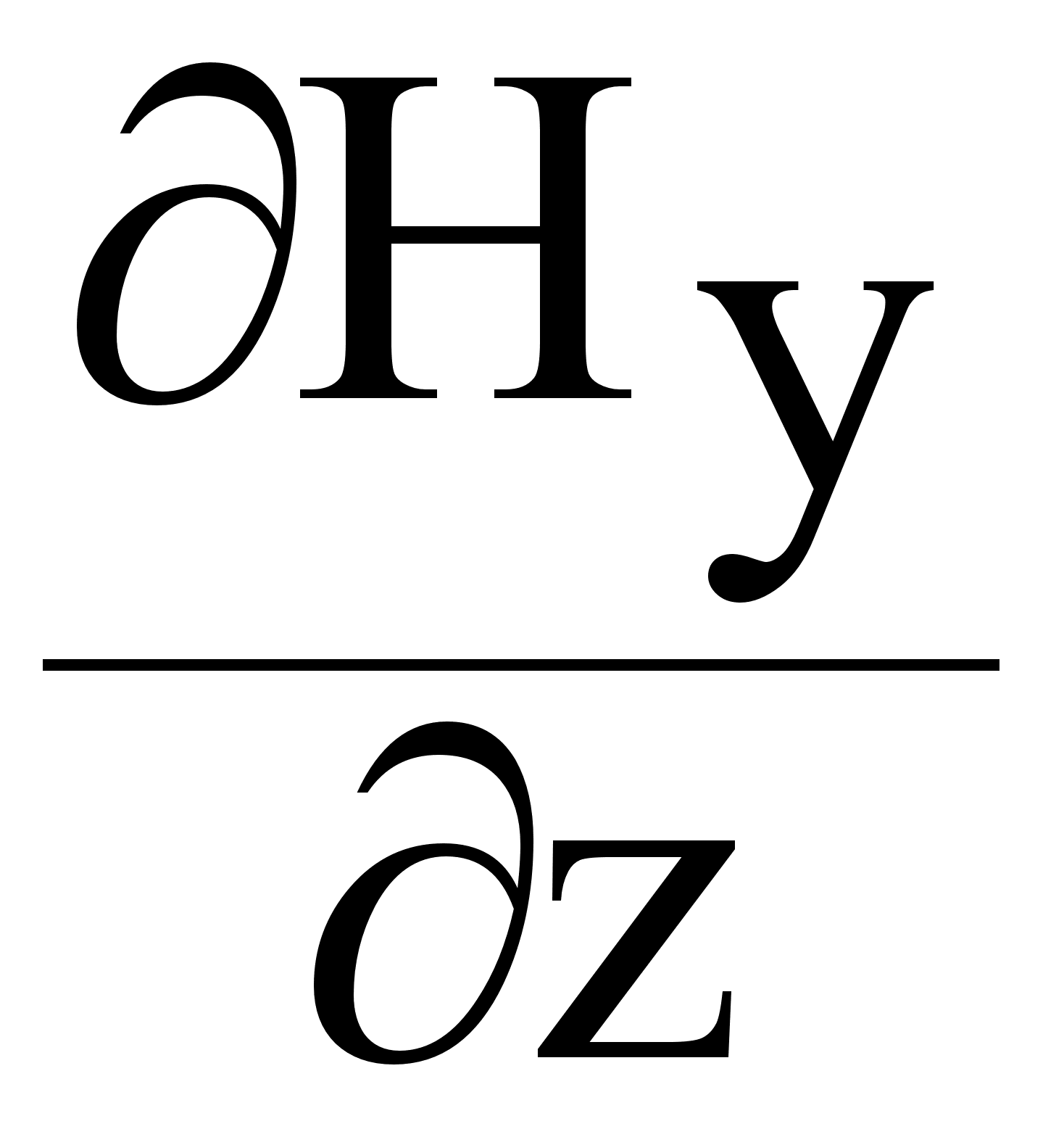 )
= - ja
Hx , 0 = -
jaHz
)
= - ja
Hx , 0 = -
jaHz
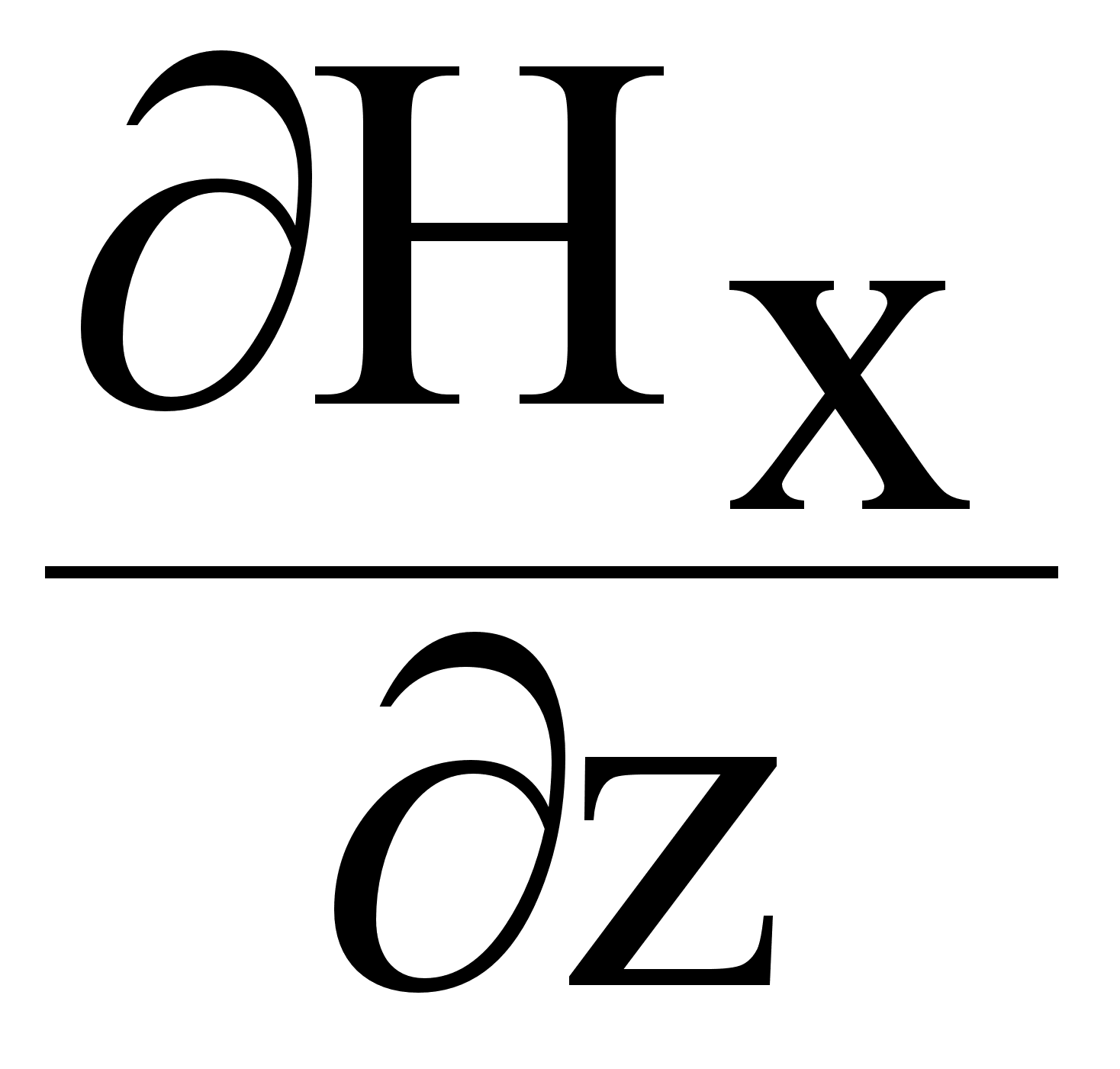 = - j a
Hy , Hz
= 0 (7.2.13.)
= - j a
Hy , Hz
= 0 (7.2.13.)
В ЭМВ отличны от нуля только две составляющие в плоскости плоскости распространения:
-(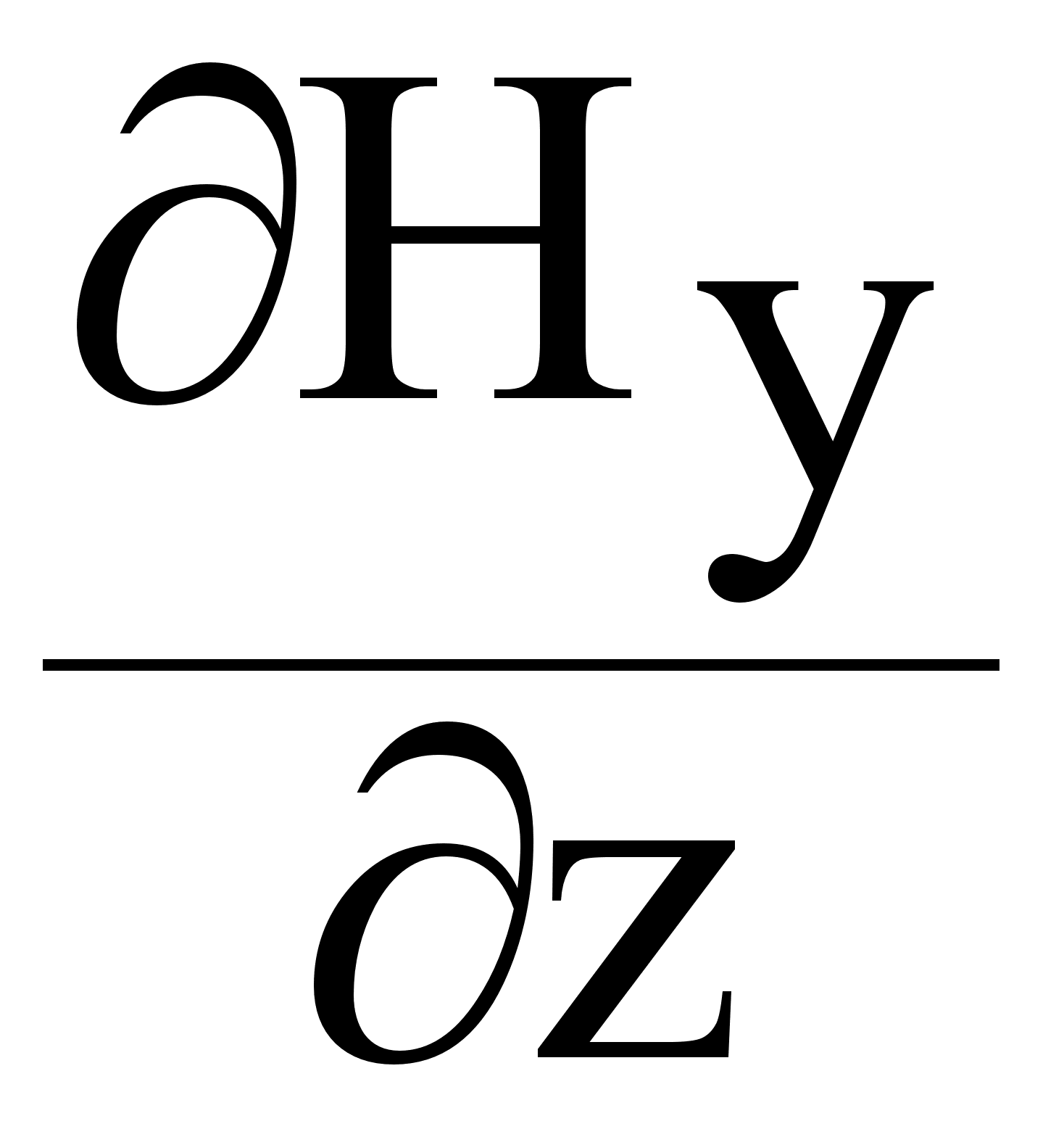 )
= jaEx
)
= jaEx
j k Hy = ja Ey
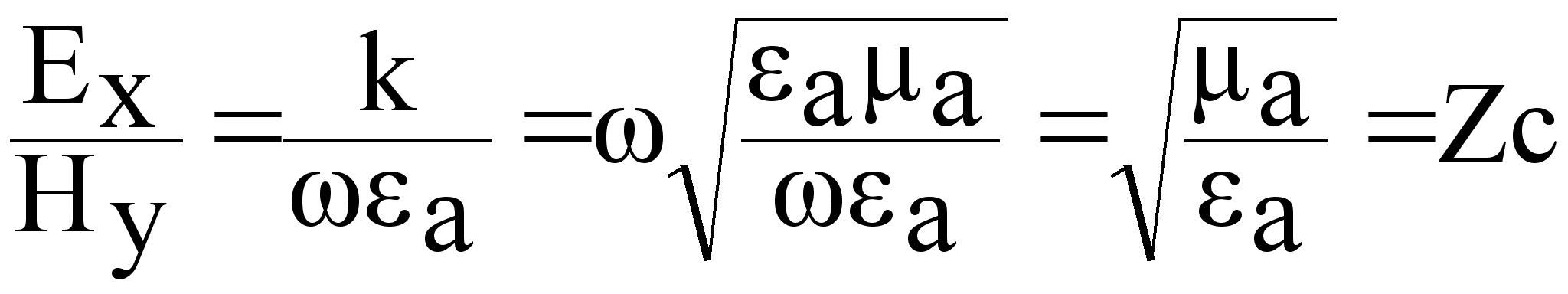 (7.2.14.)
(7.2.14.)
Это лишний раз подчеркивает, что сферические волны излучателя в дальней зоне превращаются в плоские ЭМВ.
Ориентация векторов Е и Н.
Для плоской ЭМВ Е всегда Н.
Покажем, что величина Е Н = 0:
E H = E H cos (E H) = 0
(i Ex + j Ey) (i Hx + j Hy)
ExHx + EyHy = Zc HyHx - ZcHxHy = 0
Ex = Zc Hy ; Ey = - Zc Hx
E H всегда в плоской ЭМВ
H = y0 A e j(t-kz) общая запись
плоской ЭМВ.
H = x0 A Zc e j(t-kz) (7.2.15.)
Поскольку в рассматриваемой задаче рассматривается только один источник, то учитываем только волну с амплитудой А. В пространстве имеются
2 взаимно перпендикулярных поля ( Е и Н). Как определить направление переноса энергии ?
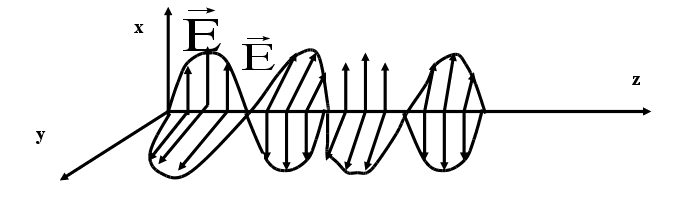

![]()
Пср
= (![]() )
Re [E H*]
)
Re [E H*]
Итоги:
Составляющие Е и Н лежат в плоскости перпендикулярной направлению распространения и изменяются в фазе (там где max Е там max Н, и наоборот)
Отношение ![]() = Zc определенная величина в случае вакуума Zc = 120 . Плоская ЭМВ однородная.
= Zc определенная величина в случае вакуума Zc = 120 . Плоская ЭМВ однородная.
Амплитуды Е и Н не зависят от поперечных координат.
У плоской ЭМВ Ez = 0 , Hz = 0.
Похожие работы
... в пространстве. Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна: где - скорость света в вакууме, , - электрическая и магнитная постоянные, , - соответственно диэлектрическая ...
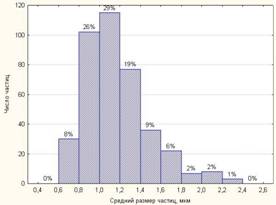
... поле – 2. Исследованиями установлено, что воздействие ультразвуковых колебаний на исходный порошок через жидкую среду приводит к его некоторому измельчению за счет разрушения агломератов. Сравнение микроструктуры керамики ЦТБС-3М, полученной различными методами, позволяет сделать вывод, что наименьшая пористость наблюдается у образцов, синтезированных из пресс-заготовок, полученных из порошка, ...
... переменного тока проводимости или тока смещения, где длина волны зависит от частоты колебания. Любой электрический ток, согласно электродинамике, всегда замкнут. Поэтому продольные электромагнитные волны всегда замкнуты независимо от того, представляют они переменный электрический ток проводимости или смещения. Продольные электрические возмущения поля имеют продольную ориентацию электрического ...
... потока Ф0 ...» Физические величины (справочник). 1991. С.1234. «Собственно говоря, постоянной Планка называется коэффициент пропорциональности ...» Квантовая физика. И.Е.Иродов. 2001. С.11. Электромагнитная волна де Бройля, как и фотон, представляет электромагнитный квант, состоящий из кванта электрического потока (заряда) и кванта магнитного потока. Длина волны де Бройля и энергия ...
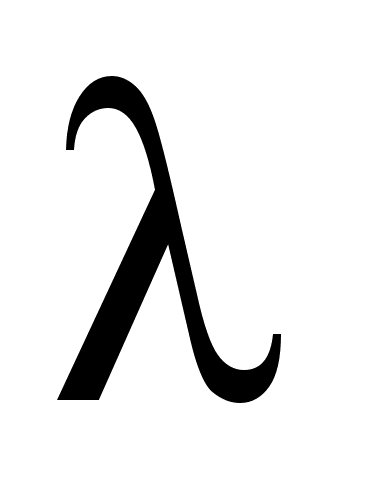
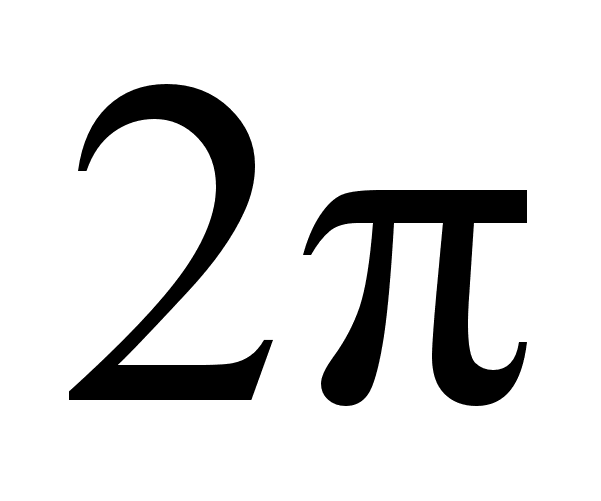
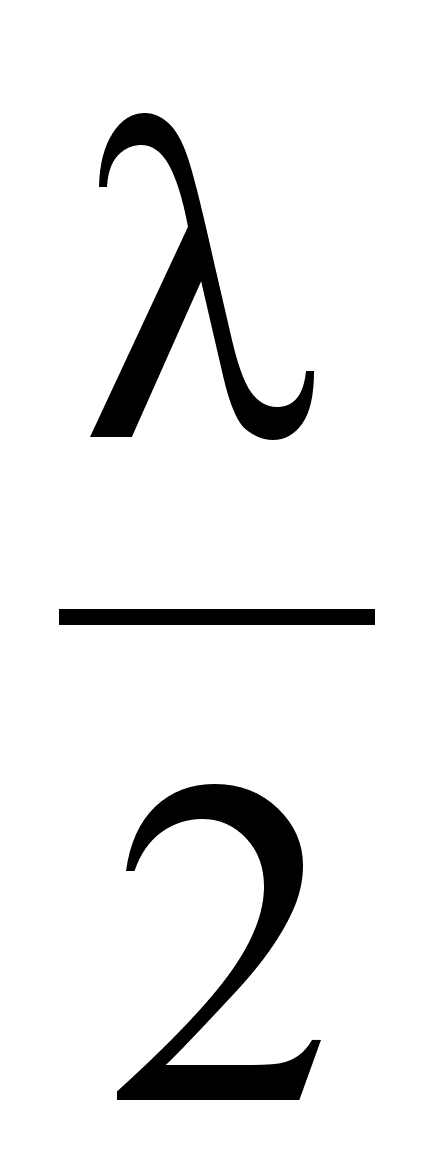
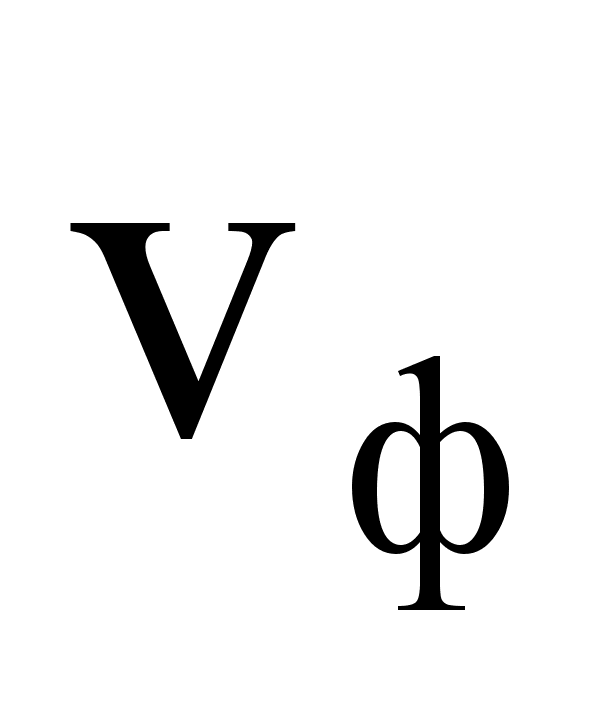


0 комментариев