Навигация
Побудова економетричної багатофакторної моделі виконання місцевих бюджетів
2.3 Побудова економетричної багатофакторної моделі виконання місцевих бюджетів
Лінійна багатовимірна модель (ЛБМ) має такий вигляд
y=β0+ β1x1+ … + βpxp (2.1)
y – Залежна змінна – ендогенна змінна
x1, x2…xp – залежні змінні – екзогенні змінні.
Отже для побудови економетричної багатофакторної моделі залежності місцевого бюджету вибираємо наступні змінні:
Y – надходження до бюджету;
X1 – державне управління;
X2 – соціальний захист та соціальне забезпечення;
X3 – цільові фонди органів місцевого самоврядування;
X4 – кошти, що передаються до бюджету розвитку;
X5 – послуги, що пов’язані з економічною діяльністю.
Саме за допомогою цих змінних проведемо регресійний та дисперсійний аналіз, знайдемо залежність надходжень від видатків місцевого бюджету, а також побудуємо модель цієї залежності.
Таблиця 2.5
Дані для регресійного аналізу:
| Y | X1 | X2 | X3 | X4 | X5 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 3993939 | 32675,6 | 17220726 | 43,2 | 20612,7 | 545,6 |
| 685033 | 49881,8 | 229078,2 | 297,4 | 35575 | 1457,8 |
| 983166 | 81018,6 | 342880,3 | 448 | 59668,4 | 6702,4 |
| 409041 | 41431,8 | 163010,8 | 144,4 | 25451,4 | 32764,8 |
| 638359 | 64637,5 | 241734 | 197,4 | 54333,1 | 64396 |
| 895032 | 95719,2 | 369295,2 | 282,8 | 79328,5 | 79770 |
| 517764 | 54403,8 | 173552,1 | 233,4 | 9683,7 | 600718 |
| 814398 | 82290,5 | 260067,9 | 373 | 26264 | 14962,7 |
| 1159824 | 122184 | 396080,3 | 24896,1 | 56407,1 | 25307 |
У зв’язку з тим, що економетрична модель обов’язково має випадкову помилку, модель (2.3.1) переписується у вигляді (2.3.2)
y=β0+ β1x1+ … + βpxp+ε (2.2)
де ε – випадкова помилка або перешкода.
Регресійні коефіцієнти визначають за допомогою методів найменших квадратів.
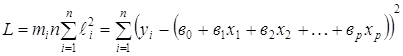 (2.3)
(2.3)
Візьмемо частичні похідні по кожному з виразів, дорівняти їх і отримаємо систему рівнянь
![]() (2.4)
(2.4)
Ця система рівнянь має спеціальну назву – нормальна система.
Отримаємо цю систему:
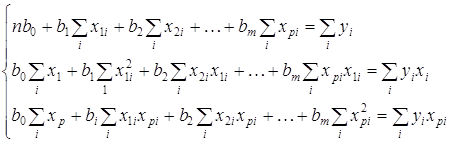 (2.5)
(2.5)
Невідомі у системі (2.3.5) – це коефіцієнти в0, в1...
х1, y1 – ми маємо внаслідок спостережень
в0, в1 - це коефіцієнти, які ми повинні визначити
n – кількість спостережень, вони нам завжди відомі.
Якщо центрувати наші дані, необхідно замість х1 записувати:
![]() (2.6)
(2.6)
По діагоналі системи будемо мати дисперсію відпов. змінною, а недіагональні елементи нормальної системи будуть коваріаціями відповідних пар елементів.
Перевірку якості отриманого рівняння ми починаємо з побудови таблиці дисперсійного аналізу регресійного рівняння.
Таблиця 2.6
Дисперсійний аналіз регресійного рівняння
| Джерело варіації | SS | df | MSS |
| Регресія | 9,67E+12 | 5 | 1,93E+12 |
| Залишки | 4,36E+10 | 3 | 1,45E+10 |
| Загальне | 9,71E+12 | 8 |
ŷ – обчислене значення
y – фактичне значення
![]() - середнє значення (фактичне)
- середнє значення (фактичне)
n – кількість спостережень
p – кількість коефіцієнтів, які ми визначаємо
Якщо величина F буде більше Fтабл, то ми вважаємо, що наше рівняння значуще.
Вираз поділимо зліва та справа на величину SST, тоді отримаємо
![]() (2.7)
(2.7)
Величина ![]() отримала спеціальне позначення:
отримала спеціальне позначення:
R2 спеціальну назву – коефіцієнт детермінації
![]() = R2 (2.8)
= R2 (2.8)
R2=1-![]() (2.9)
(2.9)
Фізичний зміст цієї величини: вона показує, яку долю загальної дисперсії пояснює наше рівняння регресії, в даному випадку R2 = 0,995515.
Коефіцієнт детермінації використ.для порівняння якості конкуруючих регресійних моделей, кожна з якої значуща.
Те рівняння буде краще, для якого коефіцієнт детермінації буде більше.
Для того, щоб порівняти якість конкуруючих регресійних моделей, треба, щоб у них співпали кількість спостережень та змінних.
Можна довести, що величина
SST = SSR + SSE
8 = 5 + 3
У загальному випадку для порівняння моделей використовують скоригований коефіцієнт детермінації:
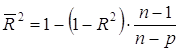 (2.10)
(2.10)
Для перевірки стат-го зв’язку між вибраними змінними та величиною y використовують коефіцієнт множинної кореляції: R- позначення цього коефіцієнта.
Можна показати, що коефіцієнт детермінації рівняється квадрату коефіцієнта кореляції.
Властивості коефіцієнта множинної кореляції R та парного коефіцієнта кореляції r :
Таблиця 2.7
Властивості коефіцієнта множинної кореляції R та парного коефіцієнта кореляції r
|
| rxy |
| 0<R<1 |
|
| 0,995515 | 0,995515=0,995515 |
Чим більше по модулю величина R і r, тим зв’язок тісніший між величиною y і xp.
Чим більше по модулю величина R і r, тим зв’язок тісніший між величиною y і xp.
Так як r<0, то збільшенню однієї з величин відповідає зменшення іншої.
Коефіцієнт множинної кореляції = 0,99775.
Для перевірки значущості отриманих коефіцієнтів (якщо в цілому за критерієм f рівняння було значущим) використовуємо критерій ст’юдента.
Для перевірки значущості кожного коефіцієнта регресії обчислюють величину
![]() (2.11)
(2.11)
bi – обчислене значення коефіцієнта
![]() - це його середньоквадратичне відхилення.
- це його середньоквадратичне відхилення.
Чим величина ![]() більше, тим більш значущим є отриманий коефіцієнт.
більше, тим більш значущим є отриманий коефіцієнт.
Величину ![]() порівнюють з величиною tтабл .
порівнюють з величиною tтабл .
Якщо ![]() > tтабл , то вважаємо, що рівняння значуще.
> tтабл , то вважаємо, що рівняння значуще.
У свою чергу tтабл розподілено згідно з розподілом ст’юдента з n-p степенями свободи на рівні значущості α.
α – імовірність помилки.
Якщо α=0,01, то ми можемо помилитись 1 раз із 100.
Якщо прийняти α=0,05, то , якщо p-value<0,05, то коефіцієнти значущі.
Визначення коефіцієнтів регресії у стандартизованій формі.
Для того, щоб отримати рівняння у стандартизованих змінних, перетворюють і величину y і змінні х таким чином:
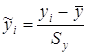 (2.12)
(2.12)
~ - символ стандартизації
Кожну змінну х перетворюємо аналогічно:
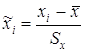 (2.13)
(2.13)
Отже лінійна багатовимірна модель матиме вигляд:
Y = 149794 + 7,862769 + 0,208411 + 0,96028 + 0,05365 + 0,1896
Розв’язавши відносно величини в всю систему , отримаємо коефіцієнти регресії у стандартизованій формі.
Таблиця 2.8
Вихідні дані по задачі
| y | x1 | x2 | x3 | x4 | x5 |
| 3993939 | 0,81813 | 431,171 | 0,00108 | 0,5161 | 0,01366 |
| 685033 | 7,28167 | 33,4405 | 0,04341 | 5,19318 | 0,21281 |
| 983166 | 8,24058 | 34,8751 | 0,04557 | 6,069 | 0,68172 |
| 409041 | 10,129 | 39,8519 | 0,0353 | 6,22221 | 8,01015 |
| 638359 | 10,1256 | 37,868 | 0,03092 | 8,51137 | 10,0877 |
| 895032 | 10,6945 | 41,2606 | 0,0316 | 8,86321 | 8,91254 |
| 517764 | 10,5075 | 33,5195 | 0,04508 | 1,87029 | 116,022 |
| 814398 | 10,1045 | 31,9338 | 0,0458 | 3,22496 | 1,83727 |
| 1159824 | 10,5347 | 34,15 | 2,14654 | 4,86342 | 2,18197 |
Таблиця 2.9
Вивід результатів
| Множинний R | 0,997755 |
| R-квадрат | 0,995515 |
| Нормований R-квадрат | 0,988039 |
| Стандартна помилка | 120507 |
| Спостереження | 9 |
Таблиця 2.10
Дисперсійний аналіз
| df | SS | MSS | F | Значимість F | |
| Регресія | 5 | 9,67E+12 | 1,93E+12 | 133,1719 | 0,001016 |
| Залишок | 3 | 4,36E+10 | 1,45E+10 | ||
| Всього | 8 | 9,71E+12 |
Таблиця 2.11
Дисперсійний аналіз
| Коефіцієнти | Стандартна помилка | t-статистика | P-Значення | Нижні 95% | Верхні 95,0% | |
| Y пересечение | 149794 | 184885 | 0,810201 | 0,477128 | -438592 | 738180,5 |
| Змінна X 1 | 7,862769 | 3,538394 | 2,22213 | 0,112819 | -3,39798 | 19,12352 |
| Змінна X 2 | 0,208411 | 0,009435 | 22,08948 | 0,000203 | 0,178385 | 0,238437 |
| Змінна X 3 | 0,96028 | 8,672742 | 0,11072 | 0,918828 | -28,5608 | 26,64026 |
| Змінна X 4 | 0,05365 | 3,291805 | -0,0163 | 0,98802 | -10,5296 | 10,42235 |
| Змінна X 5 | 0,18963 | 0,269576 | -0,70344 | 0,532461 | -1,04754 | 0,66828 |
Таблиця 2.10
Результати обчислення
| Спостереження | Предсказанное Y | Залишки |
| 1 | 3991696 | 2243,456595 |
| 2 | 795590 | -110557,3476 |
| 3 | 773361,3 | 209804,8845 |
| 4 | 738006,3 | -328965,2021 |
| 5 | 708302,6 | -69943,49296 |
| 6 | 717462,7 | 177568,7562 |
| 7 | 505339,7 | 12424,29184 |
| 8 | 705983,8 | 108413,6567 |
| 9 | 1160813 | -989,0031548 |
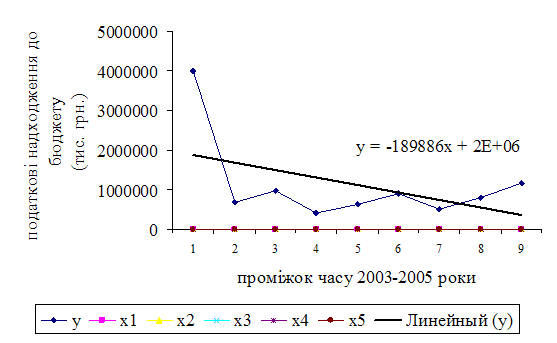
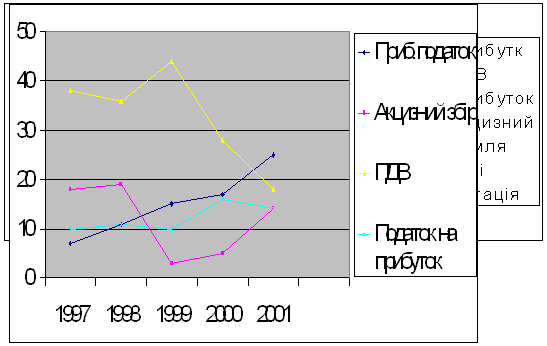
Рис. 2.8. Залежність податкових надходжень бюджету від обсягів видатків.
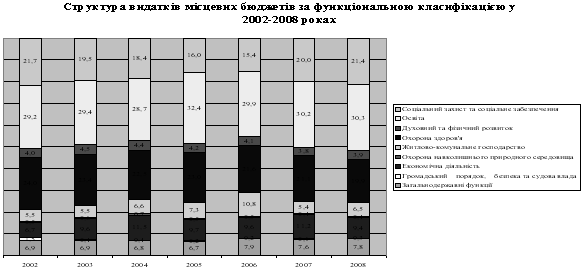
Побудована модель дає підстави дійти таких висновків. Отже протягом останніх трьох років рівень податкових надходжень зменшується, що пояснюється, як низьким рівнем доходів громадян, так і приховуванням бази оподаткування і юридичними і фізичними особами. В той же час видатки на державне управління, соціальний захист, різноманітні соціальні виплати, кошти, що сплачуються до бюджету розвитку тощо не зменшуються, а навпаки зростають і є найбільш вагомими складовими у системі видатків.
Таким чином штучно зменшена база оподаткування є основною причиною того, що податкові надходження не покривають видатки, внаслідок чого і виникає бюджетний дефіцит.
Похожие работы
... визначаються способами їх формування. Способи формування доходів, у свою чергу, зумовлені характером та особливостями економічної системи. 2. Аналіз доходів місцевих бюджетів та оцінка рівня їх забезпеченості 2.1 Сучасний стан доходів місцевих бюджетів України Місцеві бюджети виконують особливу роль у кожній унітарній країні тому, що вони є фінансовою основою місцевого самоврядування. ...
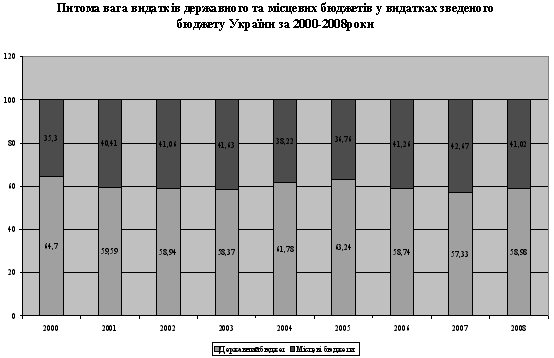
... ,2 131 061,2 59 238,7 45,2 Загальний фонд 33 876,7 47 189,0 111 059,0 52 411,6 47,2 Спеціальний фонд 5 022,5 6 038,2 20 002,2 6 827,1 34,1 Діаграма 2.7. Частка видатків місцевих бюджетів у зведеному бюджеті становила 41,3%, що на 0,3 % більше, ніж аналогічний показник 2008 року. Частка видатків загального фонду місцевих бюджетів у видатках зведеного бюджету зросла на 1,8 % і ...
... з бюджетами інших країн та для макроекономічного аналізу. На 2002 рік передбачено формування державного бюджету на основі програмно-цільового методу, а в перспективі – і місцевих бюджетів. Бюджетний процес на локальному рівні також починається із бюджетної політики, тобто заяв, зроблених політиками для конкретизації їхньої філософії фінансового управління. Після схвалення Кабінетом Міністрів ...
... ї заробіт-ної плати в Україні. Прогнозуючи лінійній характер мінімальної заробітної плати в Україні, слід очікувати наступний характер зростанні власних доходів місцевого бюджету Петропавлівського району Дніпропетровської області (табл.4.1, рис.4.5): Таблиця 4.2. Прогноз щомісячного рівня власних доходів місцевого бюджету Петропавліського району Дніпропетровської області у 2009 - 2012 роках ...

0 комментариев