Осмос, осмотическое давление. Уравнение Вант-Гоффа и осмотический коэффициент
Адсорбция ионов на твердой поверхности. Понятие об ионитах. Обратимая ионообменная адсорбция – основа ионообменной хроматографии
Коагуляция дисперсной системы. Скорость коагуляции. Причины, вызывающие процесс самопроизвольной коагуляции
Навигация
Осмос, осмотическое давление. Уравнение Вант-Гоффа и осмотический коэффициент
Вычисление теплового эффекта реакций
22315
знаков
0
таблиц
0
изображений
34. Осмос, осмотическое давление. Уравнение Вант-Гоффа и осмотический коэффициент.
Осмос – самопроизвольное движение молекул растворителя через полупроницаемую мембрану, разделяющую растворы разной концентрации, из раствора меньшей концентрации в раствор с более высокой концентрацией, что приводит к разбавлению последнего. В качестве полупроницаемой мембраны, через маленькие отверстия которой могут селективно проходить только небольшие по объему молекулы растворителя и задерживаются крупные или сольватированные молекулы или ионы, часто служит целлофановая пленка – для высокомолекулярных веществ, а для низкомолекулярных – пленка из ферроцианида меди. Процесс переноса растворителя (осмос) можно предотвратить, если на раствор с большей концентрацией оказать внешнее гидростатическое давление (в условиях равновесия это будет так называемое осмотическое давление, обозначаемое буквой ). Для расчета значения в растворах неэлектролитов используется эмпирическое уравнение Вант-Гоффа:
= C R T,
где С – моляльная концентрация вещества, моль/кг;
R – универсальная газовая постоянная, Дж/моль · К.
Величина осмотического давления пропорциональна числу молекул (в общем случае числу частиц) одного или нескольких веществ, растворенных в данном объеме раствора, и не зависит от их природы и природы растворителя. В растворах сильных или слабых электролитов общее число индивидуальных частиц увеличивается вследствие диссоциации молекул, поэтому в уравнение для расчета осмотического давления необходимо вводить соответствующий коэффициент пропорциональности, называемый изотоническим коэффициентом.
i · C · R · T,
где i – изотонический коэффициент, рассчитываемый как отношение суммы чисел ионов и непродиссоциировавших молекул электролита к начальному числу молекул этого вещества.
Так, если степень диссоциации электролита, т.е. отношение числа молекул, распавшихся на ионы, к общему числу молекул растворенного вещества, равна и молекула электролита распадается при этом на n ионов, то изотонический коэффициент рассчитывается следующим образом:
i = 1 + (n – 1) · ,(i > 1).
Для сильных электролитов можно принять = 1, тогда i = n, и коэффициент i (также больше 1) носит название осмотического коэффициента.
Явление осмоса имеет большое значение для растительных и животных организмов, поскольку оболочки их клеток по отношению к растворам многих веществ обладают свойствами полупроницаемой мембраны. В чистой воде клетка сильно набухает, в ряде случаев вплоть до разрыва оболочки, а в растворах с высокой концентрацией солей, наоборот, уменьшается в размерах и сморщивается из-за большой потери воды. Поэтому при консервировании пищевых продуктов к ним добавляется большое количество соли или сахара. Клетки микроорганизмов в таких условиях теряют значительное количество воды и гибнут.
Осмотическое давление обеспечивает движение воды в растениях за счет различия осмотических давлений между клеточным соком корней растений (5-20 бар) и почвенным раствором, дополнительно разбавляемом при поливе. Осмотическое давление обусловливает в растении подъем воды от корней до вершины. Таким образом, клетки листьев, теряя воду, осмотически всасывают ее из клеток стебля, а последние берут ее из клеток корня.
43. Рассчитать эквивалентную электропроводность 1 н раствора NaNO3, если его удельное сопротивление равно 12,42 Ом · см.
Решение.
Эквивалентная электропроводность – величина электропроводности, отнесенная к одному моль – эквиваленту электролита:
,
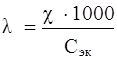где λ – эквивалентная электропроводность, Ом – 1 · см2 · моль– 1;
Сэк – молярная концентрация эквивалентов раствора электролита, моль/л.
Удельная электропроводность – величина, обратная удельному сопротивлению:
где cудельная электрическая проводимость, Ом – 1.см – 1;
ρ – удельное электрическое сопротивление, Ом · см.
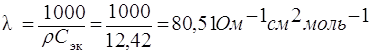
52. Отличительные признаки дисперсных систем от истинных растворов. Механизм проявления каждого отличительного признака.
Истинный раствор — это гомогенные смеси, состоящие из растворенных веществ и растворителя. В истинных растворах растворенные вещества находятся либо в молекулярно-дисперсном, либо в ионно-дисперсном состоянии.
Истинно растворимые частицы обуславливают, в частности, осмотическое давление, осмотические явления снижения температуры замерзания и повышения температуры кипения.
Высокодисперсные гетерогенные системы, в отличие от растворов, содержат чаще всего 2 фазы. Одна фаза представляет собой высокодисперсные мельчайшие частицы вещества или макромолекулы ВМС и называется дисперсной фазой. Другая фаза, в которой распределены агрегаты дисперсных частиц или макромолекул, называется дисперсионной средой. Условием образования таких дисперсных систем (коллоидного состояния вещества) является нерастворимость одной фазы в другой.
Дисперсная фаза, состоящая из множества мельчайших частиц, имеет очень большую удельную поверхность раздела с дисперсионной средой. Особые свойства поверхности раздела обусловливают специфические особенности дисперсных систем, что и является причиной выделения данной области знания в отдельную науку – коллоидную химию.
Основными отличительными особенностями дисперсных систем от истинных растворов являются:
а) способность к рассеиванию ими света;
б) медленная диффузия частиц дисперсной фазы в дисперсионной среде;
в) способность к диализу;
г) агрегативная неустойчивость дисперсной фазы, которая определяется выделением частиц из дисперсионной среды при добавлении к системе электролитов или под влиянием других внешних воздействий.
61. Рассчитать средний сдвиг частиц аэрозоля с радиусом частиц 10-7 м за время 10 с при температуре 273 К и вязкости воздуха 1,7·10-5 н·с/м2. Как изменится средний сдвиг частиц, если радиус частиц аэрозоля увеличится до 10-6 м?
Средний сдвиг частиц аэрозоля
время, за которое происходит смещение частицы (продолжительность диффузии), с;
D коэффициент диффузии, м2 . с-1.
Коэффициент диффузии для сферической частицы рассчитывается по уравнению Эйнштейна:
,
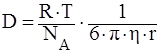где NА – число Авогадро, 6 10 23 молекул/моль;
h – вязкость дисперсионной среды, Н с/м2 (Па с);
r – радиус частицы, м;
R – универсальная газовая постоянная, 8,314 Дж/моль · К;
T – абсолютная температура, К;
число 3,14.
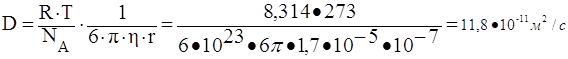
ответ на второй вопрос задания:
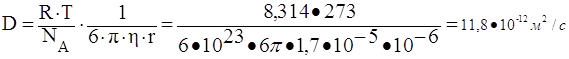
Таким образом, средний сдвиг частицы уменьшиться в 10 раз.
Ответ: 
, уменьшится в 10 раз.
Похожие работы
... от (Т – 100) до (Т + 100) К; 3. укажите, как изменяется константа равновесия при повышении температуры; 4. определите тепловой эффект реакции при Т, К; 5. сопоставьте тепловой эффект, вычисленный в п. 4, с тепловым эффектом, вычисленным по закону Кирхгофа при температуре Т, К; 6. определите стандартное сродство реагирующих веществ при температуре Т, К. ...
... условия сдвига равновесия вправо .... Глава 2. Прикладные аспекты преподавания темы «Закономерности течения химических реакций» Прикладные аспекты преподавания темы «Закономерности течения химических реакций» на мой взгляд удобнее всего рассматривать на уроках, которые следуют сразу за рассмотрением скорости реакции и химического равновесия, - это производство серной кислоты. 2.1 ...
... в уравнениях реакций и не забывать о том, что складываемые, вычитаемые или сокращаемые моли вещества должны находиться в одинаковом агрегатном состоянии. 2. Применение теплового эффекта на практике Тепловые эффекты химических реакций нужны для многих технических расчетов. Например, рассмотрим мощную российскую ракету "Энергия", способную выводить на орбиту космические корабли и другие полезные ...
... коэффициенты в уравнениях реакций и не забывать о том, что складываемые, вычитаемые или сокращаемые моли вещества должны находиться в одинаковом агрегатном состоянии. 2. Применение теплового эффекта на практике Тепловые эффекты химических реакций нужны для многих технических расчетов. Например, рассмотрим мощную российскую ракету "Энергия", способную выводить на орбиту космические корабли и ...
0 комментариев