Навигация
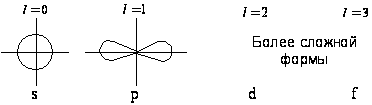
Завершая расчеты волновых функций σπ- и σπ2-гибридов, изобразим полярные диаграммы гибридных орбиталей и уровни энергии
10378
знаков
0
таблиц
4
изображения
3.3.7. Завершая расчеты волновых функций σπ- и σπ2-гибридов, изобразим полярные диаграммы гибридных орбиталей и уровни энергии.
3.3.8. Покажем, что энергия смешанного гибридного состояния отличается от энергий исходных чистых состояний и является их средневзвешенной величиной. Для расчета используем исходный гамильтониан плоского ротатора, для которого σ- π-орбитали являются собственными функциями.
Расчитывая уровни σπ- и σπ2-гибридов, мы имеем возможность продемонстрировать компактность и простоту математических выкладок, основанных на операторных уравнениях с использованием бра- и кет-символов скалярных произведений – интегралов.
Обратимся к 5-му постулату, на основании которого производится расчет средних значений динамических переменных. Энергия σπ-гибрида равна:
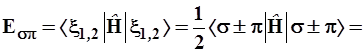
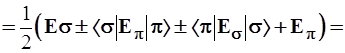
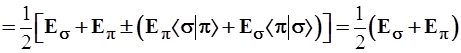. (3.59)
Уровень σπ-гибрида оказался дважды вырожденным и лежащим точно посередине между исходными уровнями σ- и π-орбиталей. При выводе использованно свойство ортонормированности базиса: ‹σ|σ›=1; ‹σ|π› = ‹π|σ› = 0
3.3.9. Энергия σπ2-гибрида рассчитывается аналогично; для краткости записи введем обозначение 
и получим:
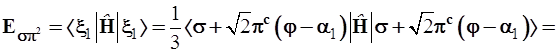
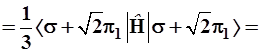
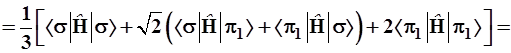
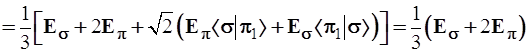(3.60)
Здесь гибридный уровень трижды вырожден и лежит ближе к π-уровню, котоpый представлен в формуле (3.60) со вдвое большим весом по сравнению с Еσ.
Информация, полученная нами в этом разделе, окажется очень полезной при качественном анализе химической. связи и теории валентности.
3.4. Совместные измерения динамических переменных. Коммутация операторов и соотношения неопределенностей Гейзенберга.
3.4.1. Вновь обратимся к анализу измерений. На основе результатов, полученных в разделах 2.2.3, 2.3.2 и 3.2.2, мы в состояниирешить очень важную проблему, связанную с совместными измерениями различных динамических переменных. Исследуем эту проблему на основе анализа операторных уравнений, имитирующих акты измерений. Последовательному измерению двух величин λ и μ соответствует произведение связанных с ними операторов 
и 
, т.е. их последовательное выполнение. Запись 
означает, что раньше измеряется величина μ, а затем λ. И, обратно, запись 
отвечает первичному измерению величины λ и затем – величины μ. Таким образом правило о последовательности выполнения операторов таково: произведение 
означает, что сначала на функцию действует оператор, стоящий непосредственно слева от функции, т.е. 
, в результате чего получается новая функция, над которой выполняется преобразование, диктуемое оператором 
.
3.4.2. Вопрос о совместности измерений двух величин сводится к тому, можно ли без последствий изменять порядок измерений. Если результаты не зависят от последовательности измерений, то операторные схемы 
и 
должны быть эквивалентными, а их разность будет нулевой:
, (3.61)
или, собирая влево от функции все операторы, получим:
.
(3.62)
Формула (3.62) называется коммутационным (перестановочным) соотношением, а разность произведений операторов, записанных в разной последовательности, носит название коммутатора
.
(3.63)
3.4.3. Коммутатор равен нулю для величин, которые могут наблюдаться одновременно. Коммутирующие операторы обладают одинаковыми наборами собственных функций. Если же коммутатор отличен от нуля, то совместное измерение величин не имеет смысла, т.е. такой прибор в принципе невозможно построить.
3.4.4. Рассмотрим одновременные измерения величин, у которых произведение их размерностей совпадает с размерностью константы Планка ([энергия]·[время]). Таковыми являются:
а) импульс и координата в одномерном поступательном движении;
б) проекция момента импульса на ось и точное положение, ротатора на орбите при плоском вращении, определяемом углом φ;
в) энергия и время у нестационарной системы.
Для этих трех случаев составим коммутаторы, пользуясь формулами (2.10), (3.24) и (2.19). На основании уравнения (2.19) оператор гамильтона 
можно заменить оператором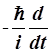 
. Получаем:
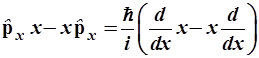, (3.64)
,
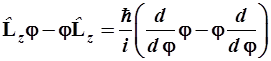(3.65)
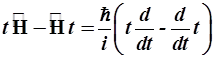(3.66)
В случае (3.66) волновая функция, на которую действует коммутатор, должна содержать временную часть.
Посмотрим, каков результат действий этих коммутаторов на волновую функцию на примере (3.64):
.
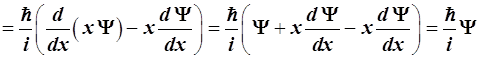Таким образом, исследуемый коммутатор 
равен
.
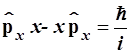(3.67)
Согласно равенству (3.67), во всех математических выражениях, где можно произвести группировку операторов 
, приводящую к коммутатору, его можно заменить мнимым числом 
. Это же справедливо и для (3.65), и (3.66). Напомним, что операторы можно выносить только влево от функции и, производя преобразования, нельзя нарушать порядок сомножителей, но допустима группировка операторных слагаемых и сомножителей. Аналогично получаем:
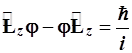, (3.68)
.
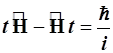(3.69)
Формулы (3.67), (3.68) и (3.69) дают строгие операторные выражения принципа неопределенностей Гейзенберга, запрещающего одновременное точное измерение перечисленных пар переменных, и это принципиальное ограничение не связано с конструкцией прибора.
Похожие работы
... детерминант и диаграмма уровней. Хюккелевский детерминант треугольного цикла. X 1 1 1 X 1 = 0; ® X3+2-3X=0; ® X1,2,3= -2; +1; +1; ® E1,2,3=+2 1 X два решения одинаковы – уровень дважды вырожден Молекулярные орбитали дважды-вырожденного уровня треугольного цикла. Базисные АО =2p(C) j1=(p1+p2+p3)/31/2 невырожденный уровень AСвязывающий основной j2=(p1+p2-2p3)/61/2 j3=(p1-p2)/21/2 ...
... с кислородом, восстановлением - отнятие кислорода. С введением в химию электронных представлений понятие окислительно-восстановительных реакций было распространено на реакции, в которых кислород не участвует. В неорганической химии окислительно-восстановительные реакции (ОВР) формально могут рассматриваться как перемещение электронов от атома одного реагента (восстановителя) к атому другого ( ...
... различия в природе связей между атомами углерода ( боковое перекрывание, прочность, доступность для реагентов), проводит сравнение с одинарной С-С связью в этане ( длина связи 0,154 нм). Третье валентное состояние атома углерода. Учитель, говорит, что существуют органические вещества, в которых атом углерода связан только с двумя соседними атомами. Это ацетилен. В этом соединении атомы углерода ...
... . (фторид натрия состоит из ионов натрия Na+ и фторид-ионов F-) Если разность электроотрицательностей атомов велика, то электронная пара, осуществляющая связь, переходит к одному из атомов, и оба атома превращаются в ионы. Химическая связь между ионами, осуществляемая за счет электростатического притяжения, называется ионной связью. Водородная связь. Водородная связь - зто связь между ...
0 комментариев