Навигация
Выбор разрешающего столбца. В качестве разрешающего выбираем столбец с минимальным коэффициентом в строке f(x). В данном примере это столбец х2
1. Выбор разрешающего столбца. В качестве разрешающего выбираем столбец с минимальным коэффициентом в строке f(x). В данном примере это столбец х2.
2. Выбор разрешающей строки. Для выбора разрешающей строки (разрешающего элемента) среди положительных коэффициентов разрешающего столбца выбираем тот элемент, для которого отношение коэффициентов в столбце свободных членов к коэффициенту в разрешающем столбце минимально. Разрешающий элемент рассчитывается по формуле:
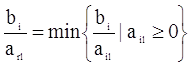
В данном примере такой строкой будет строка х3, т.к. отношение коэффициента в столбце свободных членов к коэффициенту в разрешающем столбце минимально.
3. Замена базиса. Для перехода к следующей симплексной таблице (следующему опорному плану с большим значением целевой функции) делаем шаг модифицированного жорданова исключения с разрешающим элементом arl, при котором базисная переменная xr становится свободной и одновременно свободная переменная xi становится базисной.
3.1 на месте разрешающего элемента ставится 1 и делится на разрешающий элемент;
3.2 остальные элементы разрешающего столбца меняют знак на противоположный и делятся на разрешающий элемент;
3.3 остальные элементы разрешающей строки делятся на разрешающий элемент;
3.4. все остальные элементы симплексной таблицы вычисляются по формуле:
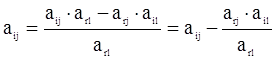
3.5. элементы правого столбца и нижней строки пересчитываются по тому же принципу, что и элементы в центральной части таблицы.
Симплексная таблица, рассчитанная по алгоритму:
Таблица 2.
| -х1 | -х3 | ||
| х2 = | 0,067 | 0,3 | 6 |
| х4 = | 0,57 | -0,67 | 1,1 |
| х5 = | 2,17 | -0,67 | 11 |
| f(x) = | -3,27 | 1,3 | 72,6 |
Следующим разрешающим столбцом будет столбец х1, а разрешающей строкой – х4. Далее действуем по тому же алгоритму.
Таблица 3.
| -х4 | -х3 | 1 | |
| х2 = | -0,1 | 0,24 | 5,87 |
| х1 = | 1,75 | -1,17 | 1,03 |
| х5 = | -3,8 | 1,88 | 5,8 |
| f(x) = | 5,7 | -2,5 | 35,06 |
Следующим разрешающим столбцом будет столбец х5, а разрешающей строкой – х3. Далее действуем по тому же алгоритму.
Таблица 4.
| -х4 | -х5 | 1 | |
| х2 = | 0,39 | -0,13 | 4,4 |
| х1 = | -0,61 | 0,6 | 6,19 |
| Х3 = | -2 | 0,53 | 1,3 |
| f(x) = | 0,64 | 1,3 | 36,08 |
Конечная симплексная таблица:
Все коэффициенты в строке целевой функции положительны, т.е. мы нашли оптимальное решение.
Таким образом, в точке x1 = 4, x2 = 6, x3 = 1,3, x4 = 0, x5 = 0 целевая функция принимает максимальное значение f(x) = 36.
При этом переменным, которые стоят в верхней строке, в базисном решении присваивается значение 0 – это свободные переменные. Каждая из переменных, стоящая в левом столбце, приравнивается к числу, записанному в правом столбце той же самой строки – это базисные переменные.
Постановка двойственной задачи ЛП. Определить значение двойственных оценок можно следующим образом. если некоторый i-тый ресурс используется не полностью, т.е. имеется резерв, значит дополнительная переменная в ограничении для данного ресурса будет больше нуля. Очевидно, что при увеличении общего машинного времени не произошло бы увеличение целевой функции. Следовательно, машинное время не влияет на прибыль и для третьего ограничения двойственная переменная y3 = 0. Таким образом, если по данному ресурсу есть резерв, то дополнительная переменная будет больше нуля, а двойственная оценка данного ограничения равна нулю.
В данном примере оба вида сырья использовались полностью, поэтому их дополнительные переменные равны нулю (в итоговой симплексной таблице переменные х3 и х4 являются свободными, значит х3 = х4 = 0). Если ресурс использовался полностью, то его увеличение или уменьшение повлияет на объем выпускаемой продукции и, следовательно, на величину целевой функции. Значение двойственной оценки при этом находится в симплекс-таблице на пересечении строки целевой функции со столбцом данной дополнительной переменной.
![]()
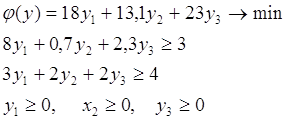
Получить решение двойственной задачи из полученной ранее симплексной таблицы и произвести анализ полученных результатов. Формулировка и результаты решения исходной и двойственной задач распределения ресурсов приведены в таблице 4.
Таблица 4.
| Исходная задача ЛП | Двойственная задача ЛП | ||||||||||||||||||||
| Математическая постановка | |||||||||||||||||||||
|
|
| ||||||||||||||||||||
| Обозначения и интерпретация параметров задачи | |||||||||||||||||||||
| xj, j = f(x) – общая прибыль от реализации продукции | yi, i =
| ||||||||||||||||||||
| Экономическая интерпретаци язадачи | |||||||||||||||||||||
| Сколько и какой продукции необходимо произвести, чтобы пр заданных стоимостях cj, j = | Какова должна быть цена единицы каждого из ресурсов, чтобы при заданных их количествах bi, i = | ||||||||||||||||||||
| Результаты решения | |||||||||||||||||||||
| Результирующая симплекс-таблица
Основные переменные х1 = 6,19 х2 = 4,4 дополнительные переменные х3 = 1,3 х4 = 0 х5 = 0 | Дополнительные переменные y4 = 0 y5 = 0 основные переменные y1 = 0,64 y2 = 1,3 y3 = 0 | ||||||||||||||||||||
| Интерпретация дополнительных переменных | |||||||||||||||||||||
| xn+1, …., xn+m – неиспользованное (резервное) количество соответствующего ресурса (при наличие резервного ресурса соответствующая двойственная переменная навна 0) | ym+1, …, ym+n – насколько уменьшится целевая функция при принудительном выпуске единицы данной продукции (если какая-либо из основных переменных исходной задачи равна 0) | ||||||||||||||||||||
Проверить результаты решения в табличном процессоре Excel. В Excel имеется надстройка «Поиск решения», которая позволяет решать оптимизационные задачи.
Использовав эту надстройку для решения нашей задачи ЛП, получаем следующий результат:
Таблица 6.
| Переменные | Целевая функция | ||||
| Вид продукции | Р1 | Р2 | Прибыль | ||
| Значение | 6,1875 | 4,3844 | 36,1 | ||
| Прибыль от ед. прод. | 3 | 4 | макс | ||
| Ограничения | |||||
| Типы ресурсов | Р1 | Р2 | Расход ресурсов | Знак | Запас ресурсов |
| Сырье S1 | 0,2 | 3 | 14,390625 | <= | 18 |
| СырьеS2 | 0,7 | 2 | 13,1 | <= | 13,1 |
| Машинное время | 2,3 | 2 | 23 | <= | 23 |
Но при применении надстройки «поиск решения» к задаче, двойственной данной задаче ЛП, приходим к выводу, что решение полученное с помощью надстройки не сходится с решением из симплекс-таблицы:
Таблица 7.
| Переменные |
| ||||||
| имя | x1 | x2 | f(x) |
| |||
| значение | 6,19 | 4,38 | 36,1 |
| |||
| коэф-ты f(x) | 3 | 4 | макс |
| |||
| Ограничения | двойств. Оценки | ||||||
| № | x1 | x2 | левая часть | знак | правая часть | y | |
| 1 | 8 | 3 | 62,653125 | <= | 18 | 1,333333 | |
| 2 | 0,7 | 2 | 13,1 | <= | 13,1 | 0 | |
| 3 | 2,3 | 2 | 23 | <= | 23 | 0 | |
| Ограничения двойственной задачи | Целевая функция двойственной задачи | ||||||
| 10,66667 | 4 | 24 | |||||
Лабораторная работа № 2 (Решение задачи ЛП средствами табличного процессора Excel)
Для заданной содержательной постановки задачи ЛП выполнить следующие действия:
Осуществить математическую запись задачи ЛП;
Решить задачу с использование надстройки Excel «Поиск решения»;
Привести математическую постановку двойственной задачи ЛП;
Получить решение двойственной задачи ЛП с использованием надстройки Excel «Поиск решения»;
Получить решение задачи в предположении целочисленности переменных;
Произвести анализ полученных результатов и дать их содержательную интерпретацию.
Задача: В состав рациона кормления входят три продукта: сено, силос и концентраты, содержащие следующие питательные вещества: белок, кальций и витамины. Содержание питательных веществ в граммах в 1 килограмме соответствующего продукта питания и минимально необходимое их потребление заданы таблицей:
| Продукты | Питательные вещества | ||
| белок | кальций | витамины | |
| 1. Сено | 5 | 6 | 2 |
| 2. Силос | 2 | 4 | 1 |
| 3. Концентраты | 18 | 3 | 1 |
| Норма потребления | 200 | 120 | 40 |
Определить оптимальный режим кормления, из условия минимальной стоимости, если цена 1 кг продукта питания соответственно составляет: для сена - 30коп., для силоса- 20 коп., для концентрата – 50 коп.
Решение
Осуществить математическую запись задачи ЛП. Составим математическую модель. Обозначим через х1 – количество единиц сена, через х2 – количество единиц силоса а через х3 – количество единиц концентрата. Функция затрат на покупку этих продуктов выглядит так: f(x)=30x1+20x2+50x3 её необходимо минимизировать. Необходимые нормы потребления выражены в виде ограничений:
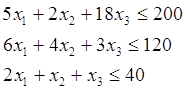
В результате общая постановка задачи ЛП имеет вид:
![]()
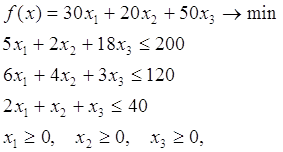
Решить задачу с использование надстройки Excel «Поиск решения». В качестве значений переменных выступает количество закупаемой продукции каждого вида. В ячейках «Расход питательных веществ» содержатся формулы, определяющие левые части ограничений, а в ячейках необходимое потребление питательных веществ – значения правых частей ограничений.
После ввода всех данных выбираем команду Сервис / Поиск Решения и, заполняем открывшееся диалоговое окно Поиск Решения:
В качестве целевой ячейки выбираем ячейку, в которой находится значение целевой функции, выполняем максимизацию функции, изменяя ячейки со значениями количества продукции. Устанавливаем ограничения.
Далее выбираем пункт «Параметры», чтобы проверить, какие параметры заданы для поиска решения. В окне Параметры поиска решения можно изменять условия и варианты поиска решения исследуемой задачи, а также загружать и сохранять оптимизируемые модели.
Для данной задачи достаточно установить два флажка «Линейная модель» (т.к. ограничения и целевая функция являются линейными по переменным) и «Неотрицательные значения» (для выполнения условий ![]() задачи ЛП).
задачи ЛП).
Теперь задача оптимизации подготовлена полностью. После нажатия кнопки «Выполнить» открывается окно «Результаты поиска решения», которое сообщает, что решение найдено.
Таблица 9
|
Переменные | Целевая функция | |||||
| Вид продукта | сено | силос | концентрат | f(x) | ||
| значение | 16,77 | 0,00 | 6,45 | 76,13 | ||
| затраты на ед.прод. | 3 | 2 | 4 | min | ||
| Ограничения | ||||||
| Питательные вещества | сено | силос | концентрат | расход питательных веществ | знак | необходимое потребление пит.веществ |
| белки | 5 | 2 | 18 | 200,00 | >= | 200 |
| кальций | 6 | 4 | 3 | 120,00 | >= | 120 |
| витамины | 2 | 1 | 1 | 40,00 | >= | 40 |
Привести математическую постановку двойственной задачи ЛП. Двойственная задача ЛП определяется по формуле:
![]()
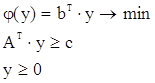
Математическая постановка двойственной задачи ЛП:
![]()
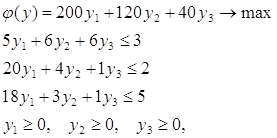
Получить решение двойственной задачи ЛП с использованием надстройки Excel «Поиск решения». К имеющимся данным добавляются значения двойственных переменных, ячейка, содержащая формулу целевой функции двойственной задачи, и ячейки, определяющие левые части ограничений двойственной задачи. Далее для решения двойственной задачи выполняем с помощью надстройки Excel «Поиск решения». Получаем:
Таблица 10
| Переменные | Целевая функция |
| |||||
| Вид продукта | сено | силос | концентрат | f(x) |
| ||
| значение | 16,77 | 0,00 | 6,45 | 76,13 |
| ||
| затраты на ед.прод. | 3 | 2 | 4 | min |
| ||
| Ограничения | |||||||
| Питательные вещества | сено | силос | концентрат | Левая часть | знак | Правая часть | Двойственные оценки |
| белки | 5 | 2 | 18 | 200,00 | >= | 200 | 0,6 |
| кальций | 6 | 4 | 3 | 120,00 | >= | 120 | 0 |
| витамины | 2 | 1 | 1 | 40,00 | >= | 40 | 0 |
| Ограничения двойственной функции | Целевая функция двойственной задачи | ||||||
| 3 | 1,2 | 10,8 | 120 | ||||
Получить решение задачи в предположении целочисленности переменных/ Для решения поставленной задачи воспользуемся командой Поиск решения. К исходным данным при решении задачи ЛП добавим еще одно ограничение целочисленности для ячеек, содержащих искомое количество производимой продукции. После выполнения поиска получаем решение, приведенное в таблице 11.
Таблица 11
| Переменные | Целевая функция | |||||
| Вид продукта | сено | силос | концентрат | f(x) | ||
| значение | 16 | 0 | 6 | 76 | ||
| затраты на ед.прод. | 3 | 2 | 4 | min | ||
| Ограничения | ||||||
| Питательные вещества | сено | силос | концентрат | расход питательных веществ | знак | необходимое потребление питательных веществ |
| белки | 5 | 2 | 18 | 200 | >= | 200 |
| кальций | 6 | 4 | 3 | 120 | >= | 120 |
| витамины | 2 | 1 | 1 | 40 | >= | 40 |
Из полученного решения очевидно, что для минимизации затрат необходимо закупать 16 кг сена и 6 кг концентрата, закупка же силоса нецелесообразна. При этом потребление питательных веществ, таких как – белок, кальций и витамины не уменьшится.
Лабораторная работа № 3 (Решение транспортной задачи)
Для заданной матрицы издержек С, вектора – столбца запасов В в пунктах отправления и вектора - строки потребностей А в пунктах назначения решить транспортную задачу и составить отчет по следующим пунктам:
Осуществить математическую запись транспортной задачи;
Решить задачу с помощью надстройки Excel «Поиск решения»;
Изменить данные для получения открытой задачи и решить ее.
 2 3 4 2 4 140
2 3 4 2 4 140
С= 8 4 1 4 1 180
9 7 3 7 2 160
60 70 120 130 100
Решение
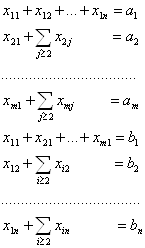
Осуществить математическую запись транспортнойзадачи.Обозначим через хij количество единиц сырья, перевозимого из i-го пункта его получения на j-тое предприятие. Тогда условие доставки и вывоза необходимого и имеющегося сырья обеспечиваются за счет выполнения следующих равенств:
![]() x11+x12+x13+x14+x15 =140
x11+x12+x13+x14+x15 =140
x21+x22+x23+x24+x25 =180
x31+x32+x33+x34+x35 =160
x11 +x21 +x31 =60
x 12 +x22 +x32 =70
x 13 +x23 +x33 =120
x 14 +x24 +x34 =130
x 15 +x25 +x35=100
При этом общая стоимость перевозок составит
f(x)= 2x11+3x12+4x13+2x14+4x15 +8 x21+4x22+x23+4x24+x25+9 x31+7x32+3x33+7x34+2x35
Таким образом, математическая постановка данной транспортной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений, при котором целевая функция f(x) принимает минимальное значение.
Решить задачу с помощью надстройки Excel «Поиск решения». Находим оптимальный план поставок сырья и соответствующие ему транспортные расходы в таблице 12.
Таблица 12
| Пункты отправления | Пункты назначения | |||||
| В1 | В2 | В3 | В4 | В5 | Запасы | |
| А1 | 2 | 3 | 4 | 2 | 4 | 140 |
| А2 | 8 | 4 | 1 | 4 | 1 | 180 |
| А3 | 9 | 7 | 3 | 7 | 2 | 160 |
| Потребности | 60 | 70 | 120 | 130 | 100 | |
| Транспортная таблица | ||||||
| А1 | 140 | 0 | 0 | 0 | 0 | 140 |
| А2 | 0 | 0 | 180 | 0 | 0 | 180 |
| А3 | 0 | 0 | 0 | 0 | 160 | 160 |
| Потребности | 60 | 70 | 120 | 130 | 100 | |
| Транспортные расходы | 780 | |||||
Изменим, данные для того, чтобы получить открытую задачу. Для этого уменьшим запасы и увеличим потребности, получим:
Таблица 13
| Таблица издержек | ||||||
| Пункты отправления | Пункты назначения | |||||
| В1 | В2 | В3 | В4 | В5 | Запасы | |
| А1 | 2 | 3 | 4 | 2 | 4 | 140 |
| А2 | 8 | 4 | 1 | 4 | 1 | 150 |
| А3 | 9 | 7 | 3 | 7 | 2 | 100 |
| Потребности | 60 | 100 | 120 | 200 | 100 | |
| Транспортная таблица | ||||||
| А1 | 0 | 0 | 0 | 140 | 0 | 140 |
| А2 | 0 | 0 | 0 | 0 | 150 | 150 |
| А3 | 0 | 0 | 0 | 0 | 100 | 100 |
| Потребности | 60 | 100 | 120 | 200 | 100 | |
| Транспортные расходы | 630 | |||||
Лабораторная работа №4 (решение задач нелинейного программирования)
Для заданной математической постановки задачи НП (целевой функции f(x) и ограничений - равенств) выполнить следующие действия:
Найти все условные экстремумы функций методом множителей Лагранжа и выбрать среди них глобальный минимум (максимум);
Проверить результаты решения в табличном процессоре Excel;
![]()
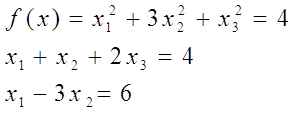 (1)
(1)
Метод множителей Лагранжа
Необходимо перевести условие к виду
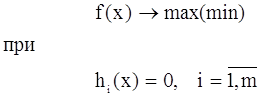
Составим вспомогательную функцию Лагранжа:
![]()
Для данной задачи получим:
![]() (2)
(2)
Дифференцируем данную функцию по х1, х2, x3, ![]() и
и ![]() , получим систему уравнений:
, получим систему уравнений:
![]()
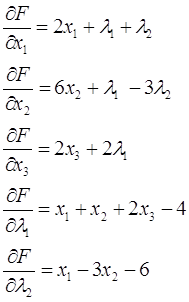 (3)
(3)
Как известно, для того, чтобы найти экстремум функции многих переменных (если он вообще существует) необходимо приравнять к нулю все его частные производные и решить полученную систему уравнений.
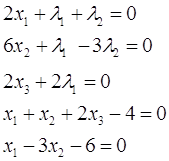
![]()
Решив это уравнение, получаем:
х1=2,25, х2=-1,25, x3= 1,5, ![]() =-1,5 и
=-1,5 и ![]() =-3, F=12
=-3, F=12
Точка экстремума заданной функции f(x) - (х1, х2, x3), является точкой глобального минимума при заданных ограничениях функции.
Решение в табличном процессоре Excel. Проверим результаты решения в табличном процессоре Excel.
Решение задачи с помощью процессора Excel дало следующие результаты:
Таблица 13
| х1 | х2 | x3 | |
| 2,25 | -1,25 | 1,50 | |
| Целевая функция | 12,00 | ||
| Ограничения | 4,00 | = | 4 |
| 6,00 | = | 6 |
Решения задачи обеими методами дали одинаковый результат.
Лабораторная работа №5 (задача динамического программирования об оптимальном распределении инвестиций)
Задача
Имеются четыре предприятия, между которыми необходимо распределить 100 тыс. усл.ед. средств. Значения прироста выпуска продукции на предприятиях в зависимости от выделенных средств X представлены в таблице. Составить оптимальный план распределения средств, позволяющий максимизировать общий прирост выпуска продукции.
Таблица 14
| X | g1 | g2 | g3 | g4 |
| 0 | 0 | 0 | 0 | 0 |
| 20 | 14 | 17 | 22 | 20 |
| 40 | 26 | 20 | 21 | 33 |
| 60 | 35 | 32 | 37 | 46 |
| 80 | 52 | 61 | 67 | 30 |
| 100 | 61 | 72 | 58 | 42 |
Решение
Этап I. Условная оптимизация.
Шаг 1. k = 4. Предполагаем, что все средства 100 ден.ед. переданы на инвестирование четвертого предприятия. В этом случае максимальная прибыль составит F4(C4)= 46, данные представлены в таблице 15.
Таблица 15.
| C4 | x4 | F4(C4) | X* | |||||
| 0 | 20 | 40 | 60 | 80 | 100 | |||
| 0 | 0 | - | - | - | - | - | 0 | 0 |
| 20 | - | 20 | - | - | - | - | 20 | 20 |
| 40 | - | - | 33 | - | - | - | 33 | 40 |
| 60 | - | - | - | 46 | - | - | 46 | 60 |
| 80 | - | - | - | - | 30 | - | 30 | 80 |
| 100 | - | - | - | - | - | 42 | 42 | 100 |
Шаг 2. k = 3. Определяем оптимальную стратегию инвестирования в третье и четвертое предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
![]() .
.
На его основании рассчитываются данные таблицы 16
Таблица 16.
| C3 | X3 | F3(C3) | X* | |||||
| 0 | 20 | 40 | 60 | 80 | 100 | |||
| 0 | 0+0 | - | - | - | - | - | 0 | 0 |
| 20 | 0+20 | 22+0 | - | - | - | - | 22 | 20 |
| 40 | 0+33 | 22+20 | 21+0 | - | - | - | 42 | 20 |
| 60 | 0+46 | 22+33 | 21+20 | 37+0 | - | - | 55 | 20 |
| 80 | 0+30 | 22+46 | 21+33 | 37+20 | 67+0 | - | 68 | 20 |
| 100 | 0+42 | 22+30 | 21+46 | 37+33 | 67+20 | 58+0 | 87 | 20 |
Шаг 3. k = 2. Определяем оптимальную стратегию инвестирования во второе и третье предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
![]() .
.
На его основании рассчитываются данные таблицы 3.
Таблица 17.
| C2 | X2 | F2(C2) | X* | |||||
| 0 | 20 | 40 | 60 | 80 | 100 | |||
| 0 | 0+0 | - | - | - | - | - | 0 | 0 |
| 20 | 0+22 | 17+0 | - | - | - | - | 22 | 0 |
| 40 | 0+42 | 17+22 | 20+0 | - | - | - | 42 | 0 |
| 60 | 0+55 | 17+42 | 20+22 | 32+0 | - | - | 59 | 20 |
| 80 | 0+68 | 17+55 | 20+42 | 32+22 | 61+0 | - | 72 | 20 |
| 100 | 0+87 | 17+68 | 20+55 | 32+42 | 61+22 | 72+0 | 87 | 0 |
Шаг 4. k = 1. Определяем оптимальную стратегию инвестирования в первое и остальные предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид:
![]() .
.
На его основе находятся данные таблицы 4.
Таблица 18.
| C1 | X1 | F1(C1) | X* | |||||
| 0 | 20 | 40 | 60 | 80 | 100 | |||
| 0 | 0+0 | - | - | - | - | - | 0 | 0 |
| 20 | 0+48 | 14+0 | - | - | - | - | 22 | 0 |
| 40 | 0+93 | 14+48 | 26+0 | - | - | - | 42 | 0 |
| 60 | 0+135 | 14+93 | 26+48 | 35+0 | - | - | 59 | 0 |
| 80 | 0+149 | 14+135 | 26+93 | 35+48 | 52+0 | - | 72 | 0 |
| 100 | 0+160 | 14+149 | 26+135 | 35+93 | 52+48 | 61+0 | 87 | 0 |
По данным последней таблицы максимальных доход с четырех предприятий составил 87 д.ед. При этом первое и второе предприятия не принесут никакого дохода, в них нецелесообразно вкладывать инвестиции. В 3-е предприятие нужно вложить 80 д.ед. В 4-е предприятие нужно вложить 20 д.ед. В итоге останется 20-Получается, что оптимальный план Х*(0;0;80;20)
Лабораторная работа №5 (задача динамического программирования о выборе оптимального пути в транспортной сети)
Задача
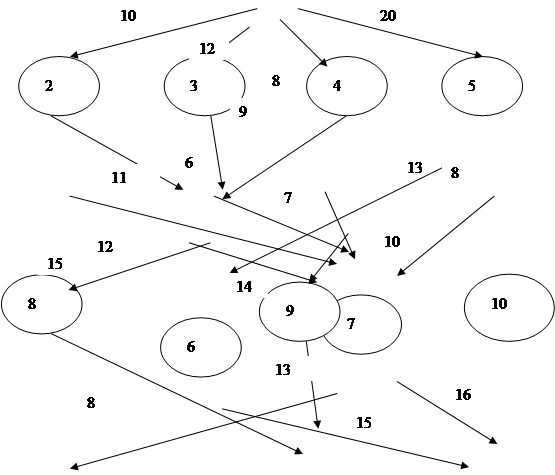
В предложенной из начального пункта (1) в конечный пункт (11). Стоимость проезда между отдельными пунктами транспортной сети придумать самостоятельно и транспортной сети имеется несколько маршрутов по проезду представить в соответствующей таблице (T(i,j)). Необходимо определить оптимальный маршрут проезда из пункта 1 в пункт 11 с минимальными транспортными расходами.
 | |||||
 | |||||
| |||||
Рисунок 2 – Транспортная сеть
Элементы матрицы маршрутов транспортной сети, а так же стоимость проезда из пункта i в пункт j (tij) представлена в таблице 19.
Таблица 19.
| j i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | - | 10 | 12 | 8 | 20 | - | - | - | - | - | - |
| 2 | - | - | - | - | - | 15 | 11 | - | - | - | - |
| 3 | - | - | - | - | - | 6 | 9 | - | - | - | - |
| 4 | - | - | - | - | - | 7 | 10 | - | - | - | - |
| 5 | - | - | - | - | - | 13 | 8 | - | - | - | - |
| 6 | - | - | - | - | - | - | - | 12 | 14 | 18 | - |
| 7 | - | - | - | - | - | - | - | 13 | 15 | 16 | - |
| 8 | - | - | - | - | - | - | - | - | - | - | 8 |
| 9 | - | - | - | - | - | - | - | - | - | - | 10 |
| 10 | - | - | - | - | - | - | - | - | - | - | 10 |
| 11 | - | - | - | - | - | - | - | - | - | - | - |
Решение
Этап I. Условная оптимизация.
Шаг 1. k = 1. F1(S) = ts10.
Таблица 18.
| S | J=11 | F(S) | J* |
| 8 | 8 | 8 | 11 |
| 9 | 10 | 10 | 11 |
| 10 | 10 | 10 | 11 |
Шаг 2. k = 2. Функциональное уравнение на данном шаге принимает вид:
![]() .
.
Результаты расчета по приведенной формуле приведены в таблице:
Таблица 19.
| S | J=8 | J=9 | J=10 | F(S) | J* |
| 6 | 12+8 | 14+10 | 18+10 | 20 | 8 |
| 7 | 13+8 | 15+10 | 16+10 | 21 | 8 |
Шаг 3. k = 3. Функциональное уравнение на данном шаге принимает вид:
![]() .
.
Результаты расчета по приведенной формуле приведены в таблице:
Таблица 20.
| S | J=6 | J=7 | F(S) | J* |
| 2 | 15+20 | 11+21 | 32 | 7 |
| 3 | 6+20 | 9+11 | 26 | 6 |
| 4 | 7+20 | 10+21 | 27 | 6 |
| 5 | 13+20 | 8+21 | 29 | 7 |
Шаг 4. k = 4. Функциональное уравнение на данном шаге принимает вид:
![]() .
.
Результаты расчета по приведенной формуле приведены в таблице:
Таблица 21.
| S | J=2 | J=3 | J=4 | J=5 | F(S) | J* |
| 1 | 10+32 | 12+26 | 8+27 | 20+29 | 35 | 4 |
Этап II. Безусловная оптимизация.
На этапе условной оптимизации получено, что минимальные затраты на проезд из пункта 1 в пункт 11 составляют F4(1) = 35, что достигается следующим движением по магистралям. Из пункта 1 следует направиться в пункт 4, затем из него в пункт 6, затем в пункт 8 и из него в пункт 11. Таким образом, оптимальный маршрут будет J*(1;4;6;8;11)
Заключение
В курсовой работе были рассмотрены решения задач нелинейного программирования, линейного программирования, динамического программирования.
Для решения задачи линейного программирования были использованы следующие методы:
1.Графический метод;
2.Симплексный метод;
3.Постановка двойственной задачи;
4.Решение задачи в предложении целочисленности переменных;
Для решения задачи нелинейного программирования были использованы следующие методы:
1.Метод множителей Лагранжа
Для решения задачи динамического программирования были использованы следующие методы:
Метод об оптимальном распределении инвестиций;
Метод выбора стратегии обновления оборудования;
Метод выбора оптимального пути в транспортной сети.
Список литературы
1.Динамическое программирование: Рек к выполнению лаб. и практ.работ / Сост.: Шипилов С.А: НФИ КемГУ.- 2-е изд.перераб.- Новокузнецк. 2002.-19 с.
2.Динамическое программирование. Шипилов С.А.
3.Методы условной оптимизации: Рек. к выполнению лаб. и практ.работ / Сост.: Шипилов С.А: НФИ КемГУ.- 2-е изд.перераб.- Новокузнецк. 2002.-48 с.
Похожие работы
... рулонов, при котором все поступающие специальные заявки будут выполнены при минимальных затратах бумаги. Графический метод решения задач линейного программирования 1. Область решений линейных неравенств. Пусть задано линейное неравенство с двумя переменными и (1) Если величины и рассматривать как координаты точки плоскости, то совокупность точек ...
... имеет вид найти переменные задачи удовлетворяющие системе ограничений: и условию неотрицательности 0 (j = ), которая обеспечивает экстремум целевой функции Z(Y) = Допустимым решением задачи линейного программирования называется любой набор значений переменных удовлетворяющий системе ограничений и условной неотрицательности. Множество допустимых решений образует область допустимых ...
... , является линейной функцией переменных : (2.4) Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без ...
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
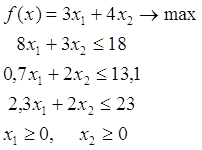
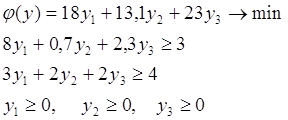

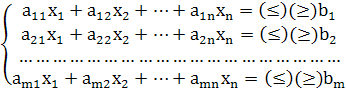
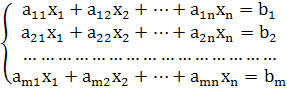



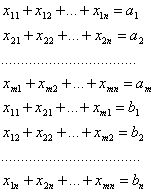



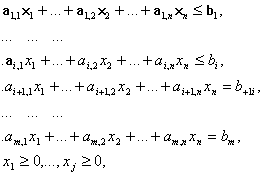
0 комментариев