Умова паралельності та перпендикулярності двох прямих, двох площин, прямої та площини у просторі

3.  Умова паралельності та перпендикулярності двох прямих, двох площин, прямої та площини у просторі.

Нехай є дві площини

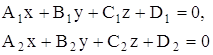(9)

З’ясуємо, за яких умов ці площини : а) паралельні; б) перепендикулярні.

Оскільки A₁,B₁,C₁ –координати вектора  , що перпендикулярний першій площині, а A₂,B₂,C₂ –координати вектора  , що перпендикулярний другій площині, то площини паралельні, якщо вектори ,  паралельні, тобто якщо їх координати пропорціональні:

.

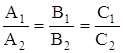Ця умова разом з тим достатня для паралельності площин ,якщо вони не співпадають.

Для того, щоб площини (9) були перпендикулярні, необхідно та достатньо, щоб вказані вектори ,  були перпендикулярні, що для ненульових векторів еквівалентно умові:

або А₁А₂+ В₁В₂+ С₁С₂=0.

Приклад. Нехай задано дві площини:

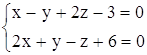
Треба з’ясувати їх взаємне розташування. В даному випадку маємо:

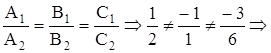 площини не паралельні.

1*2-1*1-2*1=-1 площини не перпендикулярні.

Таким чином, площини розташовані під деяким углом, відмінним від ноля та дев’яноста градусів.

Нехай є площина та пряма, задані рівняннями:

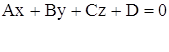
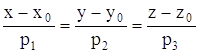
Оскільки вектор перпендикулярний площині, а вектор паралельний прямій, то пряма та площина паралельні, якщо ці вектори перпендикулярні, тобто якщо

 (10)

Якщо при цьому точка ( x₀, y₀,z₀), що належить прямій, задовольняє рівнянню площини

то пряма розташована у площині.

Пряма та площина перпендикулярні, якщо вектори  та  паралельні, тобто якщо

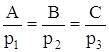 (11)

Нехай дві прямі задані рівняннями в канонічній формі:

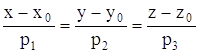(12)

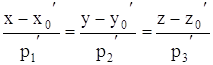 (13)

Оскільки вектор паралельний першій прямій, а вектор паралельний другій прямій, то прямі паралельні якщо

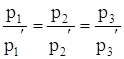
Зокрема, прямі співпадають, якщо при цьому точка першої прямої, наприклад (x₀,y₀,z₀) задовольняє рівнянню другої прямої, тобто якщо

.

Прямі перпендикулярні ,якщо вектори  та  перпендикулярні, тобто якщо

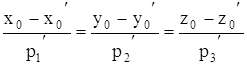Приклад. Нехай задано площину та пряму:

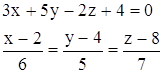
Треба з’ясувати їх взаємне розташування.

Розв’язання. Маємо:

  площина та пряма не паралельні;

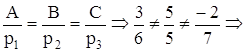 площина та пряма не перпендикулярні.

Таким чином, площина та пряма розташовані у просторі під деяким кутом, відмінним від ноля та дев’яноста градусів.