Навигация
1. Дайте определение алгебраического дополнения элемента определителя. Приведите пример вычисления алгебраического дополнения элемента а12 определителя 3-го порядка
Алгебраическим дополнением Аij элемента аij определителя n‑го порядка называется минор этого элемента, взятый со знаком (-1)i+j, где i+j – сумма номеров строки и столбца, которым принадлежит элемент аij. Т.е. по определению Аij=(-1)i+j Мij.
Для определителя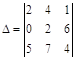 
найти алгебраические дополнения элементов а12.
Для элемента а12 i=1, j=2 и i+j=3 число нечетное, отсюда 
2. Разложите по теореме Лапласа определитель третьего порядка, записанный в общем виде по элементам второй строки
Вычисляем определитель путем разложения его по 2-ей строке
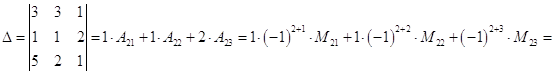
3. Какая система линейных алгебраических уравнений называется неоднородной? Какое решение имеет система неоднородных линейных уравнений, если главный определитель не равен нулю?
Система уравнений называется неоднородной, если хотя бы один свободный член уравнения не равен нулю.
Если главный определитель системы n уравнений с n неизвестными не равен нулю, то система имеет единственное решение, корни которого определяются по формулам:
, 
, …, 
4. Дайте определение матрицы и ее размера. Приведите пример матриц размеров: 1х3, 3х4,1х1.
Матрицей называется таблица чисел или каких-либо других элементов, содержащая m строк и n столбцов.
Общий вид матрицы
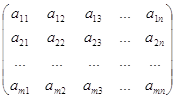
Матрица имеет размер, который определяется ее количеством строк и столбцов, что записывается так – Аm´n.
Например, числовая матрица размером 1´1 имеет вид 
, размером 1´3 имеет вид 
, размером 3´4 имеет вид 
.
5. Что такое союзная или присоединенная матрица? Приведите пример вычисления союзной матрицы для заданной.
Если для заданной квадратной матрицы А определить алгебраические дополнения всех ее элементов и затем транспонировать их, то полученная таким образом матрица будет называться союзной или присоединенной по отношению к матрице А и обозначаться символом Ã
Для матрицы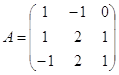 
найти Ã.
Составляем определитель матрицы А
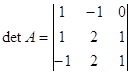
Определяем алгебраические дополнения всех элементов определителя по формуле 
; 
;
.
; 
;
.
; 
;
.
Транспонируя полученные алгебраические дополнения, получаем союзную или присоединенную матрицу Ã по отношению заданной матрицы А.
6. Вычислить определитель 3‑го порядка, разложив его по 1‑й строке
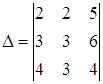
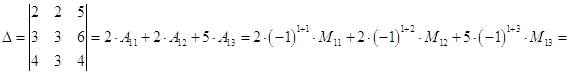
Похожие работы
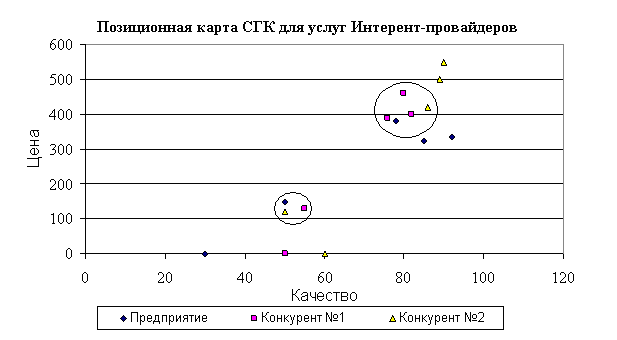
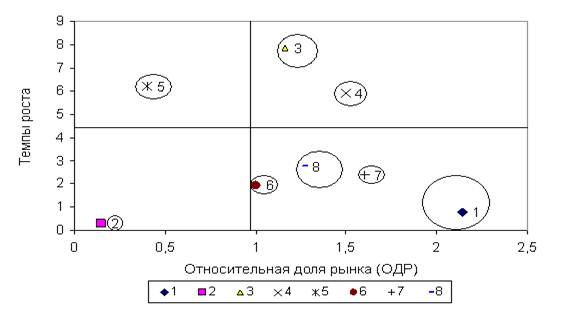
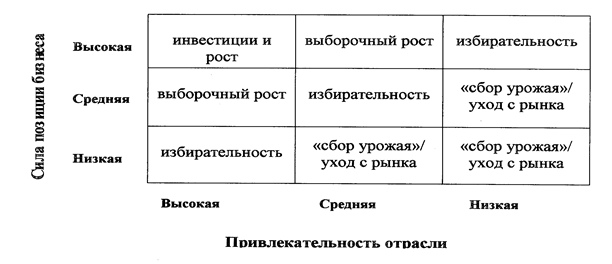
... рынка 0,78 0,29 7,84 5,9 6,19 1,96 2,4 2,75 Относительная доля рынка 2,14 0,15 1,16 1,5 0,4 1,0 1,6 1,26 Доля продукта в общем объеме реализации предприятия 37,43 1,68 25,7 2,83 8,92 2,55 2,1 20,2 Определяем центральную линию матрицы БКГ, для чего находим середину интервала максимального и минимального значений ОДР : (2,14– 0,15) : 2 = 0,99. Матрица БКГ для услуг ...
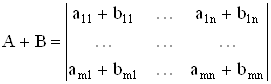
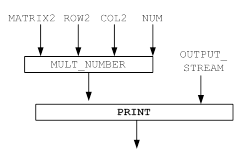
... изучения функционального анализа являются бесконечномерные векторные пространства. 1 Постановка задачи Требуется разработать программу, реализующую основные операции алгебры матриц: сложение, вычитание, умножение, транспонирование, а также умножение матрицы на число. Пример 1. Над матрицами А и В выполнить основные операции: . Сумма матриц: . Разность матриц: . Транспонирование ...
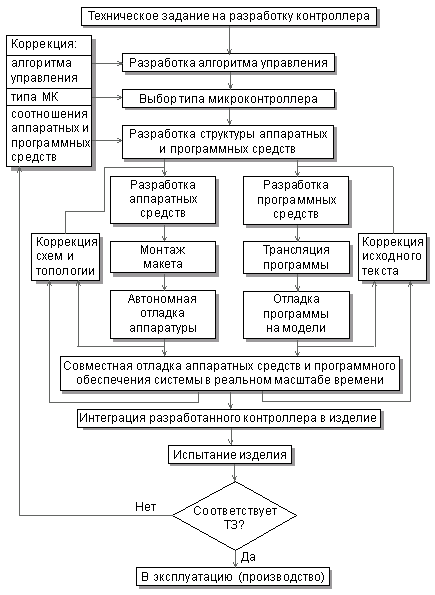
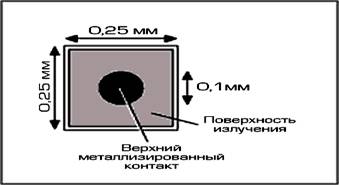
... и n-1 сегментами. Такой подход задан в светодиодном драйвере Maxim MAX6951 для управления 8-ю цифрами на всего 9-ти ножках. РАЗДЕЛ 2 РАЗРАБОТКА СВЕТОДИОДНОЙ МАТРИЦЫ 2.1 Постановка задачи Требуется разработать светодиодную матрицу, которая будет использоваться в праздничные и торжественные дни, на дискотеках, создавая различные световые эффекты. Разработка устройства будет производиться с ...
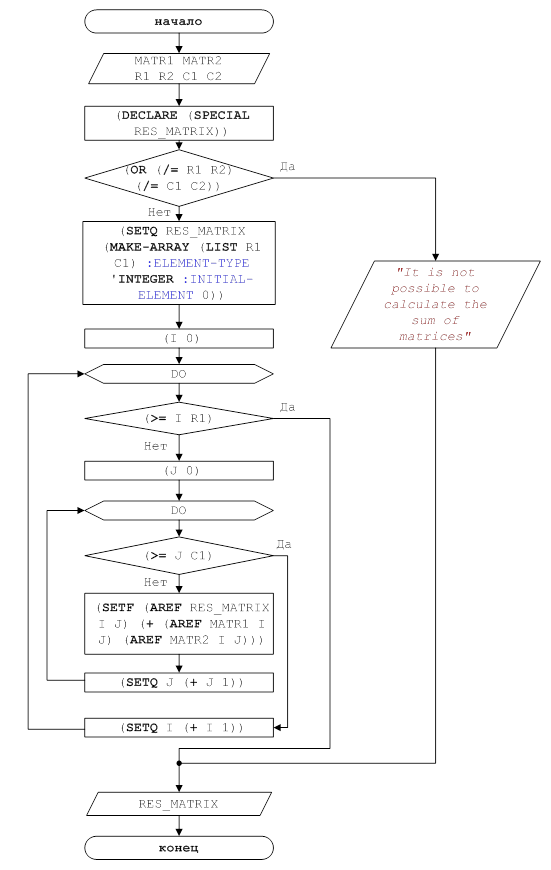
... ней примыкают задачи вычисления определителей и элементов обратной матрицы, которые иногда называют второй и третьей основными задачами линейной алгебры. В данной работе описаны методы вычисления определителя матрицы и разработана программа для его вычисления с использованием компьютера, основанная на применении метода Гаусса с выбором главного элемента. 1. ВЫБОР И ОБОСНОВАНИЕ ЧИСЛЕННОГО МЕТОДА ...
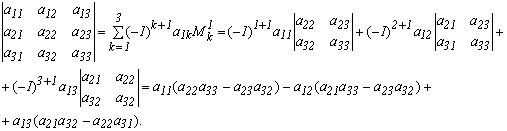
0 комментариев