Навигация
Определить алгебраические дополнения элементов 2‑й строки определителя 3-го порядка
7. Определить алгебраические дополнения элементов 2‑й строки определителя 3-го порядка
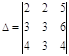
Для элемента а21 i=2, j=1 и i+j=3 число нечетное, отсюда ![]()
Для элемента а22 i=2, j=2 и i+j=4 число четное, отсюда ![]()
Для элемента а23 i=2, j=3 и i+j=5 число нечетное, отсюда ![]()
8. Найти решение системы уравнений методом Крамера
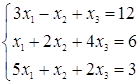
Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при X1 - n не будет равен нулю. Обозначим этот определитель знаком – Δ. Если этот определитель не равен нулю, то решаем дальше. Тогда каждый Xi = Δi / Δ, где Δi – это определитель составленный из коэффициентов при X1 - n, только значения коэффициентов в i – ом стольбце заменены на значения за знаком равенства в сисетеме уравнений, а Δ – это главный определитель
Решение
Запишем систему в виде:
Главный определить
9. Выполните операцию произведения двух матриц АхВ

Решение
Найти матрицу |C| = |A| x |B|
Вычислим элементы матрицы |C|:
c1,1 = a1,1b1,1+a1,2b2,1
c1,2 = a1,1b1,2+a1,2b2,2
c2,1 = a2,1b1,1+a2,2b2,1
c2,2 = a2,1b1,2+a2,2b2,2
| c1,1 = | 2 | * | 1 | + | 1 | * | 4 | = | 2 | + | 4 | = | 6 | |||||||||||||||||||||||||||||||||
| c1,2 = | 2 | * | -2 | + | 1 | * | 0 | = | -4 | + | 0 | = | -4 | |||||||||||||||||||||||||||||||||
| c2,1 = | -3 | * | 1 | + | 4 | * | 4 | = | -3 | + | 16 | = | 13 | |||||||||||||||||||||||||||||||||
| c2,2 = | -3 | * | -2 | + | 4 | * | 0 | = | 6 | + | 0 | = | 6 | |||||||||||||||||||||||||||||||||
Результирующая матрица |С|:
| 6 | -4 |
| 13 | 6 |
10. Какие величины называются скалярными и векторными? Приведите примеры скалярных и векторных величин? Каково условие равенства векторов? Приведите пример сложения двух векторов по правилу параллелограмма и треугольника
Скалярной величиной или просто скаляром называется величина, которая при определённом выборе единицы измерения определяется числом (удельный вес, плотность, работа, мощность, температура и т.д.)
Вектор – направленный отрезок, имеющий определённую величину (скорость, ускорение, сила, напряженность магнитного и электрического поля и т.д.).
Скалярная величина – 10 минут, векторная – 100 км/ч.
Два вектора ![]() и
и ![]() равны, если они равнонаправлены и имеют один и тот же модуль.
равны, если они равнонаправлены и имеют один и тот же модуль.
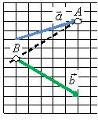
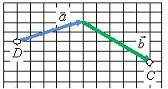
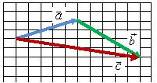
Правило треугольника
Для того чтобы сложить два вектора ![]() и
и ![]() нужно переместить вектор
нужно переместить вектор ![]() параллельно самому себе (рис. 1, б) так, чтобы его начало (точка B на рис. 1, а) совпадало с концом вектора
параллельно самому себе (рис. 1, б) так, чтобы его начало (точка B на рис. 1, а) совпадало с концом вектора ![]() (точка A на рис. 1, а). Тогда их суммой будет вектор
(точка A на рис. 1, а). Тогда их суммой будет вектор ![]() (рис. 1, г), начало которого совпадает с началом вектора
(рис. 1, г), начало которого совпадает с началом вектора ![]() (точка D на рис. 1, в), а конец – с концом вектора
(точка D на рис. 1, в), а конец – с концом вектора ![]() (точка C на рис. 1, в).
(точка C на рис. 1, в).
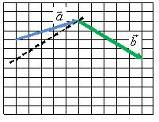
а б
в г
Рис. 1.
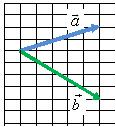
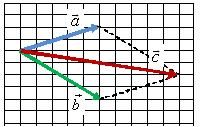
Правило параллелограмма
Для того чтобы сложить два вектора ![]() и
и ![]() нужно переместить их параллельно самим себе так, чтобы начала векторов
нужно переместить их параллельно самим себе так, чтобы начала векторов ![]() и
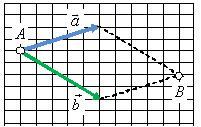
и ![]() находились в одной точке (рис. 2, а). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 2, б). Тогда их суммой будет вектор
находились в одной точке (рис. 2, а). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 2, б). Тогда их суммой будет вектор ![]() (рис. 2, в), начало которого совпадает с общим началом векторов (точка A на рис. 2, б), а конец – с противоположной вершиной параллелограмма (точка В на рис. 2, б).
(рис. 2, в), начало которого совпадает с общим началом векторов (точка A на рис. 2, б), а конец – с противоположной вершиной параллелограмма (точка В на рис. 2, б).
а
б в
Рис. 2.
11. Напишите формулу разложения вектора по трем взаимно перпендикулярным осям координат
![]()
12. Как определяется вектор через координаты его начала и конца?
Пусть известны координаты начала вектора А(x1, y1, z1) и его конца В(x2, y2, z2). Точки А и В определяют радиус вектора
|
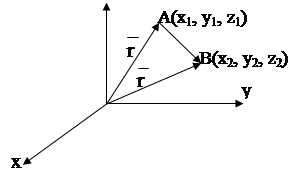
0
Рис. 3
Из треугольника ОАВ следует, что ![]() , отсюда
, отсюда ![]() .
.
Если обозначить через X, Y, Z – координаты вектора ![]() , т.е.
, т.е. ![]() =(X, Y, Z), то следует, что
=(X, Y, Z), то следует, что
X=х2-х1
Y=у2-у1
Z=z2-z1
Чтобы найти абсциссу вектора Х, необходимо из абсциссы конца вектора вычесть абсциссу начала вектора.
12. Какой вид имеет уравнение прямой в плоскости, проходящей через две точки?
![]()
13. Какой вид имеет уравнение прямой с угловым коэффициентом?
![]()
14. Напишите разложение вектора по трем взаимно перпендикулярным осям координат
| Координаты вектора | X | -2 |
| Y | 4 | |
| Z | 7 |
A (-2, 4, 7) означает, что абсцисса точки A x=-2, ордината у=4, аппликата z=7.
15. Чему равно скалярное произведение векторов ![]()
![]() и
и ![]() ? Данные для варианта взять из таблицы 2.3
? Данные для варианта взять из таблицы 2.3
| Координаты вектора | X | -2 |
| Y | 4 | |
| Z | 7 | |
| Координаты вектора | X | 3 |
| Y | 6 | |
| Z | 4 |
Т.к. векторы заданы в координатной форме, то по формуле ![]() имеем:
имеем:
![]()
16. Найти уравнение прямой, проходящей через точку пересечения прямых l1 и l2 и отсекающей на оси абсцисс отрезок, равный d
| Уравнение прямой l1 | Уравнение прямой l2 | d | Координаты точки Р | |
| x | y | |||
| 3x‑2y‑7=0 | x+3y‑6=0 | 3 | 2 | 5 |
![]()
Отсюда находим х = 6 – 3у

x = 3
Значит точка пересечения двух прямых A (3; 1)
По условия отрезок равен 3, значит координата точки B (3; 0).
Найдем уравнение прямой, проходящей через точки А и В.
![]()
![]()
Здесь знаменатель равен нулю. Полагаем числитель левой части равным нулю.
Получаем ![]()
17. Найти уравнение прямой, отсекающей на оси ординат отрезок, равный d и проходящей параллельно прямой l1
| Уравнение прямой l1 | Уравнение прямой l2 | d | Координаты точки Р | |
| x | y | |||
| 3x‑2y‑7=0 | x+3y‑6=0 | 3 | 2 | 5 |
Найдем две точки прямой 3x‑2y‑7=0
Подставим в уравнение х=1 и х=3 и получим значения у соответственно -2 и 1.
A (1; – 2) и B (3; 1).
Координаты направляющего вектора ![]() найдём по координатам конца и начала вектора
найдём по координатам конца и начала вектора ![]()
![]()
![]()
Подставляя в формулу ![]() координаты точки O (0; 3) и координаты вектора
координаты точки O (0; 3) и координаты вектора ![]() получим искомое уравнение прямой
получим искомое уравнение прямой
![]() или
или ![]() .
.
18. Как определяются горизонтальные асимптоты функции?
В случае если наклонная асимптота расположена горизонтально, то есть при ![]() , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота – частный случай наклонной асимптоты; прямая y = с = const является горизонтальной асимптотой графика y = f(x) при
, она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота – частный случай наклонной асимптоты; прямая y = с = const является горизонтальной асимптотой графика y = f(x) при ![]() или
или ![]() , если
, если
![]()
или
![]()
соответственно.
19. Что такое частное приращение функции нескольких переменных?
Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных ![]() в точке
в точке ![]() частные производные определяются так:
частные производные определяются так:
![]() ,
,
![]() ,
,
если эти пределы существуют.
Из определения следует геометрический смысл частной производной функции двух переменных: частная производная ![]() – угловой коэффициент касательной к линии пересечения поверхности
– угловой коэффициент касательной к линии пересечения поверхности ![]() и плоскости
и плоскости ![]()
![]() в соответствующей точке.
в соответствующей точке.
20. Каковы выражения для частных дифференциалов функции z=f (x, y)?
Частной производной по x функции z = f (x, y) в точке M0(x0, y0) называется предел ![]() ,
,
если этот предел существует. Обозначается эта частная производная любым из следующих символов:
![]() ;
;![]() ;
;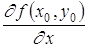 .
.
Частная производная по x есть обычная производная от функции z = f (x, y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.
Совершенно аналогично можно определить частную производную по y функции z = f (x, y) в точке M0(x0, y0):
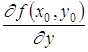 =
=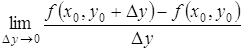 .
.
Приведем примеры вычисления частных производных
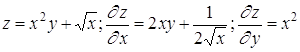

21. Каково выражение для полного дифференциала функции u=u (x, y, z)?
Полный дифференциал du функции u = f (x, y, z) (если он существует) равен сумме всех ее частных дифференциалов:
![]()
22. Напишите частные производные третьего порядка для функции z=f (x, y, z)
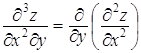
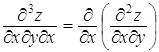
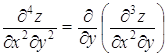
23. Найти частную производную и частный дифференциал функции. 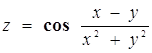
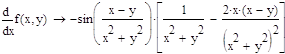

24. Вычислить значения частных производных f’x(M0), f’y(M0), f’z(M0) для данной функции f (x, y, z) в точке M0(x0, y0, z0) с точностью до двух знаков после запятой
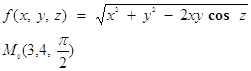
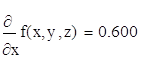
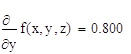
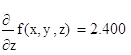
25. Вычислить значения частных производных функции z (x, y), заданной неявно, в данной точке M0(x0, y0, z0) с точностью до двух знаков после запятой
lnZ=x+2y-z+ln3 M0(1,1,3)
![]()
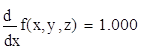
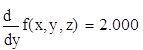
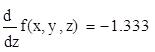
26. Найти уравнение касательной плоскости и нормали к заданной поверхности S в точке M0(x0, y0, z0). S: z=x2+y2-4xy+3x‑15, M0(-1,3,4)
![]()
![]()
![]()
![]()
Следовательно, уравнение касательной плоскости будет таким:
![]()
![]()
а уравнение нормали таким:
![]()
Похожие работы
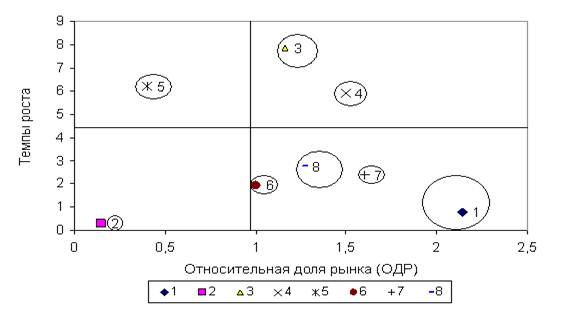
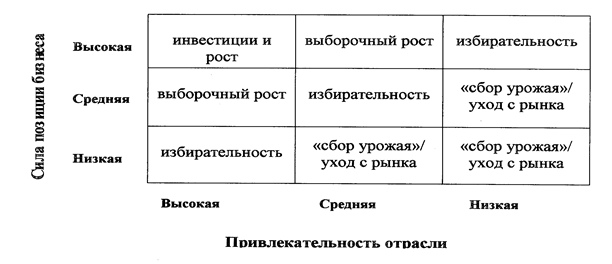
... рынка 0,78 0,29 7,84 5,9 6,19 1,96 2,4 2,75 Относительная доля рынка 2,14 0,15 1,16 1,5 0,4 1,0 1,6 1,26 Доля продукта в общем объеме реализации предприятия 37,43 1,68 25,7 2,83 8,92 2,55 2,1 20,2 Определяем центральную линию матрицы БКГ, для чего находим середину интервала максимального и минимального значений ОДР : (2,14– 0,15) : 2 = 0,99. Матрица БКГ для услуг ...
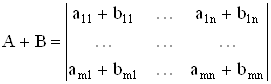
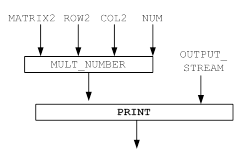
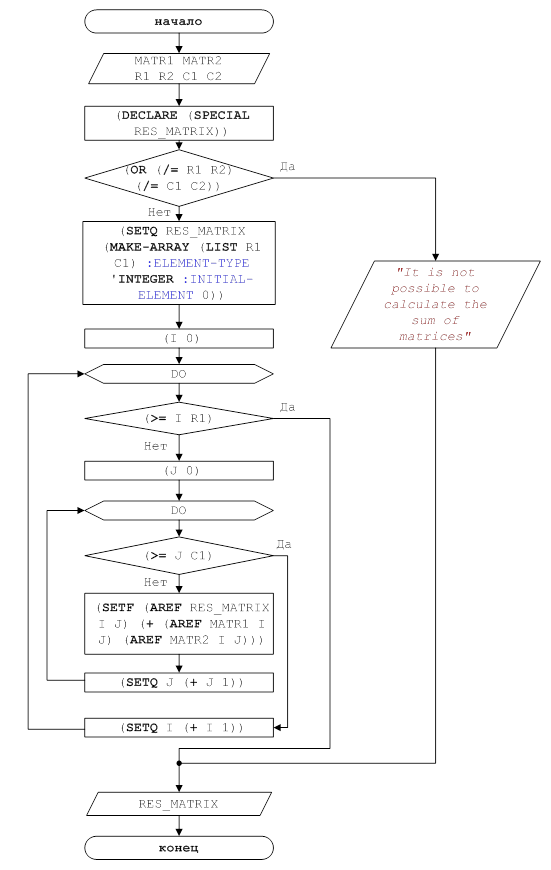
... изучения функционального анализа являются бесконечномерные векторные пространства. 1 Постановка задачи Требуется разработать программу, реализующую основные операции алгебры матриц: сложение, вычитание, умножение, транспонирование, а также умножение матрицы на число. Пример 1. Над матрицами А и В выполнить основные операции: . Сумма матриц: . Разность матриц: . Транспонирование ...
... и n-1 сегментами. Такой подход задан в светодиодном драйвере Maxim MAX6951 для управления 8-ю цифрами на всего 9-ти ножках. РАЗДЕЛ 2 РАЗРАБОТКА СВЕТОДИОДНОЙ МАТРИЦЫ 2.1 Постановка задачи Требуется разработать светодиодную матрицу, которая будет использоваться в праздничные и торжественные дни, на дискотеках, создавая различные световые эффекты. Разработка устройства будет производиться с ...
... ней примыкают задачи вычисления определителей и элементов обратной матрицы, которые иногда называют второй и третьей основными задачами линейной алгебры. В данной работе описаны методы вычисления определителя матрицы и разработана программа для его вычисления с использованием компьютера, основанная на применении метода Гаусса с выбором главного элемента. 1. ВЫБОР И ОБОСНОВАНИЕ ЧИСЛЕННОГО МЕТОДА ...


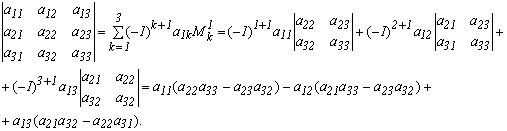

0 комментариев