Навигация
Статистическая обработка результатов и их сравнение с результатами аналитического моделирования
30846
знаков
2
таблицы
11
изображений
3.4 Статистическая обработка результатов и их сравнение с результатами аналитического моделирования
Т.к. показатели эффективности получаются в результате моделирования СМО в течение конечного времени, они содержат случайную компоненту. Поэтому, для получения более надежных результатов нужно провести их статистическую обработку. С этой целью оценим доверительный интервал для них по результатам 20 прогонов программы.
Величина 
попадает в доверительный интервал, если выполняется неравенство
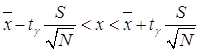, где
математическое ожидание (среднее значение), находится по формуле
,
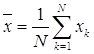исправленная дисперсия,
,
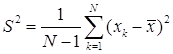N=20 – число прогонов,
– надежность. При 
и N=20 
.
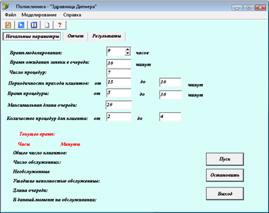
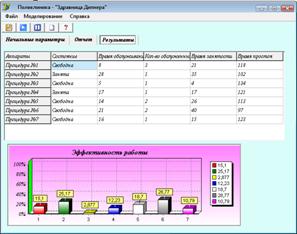
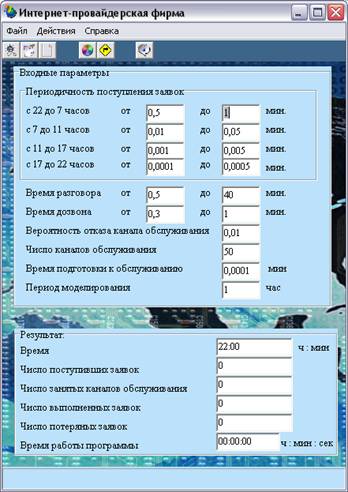
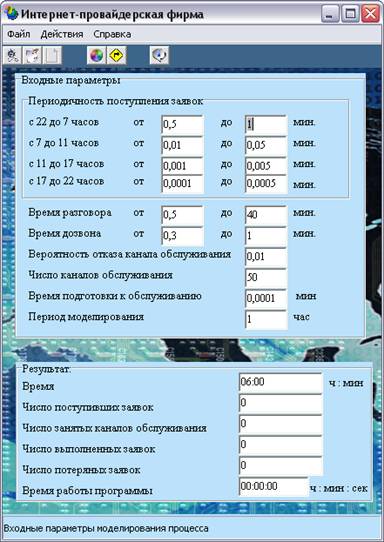
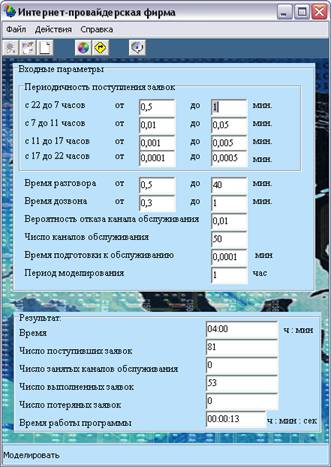
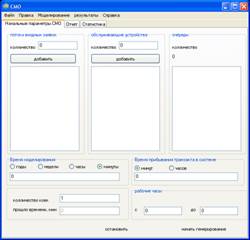
Результат работы программы представлен на рис. 6.
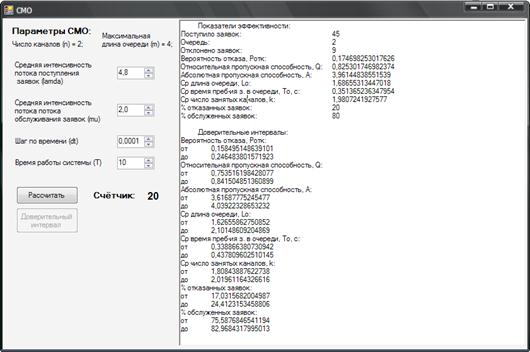
Рис. 6. Вид программы
Для удобства сравнения результатов, полученных различными методами моделирования, представим их в виде таблицы.
Таблица 2.
| Показатели эффективности СМО | Результаты аналитического моделирования | Результаты имитационного моделирования (послед. шаг) | Результаты имитационного моделирования | |
| Нижняя граница доверительного интервала | Верхняя граница доверительного интервала | |||
| Вероятность отказа |
| 0,174698253017626 | 0,158495148639101 | 0,246483801571923 |
| Относительная пропускная способность |
| 0,825301746982374 | 0,753516198428077 | 0,841504851360899 |
| Абсолютная пропускная способность |
| 3,96144838551539 | 3,61687775245477 | 4,03922328653232 |
| Средняя длина очереди |
| 1,68655313447018 | 1,62655862750852 | 2,10148609204869 |
| Среднее время пребывания заявки в очереди | 0,4242558575 | 0,351365236347954 | 0,338866380730942 | 0,437809602510145 |
| Среднее число занятых каналов |
| 1,9807241927577 | 1,80843887622738 | 2,01961164326616 |
Из табл. 2 видно, что результаты, полученные при аналитическом моделировании СМО, попадают в доверительный интервал, полученный по результатам имитационного моделирования. Т.е., результаты, полученные разными методами, согласуются.
Заключение
В данной работе рассмотрены основные методы моделирования СМО и расчета показателей их эффективности.
Проведено моделирование двухканальной СМО с максимальной длиной очереди равной 4 с помощью уравнений Колмогорова, а также, найдены финальные вероятности состояний системы. Рассчитаны показатели ее эффективности.
Проведено имитационное моделирование работы такой СМО. На языке программирования C# составлена программа, имитирующая ее работу. Проведена серия расчетов, по результатам которых найдены значения показателей эффективности системы и выполнена их статистическая обработка.
Полученные при имитационном моделировании результаты согласуются с результатами аналитического моделирования.
Литература
1. Вентцель Е.С. Исследование операций. – М.: Дрофа, 2004. – 208 с.
2. Волков И.К., Загоруйко Е.А. Исследование операций. – М.: Изд.-во МГТУ им. Н.Э. Баумана, 2002. – 435 с.
3. Волков И.К., Зуев С.М., Цветкова Г.М. Случайные процессы. – М.: Изд.-во МГТУ им. Н.Э. Баумана, 2000. – 447 с.
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979. – 400 с.
5. Ивницкий В.Л. Теория сетей массового обслуживания. – М.: Физматлит, 2004. – 772 с.
6. Исследование операций в экономике/ под ред. Н.Ш. Кремера. – М.: Юнити, 2004. – 407 с.
7. Таха Х.А. Введение в исследование операций. – М.: ИД «Вильямс», 2005. – 902 с.
8. Харин Ю.С., Малюгин В.И., Кирлица В.П. и др. Основы имитационного и статистического моделирования. – Минск: Дизайн ПРО, 1997. – 288 с.
Похожие работы
... очередь длины k, остается в ней с вероятностью Pk и не присоединяется к очереди с вероятностью gk=1 - Pk,'. именно так обычно ведут себя люди в очередях. В системах массового обслуживания, являющихся математическими моделями производственных процессов, возможная длина очереди ограничена постоянной величиной (емкость бункера, например). Очевидно, это частный случай общей постановки. Некоторые ...
... (с 17 до 22 часов)время суток. Следовательно при одном и том же количестве каналов обслуживания, в ночное время вероятность занятости канала будет меньше, чем в дневное. Особенностью этой модели системы массового обслуживания является отсутствие очереди. Если в момент совершения заявки свободных каналов не оказалось, то она покидает систему: то есть если клиент не дозванивается, то и факт ...
... лабораторной работе, входит: 1. Анализ зависимости влияния экзогенных переменных модели однофазной одноканальной СМО на эндогенные переменные. 2. Построение плана машинного эксперимента на основе множественного регрессионного анализа и метода наименьших квадратов. 3.Моделирование системы массового обслуживания В качестве объекта моделирования рассматривается однофазная одноканальная система, ...
... каналов обслуживан6ия, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что заявка будет обслужена; математического ожидания числа обслуженных заявок и т.д.) от входных ...
0 комментариев