Навигация
Исследование функций и построение их графиков
Тема 1. Предел функции
Число А называется пределом функции ![]() при
при ![]() , стремящимся к
, стремящимся к ![]() , если для любого положительного числа
, если для любого положительного числа ![]() (
(![]() >0) найдется такое положительное число
>0) найдется такое положительное число ![]() >0 (зависящее в общем случае от
>0 (зависящее в общем случае от ![]() ), что для всех
), что для всех ![]() , не равных
, не равных ![]() и удовлетворяющих условию x
и удовлетворяющих условию x![]() x<
x<![]() , выполняется неравенство x
, выполняется неравенство x![]() А x<
А x<![]() .
.
Для предела функции вводится обозначение ![]()
![]() =А.
=А.
Пределы функций обладают следующими основными свойствами:
Функция не может иметь более одного предела.
Если ![]() = С (постоянная), то
= С (постоянная), то ![]() С.
С.
Если существует ![]() А, то для любого числа
А, то для любого числа ![]() верно:
верно:
![]()
Если существуют ![]() А и
А и ![]() В, то
В, то ![]() =
= ![]() АВ,
АВ, ![]() а если В
а если В![]() 0, то
0, то
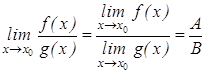 .
.
Операция предельного перехода перестановочна с операцией вычисления непрерывной функции, т. е. справедлива формула ![]()
Если функция ![]() непрерывна в точке
непрерывна в точке ![]() , то искомый предел равен значению функции в этой точке, т.е. он находится непосредственной подстановкой предельного значения переменной вместо аргумента
, то искомый предел равен значению функции в этой точке, т.е. он находится непосредственной подстановкой предельного значения переменной вместо аргумента ![]() :
: ![]()
Функция ![]() (
(![]() называется бесконечно малой величиной при
называется бесконечно малой величиной при ![]() , если ее предел равен нулю:
, если ее предел равен нулю: ![]() Функция
Функция ![]() называется бесконечно большой величиной при
называется бесконечно большой величиной при ![]() , если
, если ![]()
Пример 1. ![]()
![]()
![]() 9.
9.
Пример 2. ![]()
![]()
![]()
![]() .
.
В рассмотренных примерах предел находился сразу: в виде числа или символа ![]() (бесконечность). Но чаще при вычислении пределов мы встречаемся с неопределенностями, когда результат нахождения предела не ясен, например, в случае отношения двух бесконечно малых функций (условное обозначение
(бесконечность). Но чаще при вычислении пределов мы встречаемся с неопределенностями, когда результат нахождения предела не ясен, например, в случае отношения двух бесконечно малых функций (условное обозначение ![]() ) или бесконечно больших (
) или бесконечно больших (![]() ).Кроме названных встречаются неопределенности вида
).Кроме названных встречаются неопределенности вида ![]()
Для раскрытия неопределенностей используются специальные приемы и два следующих предела, которые играют особую роль в математике и поэтому называются замечательными:
- первый замечательный предел ![]()
-второй замечательный предел ![]() (число Эйлера).
(число Эйлера).
Пример 3. ![]() .
.
Решение. Непосредственной подстановкой убеждаемся, что имеем дело с неопределенностью вида ![]() :
:
![]() .
.
Для раскрытия неопределенности разложим числитель и знаменатель на множители. Найдем корни многочлена, стоящего в числителе. Для этого составим уравнение второй степени ![]() и найдем его решение:
и найдем его решение:
![]()
![]()
Тогда для квадратного трехчлена справедливо разложение на множители
![]() .
.
Аналогичные действия выполним для многочлена, стоящего в знаменателе.
Уравнение ![]() имеет решения
имеет решения
![]()
![]()
и знаменатель представляется в виде:![]()
Сократим дробь на множитель ![]() и вычислим ее при
и вычислим ее при ![]()
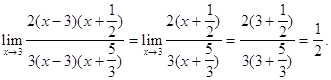
Пример 4. ![]()
Решение. Непосредственной подстановкой убеждаемся, что возникает неопределенность вида ![]() . Для раскрытия неопределенности умножим числитель и знаменатель на выражение
. Для раскрытия неопределенности умножим числитель и знаменатель на выражение ![]() , являющееся сопряженным к знаменателю
, являющееся сопряженным к знаменателю
![]()
= ![]() .
.
Пример 5. ![]() .
.
Решение. Имеем неопределенность вида ![]() . Разделим числитель и знаменатель на
. Разделим числитель и знаменатель на ![]() (в более общем случае, когда числитель и знаменатель представляют многочлены разных степеней, делят на
(в более общем случае, когда числитель и знаменатель представляют многочлены разных степеней, делят на ![]() с наибольшим показателем степени числителя и знаменателя). Используя свойства пределов, получим:
с наибольшим показателем степени числителя и знаменателя). Используя свойства пределов, получим:
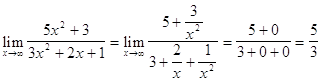 .
.
Пример 6. ![]() .
.
Решение. При ![]() имеем неопределенность вида
имеем неопределенность вида ![]() . Представим
. Представим ![]() , разделим и умножим числитель и знаменатель на числа 2, 5 и
, разделим и умножим числитель и знаменатель на числа 2, 5 и ![]() , тогда предел преобразуется к виду:
, тогда предел преобразуется к виду:
![]()
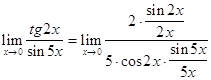 .
.
Пользуясь свойствами пределов и первым замечательным пределом, далее имеем:
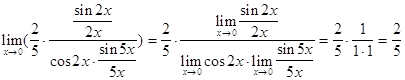 .
.
Пример 7. ![]() .
.
Решение. Имеем неопределенность вида [![]() ], так как
], так как
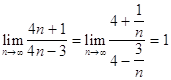 , а
, а ![]() .
.
Выделим у дроби целую часть
![]() .
.
Введем новую переменную ![]() и выразим отсюда
и выразим отсюда ![]() через
через ![]() :
: ![]() . Тогда
. Тогда
![]()
Заметим, что при ![]() переменная
переменная ![]() . Теперь, переходя к новой переменной и используя второй замечательный предел, получим:
. Теперь, переходя к новой переменной и используя второй замечательный предел, получим:
![]()
=![]() .
.
Неопределенности вида ![]() путем алгебраических преобразований приводятся к виду
путем алгебраических преобразований приводятся к виду ![]() . Неопределенности вида
. Неопределенности вида ![]() ,
, ![]() можно раскрыть, предварительно прологарифмировав соответствующую функцию. Неопределенности вида
можно раскрыть, предварительно прологарифмировав соответствующую функцию. Неопределенности вида ![]() можно исключить, используя правило Лопиталя, которое изложено в конце темы 2.
можно исключить, используя правило Лопиталя, которое изложено в конце темы 2.
Пример 8. Первоначальный вклад в банк составил ![]() денежных единиц. Банк выплачивает ежегодно
денежных единиц. Банк выплачивает ежегодно ![]() % годовых. Необходимо найти размер вклада
% годовых. Необходимо найти размер вклада ![]() через
через ![]() лет при непрерывном начислении процентов. Решить задачу при
лет при непрерывном начислении процентов. Решить задачу при ![]() =10,
=10, ![]() =5%,
=5%, ![]() =20 лет.
=20 лет.
Решение. При ![]() % годовых размер вклада ежегодно будет увеличиваться в
% годовых размер вклада ежегодно будет увеличиваться в
![]() раз, т.е.
раз, т.е. ![]() .
.
Если начислять проценты по вкладам не один раз в год, а ![]() раз, то размер вклада за
раз, то размер вклада за ![]() лет при
лет при ![]() начислениях составит
начислениях составит
![]() .
.
Тогда размер вклада за ![]() лет при непрерывном начислении процентов (
лет при непрерывном начислении процентов (![]() ) сводится к нахождению предела
) сводится к нахождению предела
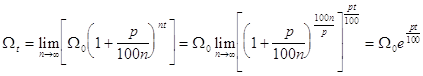 .
.
Здесь при решении использовался второй замечательный предел.
Подставляя исходные числовые данные задачи, получаем
![]() (ден. единиц).
(ден. единиц).
Вопросы для самопроверки
Дайте определение предела функции в точке.
Назовите основные свойства пределов функций.
Какие виды неопределенностей встречаются при нахождении пределов?
Какие пределы называются замечательными?
Какие функции называют бесконечно малыми?
Задачи для самостоятельной работы
Найти пределы следующих функций:
| Номер варианта | А) | Б) |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
Таблица 1.
Тема 2. Производная функции
Приращением функции ![]() в точке
в точке ![]() , соответствующим приращению аргумента
, соответствующим приращению аргумента ![]() , называется число
, называется число ![]() .
.
Производной функции ![]() в точке
в точке ![]() называется предел отношения приращения функции
называется предел отношения приращения функции ![]() к приращению аргумента
к приращению аргумента ![]() при
при ![]() , если этот предел существует, и обозначается:
, если этот предел существует, и обозначается:
![]() .
.
Нахождение производной функции называется дифференцированием этой функции. Если функция ![]() имеет в точке
имеет в точке ![]() конечную производную, то функция называется дифференцируемой в этой точке.
конечную производную, то функция называется дифференцируемой в этой точке.
Важнейшими правилами дифференцирования являются следующие.
Производная постоянной ![]() равна нулю:
равна нулю: ![]() .
.
Постоянный множитель выносится за знак производной
![]() .
.
Производная суммы (разности) функций равна сумме (разности) производных этих функций
![]() .
.
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго
![]() .
.
Производная частного двух дифференцируемых функций находится по формуле
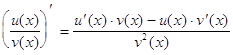 .
.
Пусть переменная ![]() есть функция от переменной
есть функция от переменной ![]() (например,
(например, ![]() ), а переменная
), а переменная ![]() , в свою очередь, есть функция от независимой переменной
, в свою очередь, есть функция от независимой переменной ![]() (
(![]() ), иначе задана сложная функция
), иначе задана сложная функция ![]() .
.
Если ![]() и
и ![]() - дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу
- дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу ![]() , умноженной на производную самого промежуточного аргумента по независимой переменной
, умноженной на производную самого промежуточного аргумента по независимой переменной ![]() :
:
![]()
Если функция, производную которой нужно найти, представляет из себя комбинацию элементарных функций, то для вычисления производной применяются правила дифференцирования и таблица производных элементарных функций, приводимая ниже.
Таблица 2.
| № | функция | производная | № | функция | производная |
| 1 | | | 7 | | 1/ |
| 2 | | | 8 | | -1/ |
| 3 | | 1/ | 9 | | 1/( |
| 4 | | | 10 | | -1/( |
| 5 | | | 11 | | 1/(1+ |
| 6 | | - | 12 | | -1/(1+ |
Пример 1. Найти производную функции
![]() .
.
Решение. Представим ее как сложную функцию. Пусть ![]() , тогда
, тогда ![]() и
и ![]() . Найдем производную по промежуточному аргументу
. Найдем производную по промежуточному аргументу ![]() как степенной функции
как степенной функции
![]() .
.
В свою очередь, промежуточный аргумент ![]() представляется в виде суммы двух степенных функций минус постоянная, поэтому, используя правила 1-3,по-лучим
представляется в виде суммы двух степенных функций минус постоянная, поэтому, используя правила 1-3,по-лучим
![]()
=![]() .
.
Отсюда производная искомой функции
![]() .
.
Пример 2. Найти производную функции
![]() .
.
Решение. Обозначим![]() ,
, ![]() . Тогда
. Тогда ![]()
![]() и искомая производная находится из формулы
и искомая производная находится из формулы ![]() .
.
Производную ![]() находим из таблицы производных элементарных функций
находим из таблицы производных элементарных функций
![]() .
.
Второй сомножитель ![]() представляет производную от степенной функции
представляет производную от степенной функции
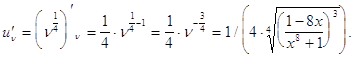
Наконец, последняя производная ![]() находится по правилам дифференцирования частного
находится по правилам дифференцирования частного
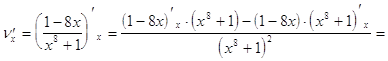
=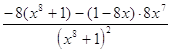 =
=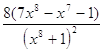 .
.
В итоге получаем искомую производную
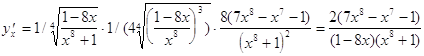 .
.
Пример 3. Наити производную
![]() .
.
Решение. Производная суммы двух функций есть сумма их производных
![]() .
.
Для нахождения производной первого слагаемого ![]() обозначим
обозначим ![]() ,
, ![]() .
.
Тогда ![]() ,
,
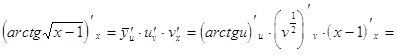
=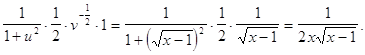
Производную второго слагаемого ![]() найдем по правилу дифференцирования степенно-показательной функции. Прологарифмируем функцию
найдем по правилу дифференцирования степенно-показательной функции. Прологарифмируем функцию ![]() :
: ![]() Дифференцируем левую и правую часть полученного равенства
Дифференцируем левую и правую часть полученного равенства
![]()
Отсюда
![]()
Наконец, находим производную искомой функции
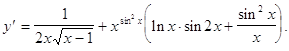
Пример 4. На основе опытных данных построена математическая модель спроса ![]() населения на некоторый товар в зависимости от цены
населения на некоторый товар в зависимости от цены ![]() :
:
![]() .
.
Определить эластичность спроса при ![]() (в условных денежных един.).
(в условных денежных един.).
Решение. Эластичностью спроса ![]() называют предел отношения относительного приращения спроса
называют предел отношения относительного приращения спроса ![]() к относительному приращению цены
к относительному приращению цены ![]() при
при ![]() :
:
![]() .
.
Если ![]() >1, то спрос называют эластичным, при
>1, то спрос называют эластичным, при ![]() <1 – неэластичным, а при
<1 – неэластичным, а при ![]() нейтральным.
нейтральным.
Найдем производную
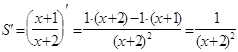 .
.
Тогда
![]() .
.
Определим эластичность спроса при ![]() :
:![]() . Таким образом, при такой цене имеем неэластичный спрос.
. Таким образом, при такой цене имеем неэластичный спрос.
Правило Лопиталя. При нахождении пределов функций (тема 1) неопределенности вида ![]() можно исключить, применяя правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, т. е.
можно исключить, применяя правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если последний существует, т. е.
![]()
Если ![]() (или
(или ![]() ), то правило Лопиталя можно использовать вторично, т.е.
), то правило Лопиталя можно использовать вторично, т.е.
![]()
В общем случае правило Лопиталя можно применять неоднократно.
Пример 5. Найти
![]()
Решение. Для раскрытия неопределенности применим правило Лопиталя.
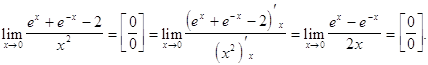
Неопределенность вида ![]() по-прежнему сохраняется. Применим правило Лопиталя еще раз:
по-прежнему сохраняется. Применим правило Лопиталя еще раз:
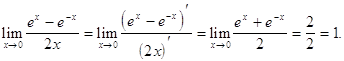
Вопросы для самопроверки
Дайте определение производной функции в точке.
Какая функция называется дифференцируемой в точке?
Назовите важнейшие правила дифференцирования.
Как находится производная сложной функции?
Сформулируйте правило Лопиталя.
Задачи для самостоятельной работы
Найти производные следующих функций:
Таблица 3.
| Номер варианта | А) | Б) | В) |
| 1 | y=(3x4-4x(-1/4)+2)5 | y=arccos2x+(1-4x2)1/2 | y=2tgx+x sin(2x |
| 2 | y=(5x2+4x(5/4)+3)3 | y=arctg(x2-1)1/2 | y=e3x-2x tg(3x) |
| 3 | y=(0.25x8+8x(3/8)-1)3 | y=arccos(1-x2)1/2 | y=3cosx-x sin(2x) |
| 4 | y=(0.2x5-3x(4/3)-4)4 | y=arctg(x-1)1/2 |
|
| 5 | y=(3x8+5x(2/5)-3)5 | y=arctg(2/(x-3)) |
|
| 6 | y=(5x4-2x(-3/2)+3)4 | y=arccos(1-x)1/2 |
|
| 7 | y=(4x3+3x(-4/3)-2)5 | y=arcctg(x-1)1/2 |
|
| 8 | y=(7x5-3x(5/3)-6)4 | y=arcsin3x-(1-9x2)1/2 | y=etgx-x1/2 cos(2x). |
| 9 | y=(3x4-4x(-1/4)-3)5 | y=arctg(1/(x-1)) | y=x tg3x+2x-2 |
| 10 | y=(8x3-9x(-7/3)+6)5 | y=arcsin((1-x)1/2) |
|
Тема 3. Применение дифференциала функции в приближенных вычислениях
Дифференциалом функции ![]() в точке
в точке ![]() называется главная, линейная относительно приращения аргумента
называется главная, линейная относительно приращения аргумента ![]() часть приращения функции
часть приращения функции ![]() , равная произведению производной функции в точке
, равная произведению производной функции в точке ![]() на приращение независимой переменной:
на приращение независимой переменной:
![]() .
.
Отсюда приращение функции ![]() отличается от ее дифференциала
отличается от ее дифференциала ![]() на бесконечно малую величину и при достаточно малых значениях можно считать
на бесконечно малую величину и при достаточно малых значениях можно считать ![]() или
или
![]() .
.
Приведенная формула используется в приближенных вычислениях.
Пример. Вычислить приближенно ![]()
Решение. Рассмотрим функцию ![]() . Это степенная функция и ее производная найдется:
. Это степенная функция и ее производная найдется:
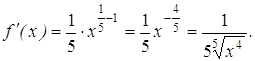
В качестве ![]() требуется взять число, удовлетворяющее условиям:
требуется взять число, удовлетворяющее условиям:
- значение ![]() известно или достаточно просто вычисляется;
известно или достаточно просто вычисляется;
- число ![]() должно быть близким к числу 33,2, т.е. приращение
должно быть близким к числу 33,2, т.е. приращение ![]() должно быть как можно меньше.
должно быть как можно меньше.
В нашем случае этим требованиям удовлетворяет число ![]() = 32, для которого
= 32, для которого ![]() = 2,
= 2, ![]() = 33,2 -32 = 1,2.
= 33,2 -32 = 1,2.
Применяя формулу, находим искомое число:
![]()
![]() +
+ 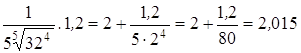 .
.
Вопросы для самопроверки
Похожие работы
... пунктах были рассмотрены методы исследования поведения функции с помощью производной. Однако среди вопросов, касающихся полного исследования функции, есть и такие, которые с производной не связаны. Так, например, необходимо знать, как ведет себя функция при бесконечном удалении точки ее графика от начала координат. Такая проблема может возникнуть в двух случаях: когда аргумент функции уходит на ...
... работа как прием обучения может входить почти во все методы обучения, воспитывать в учениках потребность самостоятельно добывать знания, умение творчески пользоваться объяснениями учителя, помощью товарищей, книгами, конспектами одна из важнейших целей нашей работы.ГЛАВА 2. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИЙ ПРИЁМЫ И МЕТОДЫ §1. Анализ программ и учебников «Алгебра, 7», «Алгебра, ...
... функций обычно сводится к исследованию однозначных. Переменная величина у есть функция аргумента х, т.е. y=f(x), если каждому возможному значению х соответствует одно определённое значение у. Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f(x). Горизонтальную ось Ох называют осью абсцисс, вертикальную ось Оу - ...
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
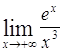
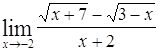
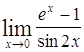
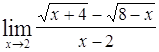
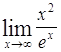
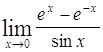
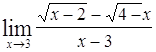
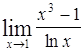
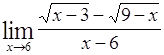
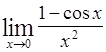
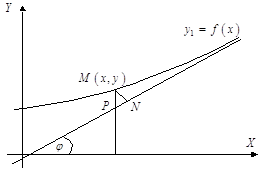

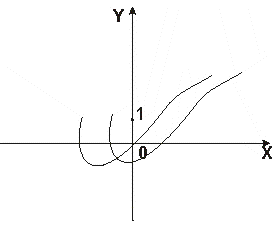
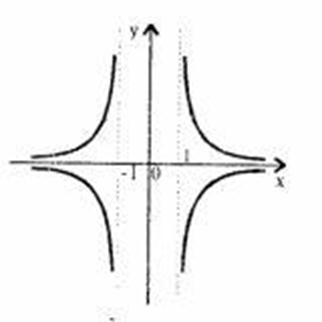
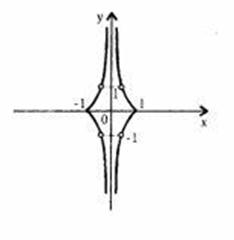
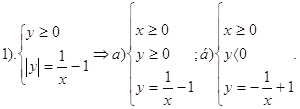
0 комментариев