Введение
Данная курсовая работа включает в себя три итерационных метода решения систем линейных алгебраических уравнений (СЛАУ):
1. Метод Якоби (метод итераций).
2. Метод Холецкого.
3. Метод верхней релаксации.
Также данная курсовая работа включает в себя: описание метода, применение метода к конкретной задаче (анализ), код программы решения вышеперечисленных методов на языке программирования Borland C++ Builder 6.
Описание метода
Метод решения задачи называют итерационным, если в результате получают бесконечную последовательность приближений к решению. Основное достоинство итерационных методов состоит в том, что точность искомого решения задается. Число итераций, которое необходимо выполнить для получения заданной точности ![]() , является основной оценкой качества метода. По этому числу проводится сравнение различных методов.
, является основной оценкой качества метода. По этому числу проводится сравнение различных методов.
Главным недостатком этих методов является то, что вопрос сходимости итерационного процесса требует отдельного исследования. Примером обычных итерационных методов служат: метод итераций (метод Якоби), метод Зейделя, метод верхних релаксаций.
Начнем с метода итераций или как его ещё называют метода Якоби.
Существует сиcтема A·x = f (1), где матрица A = [aij] (i, j = 1, 2, …m) имеет обратную матрицу; x = (x1, x2, x3,… xm) – вектор неизвестных, f – вектор свободных членов. Систему (1) нужно преобразовать к следующему виду: ![]() (2) i=1, 2,…, m, где
(2) i=1, 2,…, m, где ![]() ,
, ![]() , при этом aii
, при этом aii ![]() 0.
0.
Значение суммы считается равным 0, если верхний предел суммирования меньше нижнего. Тогда при i=1 уравнение имеет вид: ![]() (3). В методе Якоби исходят из записи системы в виде (2), итерации при этом определяют следующим образом:
(3). В методе Якоби исходят из записи системы в виде (2), итерации при этом определяют следующим образом: ![]() , (n=0, 1, …, n0, i=1, 2, …, m) (4).
, (n=0, 1, …, n0, i=1, 2, …, m) (4).
Начальные значения ![]() – (i=0, 1, …, m) задаются произвольно (в программе мы это проделываем, вводя функцию по генерации случайных чисел – «random»). Окончание итерационного процесса определяют либо заданием максимального числа итераций n0, либо следующим условием:
– (i=0, 1, …, m) задаются произвольно (в программе мы это проделываем, вводя функцию по генерации случайных чисел – «random»). Окончание итерационного процесса определяют либо заданием максимального числа итераций n0, либо следующим условием: ![]() , где
, где ![]() >0. В качестве нулевого приближения в системе (4) примем
>0. В качестве нулевого приближения в системе (4) примем ![]() .
.
Если последовательность приближений x1(0), x2(0),…, xm(0), x1(1), x2(1),…, xm(1),…, x1(k), x2(k),…, xm(k) имеет предел ![]() ,
, ![]() , то этот предел является решением системы (2).
, то этот предел является решением системы (2).
Достаточным условием сходимости решения системы (1) является то, что матрица A является матрицей с преобладающими диагональными элементами, то есть ![]() , i=1, 2, …, m.
, i=1, 2, …, m.
Теперь рассмотрим второй итерационный метод – метод Зейделя, который является модификацией метода Якоби. Основная его идея заключается в том, что при вычислении (k+1) – го приближения неизвестной xi учитываются уже вычисленные ранее (k+1) – е приближения (x1 x2,…, xi-1).
Пусть дана приведенная линейная система: ![]() (i = 1, 2, …n) (5). Выбираются произвольно начальные приближения корней x1(0), x2(0),…, xn(0), чтобы они в какой-то мере соответствовали неизвестным x1, x2, x3,…, xn.
(i = 1, 2, …n) (5). Выбираются произвольно начальные приближения корней x1(0), x2(0),…, xn(0), чтобы они в какой-то мере соответствовали неизвестным x1, x2, x3,…, xn.
Предполагается, что k-е приближение ![]() корней известно, тогда в соответствии с идеей метода строится (k+1) – е приближение по следующим формулам:
корней известно, тогда в соответствии с идеей метода строится (k+1) – е приближение по следующим формулам:
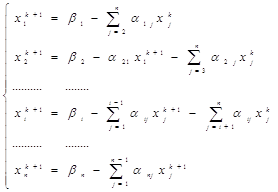
|
Если выполняется достаточное условие сходимости для системы (5) – по строкам, то в методе Зейделя выгодно расположить уравнения (6) так, чтобы первое уравнение системы имело наименьшую сумму модулей коэффициентов: ![]() .
.
Теперь рассмотри 3 метод – метод верхних релаксаций.
Метод верхней релаксации – это есть метод Зейделя с заданным числовым параметром w.
Одним из наиболее распространенных одношаговых методов является метод верхних релаксаций, который имеет следующий вид ![]() (7), где w заданный числовой параметр (0<w<2). Изменяя w можно получать различную скорость сходимости итерационного процесса. Этот параметр выбирается таким образом, чтобы на каждом шаге итерационного процесса уменьшалась величина, характеризующая близость полученного решения к искомому решению системы.
(7), где w заданный числовой параметр (0<w<2). Изменяя w можно получать различную скорость сходимости итерационного процесса. Этот параметр выбирается таким образом, чтобы на каждом шаге итерационного процесса уменьшалась величина, характеризующая близость полученного решения к искомому решению системы.
Достоинством итерационного метода верхних релаксаций является то, что при его реализации программным путем алгоритм вычислений имеет простой вид и позволяет использовать всего один массив для неизвестного вектора.
Для получения расчетных формул (7) перепишем в виде: ![]() или в компонентной записи получим
или в компонентной записи получим ![]() (8) – это есть основная вычислительная формула.
(8) – это есть основная вычислительная формула.
В выражение (8) ![]() и
и ![]() входят одинаковым образом => при вычислениях они могут быть записаны в один и тот же массив. При реализации метода верхних релаксаций используется следующая форма записи алгоритма вычислений
входят одинаковым образом => при вычислениях они могут быть записаны в один и тот же массив. При реализации метода верхних релаксаций используется следующая форма записи алгоритма вычислений ![]() .
.
Действительно, при последовательном нахождении элемента ![]() (i+10 итерации) на каждом шаге будут использоваться найденные ранее значения, которые при k<j соответствуют i+1 итерации, а при k<j-i итерации.
(i+10 итерации) на каждом шаге будут использоваться найденные ранее значения, которые при k<j соответствуют i+1 итерации, а при k<j-i итерации.
Применение метода к конкретной задаче (анализ)
Составляя задачи на языке программирования Borland C++ Builder 6 для реализации точных методов решения СЛАУ я учитывал разное количество уравнений в системе (размерность матрицы задавал равным nxn). Но для проверки результатов использовал систему уравнений:
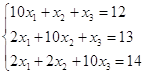
Вообще говоря, процесс Зейделя сходится быстрее, чем метод Якоби. Бывает, что процесс Зейделя сходится, когда простая итерация расходится и т.п. Правда, бывает и наоборот. Во всяком случае, достаточные условия сходимости для метода Якоби достаточны и для сходимости метода Зейделя. Реализовав программы из полученного ответа я увидел, что процесс Зейделя сходится быстрее. Это видно по количеству итераций полученных в программе при приближенной точности ![]() =0,000001. Если для метода Якоби они составляют 16, то для метода Зейделя они составляют 9.
=0,000001. Если для метода Якоби они составляют 16, то для метода Зейделя они составляют 9.
Также рассматривая метод верхней релаксации и сравнивая его с двумя другими методами видно, что в методе верхней релаксации количество итераций зависит от заданного числового параметра w. Задавая w=1, количество итераций равно 9, уменьшая значение параметра от 1 количество итераций начинает расти, в свою очередь увеличивая параметр количество итераций тоже начинает расти.
Приведем таблицу показывающих количество итераций (k) при разных значениях параметра w:
| w | 0.1 | 0.4 | 0.8 | 0.9 | 1 | 1.1 | 1.2 | 1.3 | 1.7 | 1.9 |
| k | 16 | 15 | 14 | 13 | 9 | 13 | 14 | 15 | 16 | 16 |
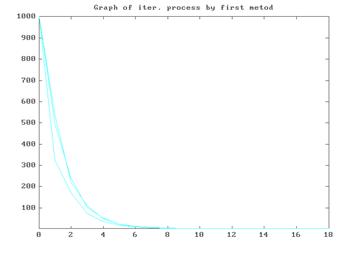
Из всего этого можно сделать вывод, что итерационные методы сходятся быстрее, чем точные методы, о чем свидетельствуют как быстрое уменьшение невязок, так и уменьшение изменений неизвестных.
Листинг программы
// –
#include <vcl.h>
#pragma hdrstop
#include «Unit1.h»
// –
#pragma package (smart_init)
#pragma resource «*.dfm»
#include<math.h>
#include<stdlib.h>
TForm1 *Form1;
int n=0, prov=0, k=0;
const x=100;
float A[x] [x], B[x] [x];
float C[x], Y[x];
float *X;
bool fl1=false;
float e;
float v_sh;
// –
__fastcall TForm1:TForm1 (TComponent* Owner)
: TForm(Owner)
{
}
// –
void __fastcall TForm1: ButtonOkClick (TObject *Sender)
{
Memo1->Lines->Clear();
k=0;
TryStrToInt (Edit1->Text, n);
if (n>1)
{
StringGrid1->Enabled=true;
StringGrid1->RowCount=n;
StringGrid1->ColCount=n+1;
ButtonClear->Enabled=true;
ButtonOk->Enabled=false;
StringGrid1->Color=clWindow;
ButtonYakobi->Enabled=true;
ButtonZeydel->Enabled=true;
ButtonRelax->Enabled=true;
X=new float[n];
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
A[i] [j]=NULL;
}
X[i]=NULL;
}
}
else
{
ShowMessage («Число должно быть вещественного типа!»);
}
}
// –
void __fastcall TForm1: ButtonClearClick (TObject *Sender)
{
StringGrid1->Enabled=false;
StringGrid1->RowCount=0;
StringGrid1->ColCount=0;
ButtonClear->Enabled=false;
ButtonOk->Enabled=true;
StringGrid1->Color=clBtnFace;
ButtonYakobi->Enabled=false;
}
// –
void __fastcall TForm1: ButtonYakobiClick (TObject *Sender)
{
//TryStrToFloat (Edit2->Text, e);
Memo1->Lines->Clear();
e=StrToFloat (Edit2->Text);
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
TryStrToFloat (StringGrid1->Cells[j] [i], A[i] [j]);
}
}
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
if (A[i] [j]==NULL)
{
ShowMessage («Ошибка! Есть пустые ячейки!»);
fl1=true;
i=n;
break;
}
}
}
if(! fl1) {
for (int i=0; i<n; i++)
{
for (int j=0; j<n; j++)
{
if (i!=j) B[i] [j]=(-1)*A[i] [j]/A[i] [i];
else
{
B[i] [j]=0;
C[i]=A[i] [n]/A[i] [i];
}
}
}
for (int i=0; i<n; i++) X[i]=C[i];
float s=0;
k=0;
do
{
prov=0;
for (int i=0; i<n; i++)
{
Y[i]=X[i];
for (int j=0; j<n; j++)
{
s+=B[i] [j]*X[i];
}
X[i]=s+C[i];
s=0;
}
for (int i=0; i<n; i++)
{
if (fabs(X[i] – Y[i])<e) prov++;
}
k++;
}
while (prov!=n);
Memo1->Lines->Add (» МЕТОД ЯКОБИ»);
Memo1->Lines->Add(«»);
String p=»»;
Memo1->Lines->Add («Промежуточная матрица:»);
for (int i=0; i<n; i++)
{
p=»»;
for (int j=0; j<n+1; j++)
{
p+=FloatToStr (B[i] [j])+»»;
}
Memo1->Lines->Add(p);
}
Memo1->Lines->Add(«»);
Memo1->Lines->Add («Корни СЛАУ равны:»);
for (int i=0; i<n; i++)
{
if (X[i]!=NULL)
{
Memo1->Lines->Add («x»+IntToStr (i+1)+» = «+FloatToStr (X[i]));
}
else
{
Memo1->Lines->Add («Нет корней!»);
break;
}
}
Memo1->Lines->Add(«»);
Memo1->Lines->Add («Количество итераций = «+FloatToStr(k));
}
}
// –
void __fastcall TForm1: ButtonExitClick (TObject *Sender)
{
Close();
}
// –
void __fastcall TForm1: RadioButton2Click (TObject *Sender)
{
ButtonYakobi->Visible=false;
ButtonZeydel->Visible=true;
ButtonRelax->Visible=false;
}
// –
void __fastcall TForm1: RadioButton1Click (TObject *Sender)
{
ButtonYakobi->Visible=true;
ButtonZeydel->Visible=false;
ButtonRelax->Visible=false;
}
// –
void __fastcall TForm1: ButtonZeydelClick (TObject *Sender)
{
Memo1->Lines->Clear();
k=0;
e=StrToFloat (Edit2->Text);
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
TryStrToFloat (StringGrid1->Cells[j] [i], A[i] [j]);
}
}
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
if (A[i] [j]==NULL)
{
ShowMessage («Ошибка! Есть пустые ячейки!»);
fl1=true;
i=n;
break;
}
}
}
if(! fl1) {
for (int i=0; i<n; i++)
{
for (int j=0; j<n; j++)
{
if (i!=j) B[i] [j]=(-1)*A[i] [j]/A[i] [i];
else
{
B[i] [j]=0;
C[i]=A[i] [n]/A[i] [i];
}
}
}
for (int i=0; i<n; i++)
{
X[i]=rand();
}
k=0;
float s=0;
for (int i=0; i<n; i++)
{
for (int j=0; j<n; j++)
{
s+=B[i] [j];
}
Y[i]=s;
s=0;
}
s=Y[0];
for (int i=1; i<n; i++)
{
if (s<Y[i]) s=Y[i];
Y[i]=0;
}
if (s<1)
{
do
{
s=0;
for (int i=0; i<n; i++)
{
Y[i]=X[i];
}
for (int i=0; i<n; i++)
{
s=C[i];
for (int j=0; j<n; j++)
{
s+=X[j]*B[i] [j];
}
X[i]=s;
}
prov=0;
for (int i=0; i<n; i++)
{
if (fabs(X[i] – Y[i])<e) prov++;
}
k++;
}
while (prov!=n);
Memo1->Lines->Add (» МЕТОД ЗЕЙДЕЛЯ»);
Memo1->Lines->Add(«»);
String p=»»;
Memo1->Lines->Add («Промежуточная матрица:»);
for (int i=0; i<n; i++)
{
p=»»;
for (int j=0; j<n+1; j++)
{
p+=FloatToStr (B[i] [j])+»»;
}
Memo1->Lines->Add(p);
}
Memo1->Lines->Add(«»);
Memo1->Lines->Add («Корни СЛАУ равны:»);
for (int i=0; i<n; i++)
{
if (X[i]!=NULL)
{
Memo1->Lines->Add («x»+IntToStr (i+1)+» = «+FloatToStr (X[i]));
}
else
{
Memo1->Lines->Add («Нет корней!»);
break;
}
}
Memo1->Lines->Add(«»);
Memo1->Lines->Add («Количество итераций = «+FloatToStr(k));
}
else {Memo1->Lines->Add («СЛАУ является не сходимой!»);}
}
}
// –
void __fastcall TForm1: RadioButton3Click (TObject *Sender)
{
ButtonYakobi->Visible=false;
ButtonZeydel->Visible=false;
ButtonRelax->Visible=true;
}
// –
void __fastcall TForm1: ButtonRelaxClick (TObject *Sender)
{
//TryStrToFloat (Edit2->Text, e);
v_sh=StrToFloat (Edit3->Text);
e=StrToFloat (Edit2->Text);
Memo1->Lines->Clear();
k=0;
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
TryStrToFloat (StringGrid1->Cells[j] [i], A[i] [j]);
}
}
for (int i=0; i<n; i++)
{
for (int j=0; j<n+1; j++)
{
if (A[i] [j]==NULL)
{
ShowMessage («Ошибка! Есть пустые ячейки!»);
fl1=true;
i=n;
break;
}
}
}
if(! fl1) {
float vsp=0, alp=0;
for (int i=0; i<n; i++)
{
for (int j=0; j<n; j++)
{
if (i!=j) B[i] [j]=(-1)*A[i] [j]/A[i] [i];
else
{
B[i] [j]=0;
C[i]=A[i] [n]/A[i] [i];
}
}
}
float *sq_z=new float[n];
float *sq_y=new float[n];
for (int i=0; i<n; i++)
{
sq_z[i]=rand();
}
for (int i=0; i<n; i++) sq_y[i]=C[i];
for (int i=0; i<n; i++) X[i]=0;
vsp=C[0];
for (int j=0; j<n; j++)
{
vsp+=sq_z[j]*B[0] [j];
}
sq_z[0]=vsp;
for (int i=0; i<n; i++)
{
for (int j=0; j<n; j++)
{
vsp+=B[i] [j];
}
Y[i]=vsp;
vsp=0;
}
vsp=Y[0];
for (int i=1; i<n; i++)
{
if (vsp<Y[i]) vsp=Y[i];
Y[i]=0;
}
if (vsp<1)
{
do
{
for (int i=0; i<n; i++)
{
Y[i]=X[i];
}
for (int i=0; i<n; i++)
{
vsp=C[i];
for (int j=0; j<n; j++)
{
vsp+=sq_z[j]*B[i] [j];
alp+=B[i] [j]*sq_y[i];
}
sq_z[i]=vsp;
sq_y[i]=alp+C[i];
vsp=0;
alp=0;
X[i]=v_sh*sq_z[i]+(1-v_sh)*sq_y[i];
}
prov=0;
for (int i=0; i<n; i++)
{
if (fabs(X[i] – Y[i])<e) prov++;
}
k++;
}
while (prov!=n);
Memo1->Lines->Add (» МЕТОД ВЕРХНЕЙ РЕЛАКСАЦИИ»);
Memo1->Lines->Add(«»);
String p=»»;
Memo1->Lines->Add («Промежуточная матрица:»);
for (int i=0; i<n; i++)
{
p=»»;
for (int j=0; j<n+1; j++)
{
p+=FloatToStr (B[i] [j])+»»;
}
Memo1->Lines->Add(p);
}
Memo1->Lines->Add(«»);
Memo1->Lines->Add («Корни СЛАУ равны:»);
for (int i=0; i<n; i++)
{
if (X[i]!=NULL)
{
Memo1->Lines->Add («x»+IntToStr (i+1)+» = «+FloatToStr (X[i]));
}
else
{
Memo1->Lines->Add («Нет корней!»);
break;
}
}
Memo1->Lines->Add(«»);
Memo1->Lines->Add («Количество итераций = «+FloatToStr(k));
}
else {Memo1->Lines->Add («СЛАУ является не сходимой!»);}
}
}
// –
Результаты расчета
| МЕТОД ЯКОБИ | МЕТОД ЗЕЙДЕЛЯ | МЕТОД ВЕРХНЕЙ РЕЛАКСАЦИИ |
| Промежуточная матрица: 0 -0,100000001490 -0,100000001490 0 -0,200000002980 0 -0,100000001490 0 -0,200000002980 -0,200000002980 0 0
Корни СЛАУ равны: x1 = 1 x2 = 1 x3 = 1,00000011920929
Количество итераций = 16 | Промежуточная матрица: 0 -0,100000001490 -0,100000001490 0 -0,200000002980 0 -0,100000001490 0 -0,200000002980 -0,200000002980 0 0
Корни СЛАУ равны: x1 = 1 x2 = 0,99999988079071 x3 = 0,999999940395355
Количество итераций = 9 | Промежуточная матрица: 0 -0,100000001490 -0,100000001490 0 -0,200000002980 0 -0,100000001490 0 -0,200000002980 -0,200000002980 0 0
Корни СЛАУ равны: x1 = 1,00000011920929 x2 = 0,99999988079071 x3 = 0,999999940395355
w=1
Количество итераций = 9 |
Похожие работы
... матрицы могут вычисляться по следующим формулам: 6. Метод квадратного корня Использование разложения на взаимно транспонированные треугольные матрицы при решении систем алгебраических уравнений называется метод квадратного корня. Метод разложения на транспонированные треугольные матрицы имеет модификацию, заключающуюся в выделении в произведении диагональной матрицы D с элементами на ...
... , но выбор перехода к системе x=(x) зависит от типа конкретной решаемой системы линейных алгебраических уравнений. 6. Заключение В данной курсовой работе был реализован метод простой итерации для решения систем линейных алгебраических уравнений в виде двух программ, каждая из которых использует свой собственный способ перехода от системы вида F(x)=x к системе вида x=(x). Вообще говоря, ...
... 1.2 0.4 -0.8 -0.8 3.6 4 4.7 10.4 9.7 9.7 -8.4Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = ...
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...
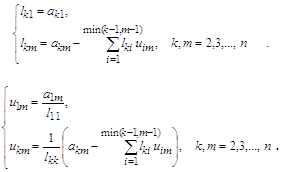
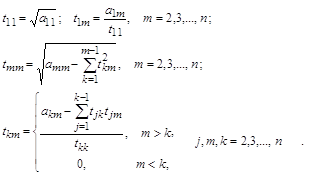
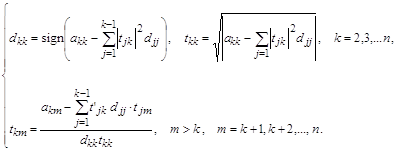
0 комментариев