Навигация
Метод простой итерации для решения систем линейных алгебраических уравнений
Министерство науки и образования РФ
Новосибирский государственный технический университетКафедра экономической информатики
Курс: "Численные методы" Пояснительная записка к курсовой работе на тему "Метод простой итерации для решения систем линейных алгебраических уравнений"Факультет: Бизнеса
Преподаватель: Сарычева О. М.
Новосибирск, 2010
Содержание
1. Введение
2. Математическая постановка задачи и описание метода
3. Описание программного обеспечения
3.1 Общие сведения
3.2 Функциональное назначение программы
3.3 Вызов и загрузка программы
3.4 Входные данные
3.5 Выходные данные
3.6 Описание алгоритмов
3.6.1 Программный модуль metod1.m
3.6.2 Программный модуль metod2.m
3.7 Используемые программные и технические средства
4. Описание тестовых задач
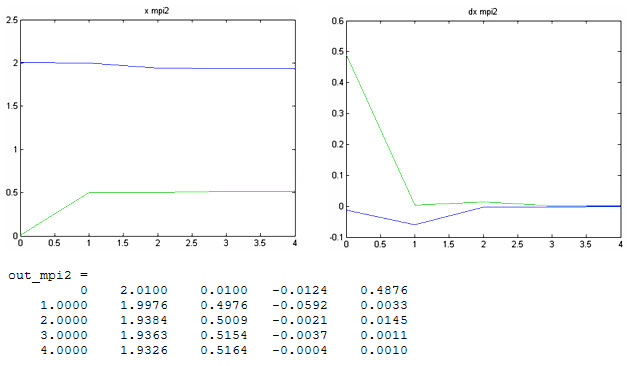
5. Анализ результатов счета, выводы
6. Заключение
Приложения
Список литературы
1. Введение
В данной курсовой работе необходимо рассмотреть один из множества существующих итерационных методов - метод простой итерации для решения систем линейных алгебраических уравнений.
Прежде чем говорить о вышеуказанном методе, дадим краткую характеристику вообще итерационным методам.
Итерационные методы дают возможность найти решение системы, как предел бесконечного вычислительного процесса, позволяющего по уже найденным приближениям к решению построить следующее, более точное приближение. Привлекательной чертой таких методов является их самоисправляемость и простота реализации на ЭВМ. Если в точных методах ошибка в вычислениях, когда она не компенсируется случайно другими ошибками, неизбежно ведет к ошибкам в результате, то в случае сходящегося итерационного процесса ошибка в каком-то приближении исправляется в последующих вычислениях, и такое исправление требует, как правило, только нескольких лишних шагов единообразных вычислений. Итерационный метод, для того чтобы начать по нему вычисления, требует знания одного или нескольких начальных приближений к решению.
Условия и скорость сходимости каждого итерационного процесса существенно зависят от свойств уравнений, то есть от свойств матрицы системы, и от выбора начальных приближений.
2. Математическая постановка задачи и описание метода
2.1 Математическая постановка задачи
Исследовать метод простой итерации для решения систем линейных алгебраических уравнений, а именно: влияние способа перехода от системы F(x)=x к системе x=![]() (x) на точность полученного решения, скорость сходимости метода, время счета, число операций.
(x) на точность полученного решения, скорость сходимости метода, время счета, число операций.
2.2 Описание метода
Пусть дана система линейных алгебраических уравнений в виде Ax=b (2.2.1).
Пусть (2.2.1.) приведена каким-либо образом к виду x=Cx+f (2.2.2), где C - некоторая матрица, f - вектор-столбец. Исходя из произвольного вектора
 x01
x01
x( 0 )= x02
x03
строим итерационный процесс x( k+1 )=Cx( k )+f (k=0,1,2,3,…) или в развернутой форме
![]()
x1 ( k+1 ) = c11 x1( k ) + c12 x2( k ) + …+ c1n xn( k ) + f1 , (2.2.3)
xn ( k+1 ) = cn1 x1( k ) + cn2 x2( k ) + …+ 1nn xn( k ) + fn .
Производя итерации, получим последовательность векторов x( 1 ), x( 2),…, x( k ),… Доказано, что если элементы матрицы C удовлетворяют одному из условий
![]() (i=1,2,…,n) (2.2.4)
(i=1,2,…,n) (2.2.4)
![]() (j=1,2,…,n) (2.2.5),
(j=1,2,…,n) (2.2.5),
то процесс итерации сходится к точному решению системы x при любом начальном векторе x(0), то есть
![]() x=
x=![]() x( k ) .
x( k ) .
Таким образом, точное решение системы получается лишь в результате бесконечного процесса, и всякий вектор x(k) из полученной последовательности является приближенным решением. Оценка погрешности этого приближенного решения x(k) дается одной из следующих формул:
| xi- xi( k ) | ![]()
![]() | xi( k ) - xi( k -1 )|, (2.2.4')
| xi( k ) - xi( k -1 )|, (2.2.4')
если выполнено условие (2.2.4), или
| xi- xi( k ) | ![]()
![]() | xi( k ) - xi( k -1 )|, (2.2.5')
| xi( k ) - xi( k -1 )|, (2.2.5')
если выполнено условие (2.2.5). Эти оценки можно еще усилить соответственно так:
max | xi- xi( k ) | ![]()
![]() | xi( k ) - xi( k -1 )|, (2.2.4'')
| xi( k ) - xi( k -1 )|, (2.2.4'')
или
![]() | xi- xi( k ) |
| xi- xi( k ) | ![]()
![]() | xi( k ) - xi( k -1 )|. (2.2.5'')
| xi( k ) - xi( k -1 )|. (2.2.5'')
Процесс итераций заканчивают, когда указанные оценки свидетельствуют о достижении заданной точности.
Начальный вектор x( 0 ) может быть выбран, вообще говоря, произвольно. Иногда берут x( 0 )=f. Однако, наиболее целесообразно в качестве компонент вектора x( 0 ) взять приближенные значения неизвестных, полученные грубой прикидкой.
Приведение системы (2.2.1) к виду (2.2.2) можно осуществить различными способами. Важно только, чтобы выполнялось одно из условий (2.2.4) или (2.2.5). Ограничимся рассмотрением двух таких способов.
Первый способ. Если диагональные элементы матрицы А отличны от нуля, то есть
aii![]() 0 ( i=1,2,…,n),
0 ( i=1,2,…,n),
то систему (2.2.1) можно записать в виде
![]() x1=
x1=![]() (b1 - a12 x2 - … - a1n xn ),
(b1 - a12 x2 - … - a1n xn ),
x2=![]() (b2 - a21 x1 - a23 x3 -… - a2n xn ), (2.2.6)
(b2 - a21 x1 - a23 x3 -… - a2n xn ), (2.2.6)
xn=![]() (bn - an1 x1 - … - an n-1 xn-1 ).
(bn - an1 x1 - … - an n-1 xn-1 ).
В этом случае элементы матрицы С определяются следующим образом:
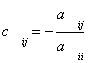 (i
(i![]() j), cii=0,
j), cii=0,
и тогда условия (2.2.4) и (2.2.5) соответственно приобретают вид
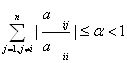 (i=1,2,… ,n), (2.2.7)
(i=1,2,… ,n), (2.2.7)
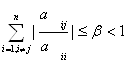 (j=1,2,… ,n). (2.2.8)
(j=1,2,… ,n). (2.2.8)
Неравенства (2.2.7), (2.2.8) будут выполнены, если диагональные элементы матрицы А удовлетворяют условию
![]() (i=1,2,… ,n), (2.2.9)
(i=1,2,… ,n), (2.2.9)
то есть если модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов (не считая свободных членов).
Второй способ позволяет записать систему (2.2.1) в виде
![]() x1 = b1 - (a11 -1)x1 - a12 x2 - … - a1n xn ,
x1 = b1 - (a11 -1)x1 - a12 x2 - … - a1n xn ,
x2 = b2 - a21 x1 -(a22 -1)x2 -… - a2n xn , (2.2.10)
xn = bn - an1 x1 - an2 x2 -… -(ann -1)xn .
и пояснений не требует.
3. Описание программного обеспечения
3.1 Общие сведения
Данное программное обеспечение представлено в виде двух основных программных модулей (файлы metod1.m и metod2.m) и четырех вспомогательных модулей (файлы system_a.m, system_b.m, x0.m и x_ok.m).
3.2 Функциональное назначение программы
Данное программное обеспечение предназначено для решения систем линейных алгебраических уравнений вида Ax=b методом простой итерации.
Программный модуль metod1.m содержит непосредственно алгоритм решения систем линейных алгебраических уравнений методом простой итерации, использующий первый способ перехода от системы вида F(x)=x к системе вида x=![]() (x) (см. п.2.2.).
(x) (см. п.2.2.).
Программный модуль metod2.m также содержит непосредственно алгоритм решения систем линейных алгебраических уравнений методом простой итерации, но использующий второй способ перехода от системы вида F(x)=x к системе вида x=![]() (x) (см. п.2.2.).
(x) (см. п.2.2.).
Вспомогательный модуль system_a.m содержит матрицу А исходной системы линейных алгебраических уравнений вида Ax=b.
Вспомогательный модуль system_b.m содержит столбец b исходной системы линейных алгебраических уравнений вида Ax=b.
Вспомогательный модуль x0.m содержит столбец начального приближения к точному решению исходной системы линейных алгебраических уравнений вида Ax=b.
Вспомогательный модуль x_ok.m содержит столбец точного решения исходной системы линейных алгебраических уравнений вида Ax=b.
Замечание: модули system_a.m, system_b.m, x0.m всегда описывает сам пользователь, работающий с данным программным обеспечением, в зависимости от решаемой системы линейных алгебраических уравнений.
Модуль x_ok.m также может быть описан пользователем, но он не является обязательным, так как точного решения обычно у пользователя нет. Отсутствие данного модуля не влияет на правильность работы программы, он является вспомогательным и необходим лишь для оценки погрешности полученного решения (как этого требует задание), но что обычно не нужно в прикладном использовании данного программного обеспечения.
3.3 Вызов и загрузка программы
Для вызова программы на выполнение необходимо загрузить программу MatLab 3.5f (и выше), затем в командной строке данной среды набрать имя одного из программных модулей (metod1.m или metod2.m).
3.4 Входные данные
1. system_а - матрица А исходной системы линейных алгебраических уравнений вида Ax=b, считывающаяся из модуля system_а.m;
2. system_b - столбец b исходной системы линейных алгебраических уравнений вида Ax=b, считывающийся из модуля system_b.m;
3. x0 - столбец начальных приближений, считывающийся из модуля x0.m;
4. x_ok - столбец точного решения исходной системы линейных алгебраических уравнений вида Ax=b, считывающийся из модуля x_ok.m.
Замечание: если отсутствует модуль x_ok.m, то переменная x_ok не передается в основные программные модули.
3.5 Выходные данные
Выходными данными программных модулей metod1.m и metod2.m является файл total - файл-отчет, содержащий результаты одного или нескольких итерационных процессов, а именно: полученные решения, погрешности полученного решения, скорость сходимости метода, время счета, число операций.
Похожие работы
... 1.2 0.4 -0.8 -0.8 3.6 4 4.7 10.4 9.7 9.7 -8.4Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = ...
... 10.4 9.7 9.7 -8.4 Результат вычислений по методу Гаусса x1 = 5.0000000000E+00 x2 = -4.0000000000E+00 x3 = 3.0000000000E+00 x4 = -2.0000000000E+00 2.2 Программа решения систем линейных уравнений по методу Зейделя 2.2.1. Постановка задачи. Требуется решить систему линейных алгебраических уравнений с вещественными коэффициентами вида a11x1 + a12x2 + … + a1nxn = b1 , a21x2 + ...
... 1040, мы все еще получаем сходимость, при количестве итераций порядка 130. 4 Анализ результатов, выводы Целью нашего исследование было сравнение методов простой итерации и Ньютона для решения систем из двух нелинейных уравнений по числу итераций, времени сходимости в зависимости от выбора начального приближения к решению и допустимой ошибки. Зависимость этих параметров от выбора начального ...
... конкретной задаче (анализ) Составляя задачи на языке программирования Borland C++ Builder 6 для реализации точных методов решения СЛАУ я учитывал разное количество уравнений в системе (размерность матрицы задавал равным nxn). Но для проверки результатов использовал систему уравнений: Вообще говоря, процесс Зейделя сходится быстрее, чем метод Якоби. Бывает, что процесс Зейделя сходится, ...



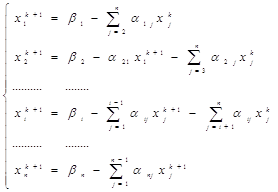
0 комментариев