Навигация
Якщо до наявних двох точок розбиття додати нові точки, то нижня сума Дарбу-Стілтьєса може від цього лише зрости, а верхня сума – лише зменшитися
1. Якщо до наявних двох точок розбиття додати нові точки, то нижня сума Дарбу-Стілтьєса може від цього лише зрости, а верхня сума – лише зменшитися.
2. Кожна нижня сума Дарбу-Стілтьєса не перебільшує кожної верхньої суми, хоча б і такій, що відповідає іншому розбиттю проміжку.
Якщо ввести нижній і верхній інтеграли Дарбу-Стілтьєса:
![]() =
=![]() і
і ![]() ,
,
то виявляється, що ![]() .
.
Нарешті, за допомогою сум Дарбу-Стілтьєса легко встановити для випадку, що розглядається, основну ознаку існування інтегралу Стілтьєса:
Теорема. Для існування інтегралу Стілтьєса необхідно і достатньо, щоб виконувалося
![]() , або
, або ![]() , (4)
, (4)
якщо під ![]() , як зазвичай, розуміти коливання
, як зазвичай, розуміти коливання ![]() функції
функції ![]() в
в ![]() -му проміжку
-му проміжку ![]() .
.
2.2 Класи випадків існування інтегралу Стілтьєса
1. Якщо функція ![]() а функція
а функція ![]() має обмежену зміну, то інтеграл Стілтьєса
має обмежену зміну, то інтеграл Стілтьєса
![]() (5)
(5)
існує.
Спочатку припустимо, що ![]() монотонно зростає, тоді за довільно заданим
монотонно зростає, тоді за довільно заданим ![]() , враховуючи рівномірну неперервність функції
, враховуючи рівномірну неперервність функції ![]() , знайдеться таке
, знайдеться таке ![]() , що на будь-якому проміжку, довжина якого менше
, що на будь-якому проміжку, довжина якого менше ![]() , коливання
, коливання ![]() буде менше за
буде менше за ![]() . Нехай тепер проміжок
. Нехай тепер проміжок ![]() розбитий на частини так, що
розбитий на частини так, що ![]() . Тоді всі
. Тоді всі ![]() <
<![]() і
і
![]() ,
,
звідки й слідує виконання умови (4), а, отже, і існування інтеграла також.
У загальному випадку, якщо функція ![]() має обмежену зміну, її можна представити у вигляді двох зростаючих обмежених функцій:
має обмежену зміну, її можна представити у вигляді двох зростаючих обмежених функцій: ![]() . У відповідності до цього, перетворюється і сума Стілтьєса, що відповідає функції
. У відповідності до цього, перетворюється і сума Стілтьєса, що відповідає функції ![]() :
:
![]()
Так, за вже доведеним, кожна із сум ![]() і
і ![]() при
при ![]() прямує до граничної межі, це справедливо і відносно суми
прямує до граничної межі, це справедливо і відносно суми ![]() , що і треба було довести.
, що і треба було довести.
Можна послабити умови, що накладаються на функцію ![]() якщо одночасно посилити вимоги до функції
якщо одночасно посилити вимоги до функції ![]() :
:
2. Якщо функція ![]() інтегровна на проміжку
інтегровна на проміжку ![]() за Ріманом, а
за Ріманом, а ![]() задовольняє умові Ліпшиця:
задовольняє умові Ліпшиця:
![]() (6)
(6)
![]() ,
,
то інтеграл (5) існує.
Для того, щоб знов мати можливість застосувати встановлений вище критерій, припустимо спочатку функцію ![]() як таку, що не лише задовольняє умові (6), але і монотонно зростаючу.
як таку, що не лише задовольняє умові (6), але і монотонно зростаючу.
Враховуючи (6), очевидно ![]() , так, що
, так, що
![]()
Але остання сума при ![]() і сама прямує до нуля, як наслідок інтегровності (за Ріманом) функції
і сама прямує до нуля, як наслідок інтегровності (за Ріманом) функції ![]() , а тоді прямує до нуля і перша сума, що доводить існування інтеграла (5).
, а тоді прямує до нуля і перша сума, що доводить існування інтеграла (5).
У загальному випадку функції ![]() , що задовольняє умові Ліпшиця (6), представимо її у вигляді різниці
, що задовольняє умові Ліпшиця (6), представимо її у вигляді різниці
![]() =
=![]() .
.
Функція ![]() =
=![]() , очевидно, задовольняє умові Ліпшиця, і в той же час монотонно зростає. Теж саме справедливо і для функції
, очевидно, задовольняє умові Ліпшиця, і в той же час монотонно зростає. Теж саме справедливо і для функції ![]() =
=![]() , так як в силу (6), при
, так як в силу (6), при ![]()
![]() і
і
![]() .
.
У такому випадку міркування завершено, як і в попередньому випадку.
3. Якщо функція ![]() інтегровна за Ріманом, а функцію
інтегровна за Ріманом, а функцію ![]() можна представити у вигляді інтеграла зі змінною верхнею межею інтегрування:
можна представити у вигляді інтеграла зі змінною верхнею межею інтегрування:
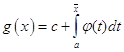 , (7)
, (7)
де ![]() абсолютно інтегровна на проміжку
абсолютно інтегровна на проміжку ![]() , то інтеграл (5) існує.
, то інтеграл (5) існує.
Нехай ![]() , так, що
, так, що ![]() монотонно зростає. Якщо
монотонно зростає. Якщо ![]() інтегровна за власним змістом, і виходячи з цього, обмежена:
інтегровна за власним змістом, і виходячи з цього, обмежена: ![]() , то для
, то для ![]() маємо
маємо 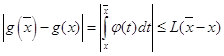 .
.
Таким чином, у цьому випадку ![]() задовольняє умові Ліпшиця, та інтеграл існує в силу (2).
задовольняє умові Ліпшиця, та інтеграл існує в силу (2).
Припустимо тепер, що ![]() інтегровна у невласному сенсі. Обмежимося випадком однієї особливої точки, скажімо
інтегровна у невласному сенсі. Обмежимося випадком однієї особливої точки, скажімо ![]() . Перш за все, за довільно взятим
. Перш за все, за довільно взятим ![]() вибираємо
вибираємо ![]() так, щоб було
так, щоб було
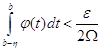 , (8)
, (8)
де ![]() - загальне коливання функції
- загальне коливання функції ![]() на розглядуваному нами проміжку.
на розглядуваному нами проміжку.
Розіб’ємо проміжок ![]() довільно на частини і складемо суму
довільно на частини і складемо суму
![]() .
.
Вона розкладається на дві суми ![]() , з яких перша відповідає проміжкам, що цілком містяться в проміжку
, з яких перша відповідає проміжкам, що цілком містяться в проміжку ![]() , а друга – решті проміжків. Останні, скоріш за все, містяться в проміжку
, а друга – решті проміжків. Останні, скоріш за все, містяться в проміжку ![]() , якщо тільки
, якщо тільки ![]() ; тоді в силу (8),
; тоді в силу (8),
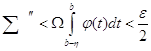 .
.
З іншого боку, так як на проміжку ![]() функція
функція ![]() інтегровна у власному сенсі, то за доведеним, при достатньо малому
інтегровна у власному сенсі, то за доведеним, при достатньо малому ![]() і сума
і сума ![]() стане меншою за
стане меншою за ![]() . Звідси слідує (4), що і потрібно було довести.
. Звідси слідує (4), що і потрібно було довести.
У загальному випадку, коли функція ![]() абсолютно інтегровна на проміжку
абсолютно інтегровна на проміжку ![]() , ми розглянемо функції
, ми розглянемо функції
![]()
![]() ,
,
очевидно, невід’ємні і інтегровні на даному проміжку. Так як
![]() ,
,
то питання зводиться до вже розглянутого випадку.
ЗАУВАЖЕННЯ. Нехай функція ![]() неперервна на проміжку
неперервна на проміжку ![]() і має, виключаючи лише скінчене число точок, похідну
і має, виключаючи лише скінчене число точок, похідну ![]() , причому ця похідна інтегровна (у власному чи невласному змісті) від
, причому ця похідна інтегровна (у власному чи невласному змісті) від ![]() до
до ![]() ; тоді, як відомо, має місце формула (7):
; тоді, як відомо, має місце формула (7):
![]() .
.
Якщо ![]() абсолютно інтегровна, то до функції
абсолютно інтегровна, то до функції ![]() повністю справедливо все викладене в п. 3.[1;3]
повністю справедливо все викладене в п. 3.[1;3]
§3. Властивості інтегралу Стілтьєса
З визначення інтегралу Стілтьєса безпосередньо випливають такі його властивості:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]()
![]() .
.
При цьому у випадках 2, 3, 4 з існування інтегралів у правій частині випливає існування інтеграла у лівій частині. Далі маємо
5. ![]() ,
,
у припущенні, що ![]() і існують всі три інтеграли.
і існують всі три інтеграли.
Для доведення цієї формули достатньо включити точку с в число точок розбиття проміжку ![]() , при складанні суми Стілтьєса для інтегралу
, при складанні суми Стілтьєса для інтегралу ![]() .
.
Перш за все, з існування інтеграла ![]() уже випливає існування обох інтегралів
уже випливає існування обох інтегралів ![]() і
і ![]()
![]()
![]() .
.
Для своєрідного граничного процесу, за допомогою якого для стілтьєсової суми отримується інтеграл Стілтьєса, має місце принцип збіжності Больцано-Коші. Таким чином по заданому ![]() враховуючи існування інтеграла
враховуючи існування інтеграла ![]() знайдеться таке
знайдеться таке ![]() , що будь-які дві суми
, що будь-які дві суми ![]() і
і ![]() , яким відповідають
, яким відповідають ![]() і
і ![]() , різняться менш ніж на
, різняться менш ніж на ![]() . Якщо при цьому у склад точок розбиття включити точку с, а точки розбиття, що припадають на проміжок
. Якщо при цьому у склад точок розбиття включити точку с, а точки розбиття, що припадають на проміжок ![]() , брати в обох випадках одними й тими самими, то різниця
, брати в обох випадках одними й тими самими, то різниця ![]() зведеться до різниці
зведеться до різниці ![]() двох сум Стілтьєса, що належать вже проміжку
двох сум Стілтьєса, що належать вже проміжку ![]() , бо решта доданків взаємно скорочуються. Застосовуючи до проміжку
, бо решта доданків взаємно скорочуються. Застосовуючи до проміжку ![]() і обрахованим для нього стілтьєсовим сумам той же принцип збіжності, зробимо висновок про існування інтеграла
і обрахованим для нього стілтьєсовим сумам той же принцип збіжності, зробимо висновок про існування інтеграла ![]() . Аналогічним чином встановлюється і існування інтегралу
. Аналогічним чином встановлюється і існування інтегралу ![]() . Але, важливо відмітити, що з існування обох інтегралів
. Але, важливо відмітити, що з існування обох інтегралів ![]() і
і ![]() , взагалі кажучи, не випливає існування інтегралу
, взагалі кажучи, не випливає існування інтегралу ![]() . Щоб упевнитися в цьому, достатньо розглянути приклад. Нехай на проміжку
. Щоб упевнитися в цьому, достатньо розглянути приклад. Нехай на проміжку ![]() функції
функції ![]() і
і ![]() задані наступними рівностями:
задані наступними рівностями:
![]()
![]()
![]()
Легко побачити, що інтеграли
![]()
обидва існують і рівні 0, бо відповідні суми Стілтьєса всі рівні 0: для першого це випливає з того, що завжди ![]() =0, для другого – з постійності функції
=0, для другого – з постійності функції ![]() , завдяки чому
, завдяки чому ![]() =0.
=0.
У той же час інтеграл ![]() не існує. Дійсно, розіб’ємо проміжок
не існує. Дійсно, розіб’ємо проміжок ![]() так, щоб точка 0 не потрапила у склад точок розбиття, і складемо суму:
так, щоб точка 0 не потрапила у склад точок розбиття, і складемо суму:
![]() .
.
Якщо точка 0 потрапляє в проміжок ![]() , так, що
, так, що ![]() , то в сумі
, то в сумі ![]() залишиться лише один
залишиться лише один ![]() -й доданок; решта будуть нулі, тому що
-й доданок; решта будуть нулі, тому що ![]() для
для ![]() . Отже,
. Отже,
![]() .
.
В залежності від того, чи буде ![]() або
або ![]() , виявиться
, виявиться ![]() або
або ![]() , так що
, так що ![]() границі не має
границі не має
Вказана своєрідна умова пов’язана з наявністю розривів у точці ![]() для обох функцій
для обох функцій ![]() і
і ![]() . [8]
. [8]
§4. Інтегрування за частинами
Для інтегралів Стілтьєса має місце формула
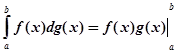 –
– ![]() (8)
(8)
в припущенні, що існує один з цих інтегралів; існування іншого звідси вже випливає. Ця формула носить назву формули інтегрування за частинами. Доведемо її.
Нехай існує інтеграл ![]() . Розклавши проміжок [а, b] на частини [xi , xi+1] (i = 0, 1, ..., n — 1), оберемо в цих частинах довільно по точці
. Розклавши проміжок [а, b] на частини [xi , xi+1] (i = 0, 1, ..., n — 1), оберемо в цих частинах довільно по точці ![]() таким чином, що
таким чином, що ![]()
Суму Стілтьєса для інтеграла ![]()
![]()
можна представити у вигляді
![]()
Якщо додати або відняти зправа вираз ![]() то
то ![]() перепишеться так:
перепишеться так:
![]()
Вираз у фігурних дужках представляє собою стілтьесову суму для інтеграла ![]() (існування якого припущено!). Вона відповідає розбиттю проміжку [а, b] точками ділення
(існування якого припущено!). Вона відповідає розбиттю проміжку [а, b] точками ділення ![]() якщо в якості обраних з проміжків
якщо в якості обраних з проміжків ![]() точок узяти xi, а для проміжків
точок узяти xi, а для проміжків ![]() , відповідно, а і b. Якщо, як зазвичай, покласти
, відповідно, а і b. Якщо, як зазвичай, покласти ![]() то тепер довжини всіх частинних проміжків не перевищать
то тепер довжини всіх частинних проміжків не перевищать ![]() .
.
При ![]() сума у квадратних дужках прямує до
сума у квадратних дужках прямує до ![]() , з чого слідує, що існує границя і для
, з чого слідує, що існує границя і для ![]() , тобто інтеграл
, тобто інтеграл ![]() і цей інтеграл визначається формулою (9). [8]
і цей інтеграл визначається формулою (9). [8]
§5. Зведення інтеграла Стілтьєса до інтегралу Рімана
Нехай функція f(x) неперервна на проміжку [a, b], a g(x) монотонно зростає в цьому проміжку, і притому в суворому сенсі. Тоді, як показав Лебег (Н. Lebesgue), інтеграл Стілтьеса ![]() за допомогою підстановки
за допомогою підстановки ![]() безпосередньо зводиться до інтегралу Рімана.
безпосередньо зводиться до інтегралу Рімана.
Доведемо тепер, що
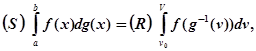 (10)
(10)
де останній інтеграл береться у звичайному сенсі, його існування забезпечено, так як функція g(v), а з нею і складна функція f(g-1(v)) неперервні.
Для цього розкладемо проміжок [а, b] на частини за допомогою точок ділення
a=x0<x1<…<xi<xi+1<…<xn=b
и складемо стілтьесову суму
![]()
Якщо покласти vi = g(xi) (i = 0, 1, . . ., n), то будемо мати
v0<v1< ... <vi< vi+1 < ... <vn = V.
Так як хi = g-1 (vi), то
![]()
Цей вираз має вигляд ріманової суми для інтеграла
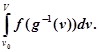
Маємо
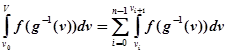 і
і
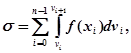
так що
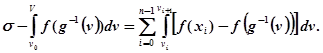
Припустимо тепер ![]() настільки малими, щоб коливання функції f(x) у всіх проміжках [xі, хі+1] були менше довільно наперед заданого числа
настільки малими, щоб коливання функції f(x) у всіх проміжках [xі, хі+1] були менше довільно наперед заданого числа ![]() > 0. Так як при
> 0. Так як при ![]() , очевидно,
, очевидно, ![]() , то одночасно і
, то одночасно і ![]() <
<![]() .
.
В такому випадку
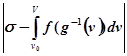 <
<![]()
Цим доведено, що
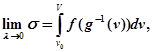
звідки и слідує (10). [4;6]
§6. Обчислення інтегралів Стілтьєса
Доведемо наступну теорему:
0 комментариев