Навигация
Якщо функція f(x) інтегрована в сенсі Рімана на проміжку [a, b], a g(x) представлена інтегралом
1. Якщо функція f(x) інтегрована в сенсі Рімана на проміжку [a, b], a g(x) представлена інтегралом
![]()
де функція ![]() абсолютно інтегровна в [а,b], то
абсолютно інтегровна в [а,b], то
![]() (11)
(11)
Існування інтеграла Стілтьєса при зроблених припущеннях уже було доведено вище.
Залишається лише з’ясувати рівність (11).
Без зменшення загальності можна припустити, що функція ![]() додатна.
додатна.
Складемо суму Стілтьєса
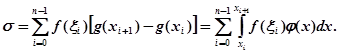
Так як, з іншого боку, можна написати
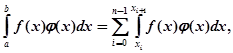
то будемо мати
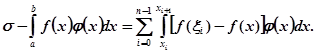
Очевидно, для ![]() буде
буде ![]() , де
, де ![]() означає коливання функції f(x) на проміжку [xі, xі+1]. Звідси витікає така оцінка записаної вище різниці:
означає коливання функції f(x) на проміжку [xі, xі+1]. Звідси витікає така оцінка записаної вище різниці:
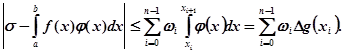
Нам відомо, що при ![]() остання сума прямує до 0, з чого слідує, що
остання сума прямує до 0, з чого слідує, що
![]() ,
,
що і доводить формулу (11).
2. При тих самих припущеннях стосовно функції f(x) припустимо, що функція g(x) неперервна на всьому проміжку [а, b] і має в ньому, за виключенням лише скінченої кількості точок, похідну g'(x), яка на [а, b] абсолютно інтегрована. Тоді
![]() (12)
(12)
Звертаючись до випадків, коли функція g(x) є розривною розглянемо спочатку «стандартну» розривну функцію р(х), яка визначається рівностями
![]()
Вона має розрив першого роду — стрибок — у точці х= 0 зправа, причому величина стрибка р(+0) – р(0)) дорівнює 1; в точці х =0 зліва і в решті точок функція p(x) неперервна. Функція p(x – c) буде мати такий самий розрив у точці x=c зправа; навпаки, p(с – x) буде мати подібний розрив у точці x=c зліва, причому величина стрибка дорівнює – 1.
Припустимо, що функція f(x) неперервна в точці х = с, і обчислимо інтеграл ![]() , де
, де ![]() (при
(при ![]() інтеграл рівний нулю).
інтеграл рівний нулю).
Складемо суму Стілтьєса:
![]() .
.
Нехай точка ![]() потрапляє, скажімо в
потрапляє, скажімо в ![]() -ий проміжок, так що
-ий проміжок, так що ![]() . Тоді
. Тоді ![]() , а при
, а при ![]() , очевидно
, очевидно ![]() . Таким чином, уся сума
. Таким чином, уся сума ![]() зводиться до одного доданку
зводиться до одного доданку ![]() . Нехай тепер
. Нехай тепер ![]() . По неперервності
. По неперервності ![]() . Виходячи з цього, існує (при
. Виходячи з цього, існує (при ![]() )
)
![]() (13)
(13)
Аналогічно можна упевнитися в тому, що (при ![]() )
)
![]() (14)
(14)
(при ![]() цей інтеграл перетворюється на нуль).
цей інтеграл перетворюється на нуль).
Тепер ми можемо довести дещо узагальнену на відміну від 2, а саме відмовимося від вимоги неперервності функції ![]() :
:
3. Нехай функція f(x) на проміжку ![]() неперервна,a g(x) має на цьому проміжку, виключаючи хіба лише скінчене число точок, похідну
неперервна,a g(x) має на цьому проміжку, виключаючи хіба лише скінчене число точок, похідну ![]() яка абсолютно інтегровна на
яка абсолютно інтегровна на ![]() . При цьому нехай функція g(x) у скінченому числі точок
. При цьому нехай функція g(x) у скінченому числі точок ![]()
має розрив першого роду. Тоді існує інтеграл Стілтъєса, який виражається формулою
![]()
![]() . (15)
. (15)
Характерна тут наявність позаінтегральної суми, де фігурують скачки функції g(x) в точках ![]() або
або ![]() — односторонні. (Якщо на будь-якій з цих функцій стрибка немає, то відповідний доданок суми перетворюється на нуль).
— односторонні. (Якщо на будь-якій з цих функцій стрибка немає, то відповідний доданок суми перетворюється на нуль).
Для спрощення запису введемо позначення для стрибків функції g(x) зправа и зліва:
![]()
![]() ,
,
![]()
![]() ;
;
очевидно, для ![]() ,
, ![]() .
.
Складемо допоміжну функцію:
![]() ,
,
Яка як би вбирає у себе усі розриви функції g(x), так що різниця ![]() , як ми зараз встановимо, виявляється вже неперервною.
, як ми зараз встановимо, виявляється вже неперервною.
Для значень ![]() відмінних від усіх
відмінних від усіх ![]() , неперервність функції
, неперервність функції ![]() не викликає сумнівів, бо для цих значень неперервні обидві функції
не викликає сумнівів, бо для цих значень неперервні обидві функції ![]() и
и ![]() . Доведемо тепер неперервність
. Доведемо тепер неперервність ![]() у точці
у точці ![]() зправа. Усі доданки суми
зправа. Усі доданки суми ![]() , окрім члена
, окрім члена ![]() , неперервну при
, неперервну при ![]() зправа, тому достатньо вивчити поведінку виразу
зправа, тому достатньо вивчити поведінку виразу ![]() . При
. При ![]() воно має значення
воно має значення ![]() ; але така ж і його границя при
; але така ж і його границя при ![]() :
:
![]() .
.
Аналогічно перевіряється ф неперервність функції ![]() в точці
в точці ![]() зліва.
зліва.
Далі, якщо взяти точку х (відмінну від усіх ![]() ), в якій функція
), в якій функція ![]() має похідну, то поблизу цієї точки
має похідну, то поблизу цієї точки ![]() зберігає постійне значення, виходячи з цього, у ній і функція
зберігає постійне значення, виходячи з цього, у ній і функція ![]() має похідну, причому
має похідну, причому ![]() .
.
Для неперервної функції ![]() , за попередньою теоремою, існує інтеграл Стілтьєса
, за попередньою теоремою, існує інтеграл Стілтьєса ![]() .
.
Так само легко обрахувати і інтеграл
![]()
![]()
![]()
![]() .
.
Додаючи почленно ці дві рівності, ми і прийдемо до рівності (15); існування інтеграла Стілтьєса від ![]() по функції
по функції ![]() встановлюється попутно. [5]
встановлюється попутно. [5]
§7. Приклади обчислення інтеграла Стілтьєса
1) Обчислити за формулою (11) інтеграл:
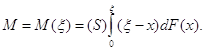
Розв’язок, (а)
![]() і т.д.
і т.д.
2) Обчислити за формулою (15) інтеграли:
(а) ![]() , де
, де 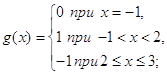
(б) ![]() , де
, де 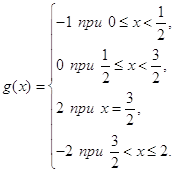
Розв’язок. (а) Функція ![]() має стрибок 1 при
має стрибок 1 при ![]() и стрибок —2 при
и стрибок —2 при ![]() ; в решті точок
; в решті точок ![]() . Тому
. Тому ![]()
(б) Стрибок 1 при ![]() и
и ![]() при
при ![]() (значення функції
(значення функції ![]() при
при ![]() не впливає на результат); у решті точок g(x) = 0.
не впливає на результат); у решті точок g(x) = 0.
Маємо:
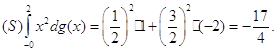
3) Обрахувати за формулою (15) інтеграли:
(а) ![]() , (б)
, (б) ![]() , (в)
, (в) ![]() ,
,
де 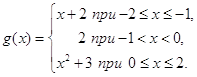
Розв’язок. Функція ![]() має скачки рівні 1, при
має скачки рівні 1, при ![]() і
і ![]() . Похідна
. Похідна
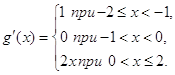
Тому
![]()
Аналогічно,
![]() і
і ![]()
3) Припустимо, що вздовж відрізку ![]() вісі х розташовані маси, як скупчені в окремих точках, так и розподілені неперервно. Не роблячи між ними відмінностей, позначимо для
вісі х розташовані маси, як скупчені в окремих точках, так и розподілені неперервно. Не роблячи між ними відмінностей, позначимо для ![]() через
через ![]() суму всіх мас, розташованих на проміжку
суму всіх мас, розташованих на проміжку ![]() ; більше того, покладемо
; більше того, покладемо ![]() =0. Очевидно,
=0. Очевидно, ![]() — монотонно зростаюча функція. Поставимо собі задачею знайти статичний момент цих мас відносно початку координат.
— монотонно зростаюча функція. Поставимо собі задачею знайти статичний момент цих мас відносно початку координат.
Розіб’ємо проміжок ![]() на частини точками
на частини точками
![]()
На відрізку ![]() при
при ![]() міститься, очевидно, маса
міститься, очевидно, маса![]() . Так само на відрізку
. Так само на відрізку ![]() міститься маса
міститься маса ![]() . Рахуючи масу в усіх випадках зосередженою, наприклад на правому кінці проміжку, отримаємо для шуканого статичного моменту наближений вираз
. Рахуючи масу в усіх випадках зосередженою, наприклад на правому кінці проміжку, отримаємо для шуканого статичного моменту наближений вираз
![]()
Коли всі ![]() прямують до 0, то у границі прийдемо до точкового результату:
прямують до 0, то у границі прийдемо до точкового результату:
![]() (16)
(16)
Можна було б і тут, спочатку встановити «елементарний» статичний момент ![]() що відповідає відрізку вісі від
що відповідає відрізку вісі від ![]() до
до ![]() а потім просумувати ці елементи.
а потім просумувати ці елементи.
Аналогічно для моменту інерції ![]() тих самих мас відносно початку знайдемо формулу
тих самих мас відносно початку знайдемо формулу
![]() (17)
(17)
Підкреслимо, що інтеграл Стілтъєса дав можливість об’єднати однією інтегральною формулою різнорідні випадки неперервно розподілених и зосереджених мас!
Нехай неперервно розподілені маси мають лінійну щільність ![]() ; окрім них, них у точках
; окрім них, них у точках ![]() розташовані зосереджені маси
розташовані зосереджені маси ![]() . Тоді, виключаючи ці точки, функція
. Тоді, виключаючи ці точки, функція ![]() має похідну
має похідну ![]() .
.
У кожній же точці ![]() функція має стрибок, рівний саме масі
функція має стрибок, рівний саме масі ![]() ,зосередженій в цій точці.
,зосередженій в цій точці.
Якщо тепер розкласти інтеграл (16) за формулою (15), то отримаємо
![]()
Придивившись до правої частини, у першому члені легко впізнати статичний момент неперервно розподілених мас, а в другому — статичний момент зосереджених мас. Аналогічний результат одержимо також для інтеграла (17).
 0
0
![]()
![]()
![]()
![]()
![]()
Рис.1
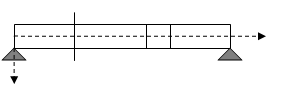
4) Розглянемо інше питання, в якому інтеграл Стілтьєса грає таку ж роль, як і у вправі 3). Припустимо, що на балку (рис. 1), що спирається на дві опори, окрім неперервно розподіленого навантаження діють і зосереджені сили. Розташуємо вісь х вздовж вісі балки, а вісь у вертикально донизу (див. рис. 1). Не будемо робити різниці між діючими силами, позначимо для ![]() через
через ![]() суму усіх сил, що прикладені на відрізку
суму усіх сил, що прикладені на відрізку ![]() балки, включаючи і реакції опір; далі, нехай
балки, включаючи і реакції опір; далі, нехай ![]() . Силу
. Силу ![]() називають перерізувальним зусиллям у перерізі
називають перерізувальним зусиллям у перерізі ![]() балки. При цьому сили, направлені донизу, будемо вважати додатними, а вгору — від’ємними.
балки. При цьому сили, направлені донизу, будемо вважати додатними, а вгору — від’ємними.
Поставимо завдання визначити так званий згинальний момент М у довільному перерізі ![]()
![]() | балки. Під цим розуміють суму моментів усіх сил, що діють на праву (або на ліву) частину балки, відносно цього перерізу. При цьому, коли мова іде про праву частину балки, момент вважають додатнім, якщо він обертає цю частину за годинниковою стрілкою (для лівої частини — обернене правило).
| балки. Під цим розуміють суму моментів усіх сил, що діють на праву (або на ліву) частину балки, відносно цього перерізу. При цьому, коли мова іде про праву частину балки, момент вважають додатнім, якщо він обертає цю частину за годинниковою стрілкою (для лівої частини — обернене правило).
Так як на елементі ![]() скажімо, правої частини балки прикладена силу
скажімо, правої частини балки прикладена силу ![]() що створює елементарний момент
що створює елементарний момент ![]()
то, «сумуючи», отримаємо
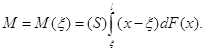
Аналогічно, виходячи з лівої частини балки, можна було б отримати (враховуючи зміну додатного напрямку для відліку моментів)
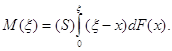 (18)
(18)
Легко безпосередньо побачити, що обидва вирази вигинального моменту дійсно тотожні. Їх рівність рівносильна умові ![]() яка є наслідком з умов рівноваги
яка є наслідком з умов рівноваги ![]() що виражає рівність нулю суми всіх сил і суми моментів (відносно початку) всіх сил, що діють на балку.
що виражає рівність нулю суми всіх сил і суми моментів (відносно початку) всіх сил, що діють на балку.
Якщо інтенсивність неперервно розподіленого навантаження позначити через ![]() то, виключаючи точки, де прикладені зосереджені сили, буде
то, виключаючи точки, де прикладені зосереджені сили, буде
![]()
Нехай зосереджені сили ![]()
![]() прикладені в точках
прикладені в точках ![]() . Тоді, очевидно, перерізаюче зусилля саме в цих точках має скачки, відповідно рівні
. Тоді, очевидно, перерізаюче зусилля саме в цих точках має скачки, відповідно рівні ![]() . Далі, застосовуючи, наприклад, до інтегралу (18) формулу (15), отримаємо
. Далі, застосовуючи, наприклад, до інтегралу (18) формулу (15), отримаємо
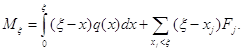
У двох доданках правої частини легко впізнати моменти, спричинені нарізно неперервним навантаженням і зосередженими силами: інтеграл Стілтъєса охоплює їх єдиною інтегральною формулою.
5) Формула (15) може бути корисна і для обрахунку звичайних інтегралів (у сенсі Рімана). Проілюструємо це наступним загальним прикладом.
Нехай ![]() - — «кусково-поліноміальна» функція на проміжку
- — «кусково-поліноміальна» функція на проміжку ![]() ; це означає, що проміжок розкладається на скінчене число частин точками
; це означає, що проміжок розкладається на скінчене число частин точками
![]()
так, що в кожній з частин функція ![]() представляється поліномом не вищим
представляється поліномом не вищим ![]() -го степеня. Замінивши значення функції
-го степеня. Замінивши значення функції ![]() і всіх її похідних у точках
і всіх її похідних у точках ![]() та
та ![]() нулями, позначимо через
нулями, позначимо через ![]() величину стрибка
величину стрибка ![]() -ї похідної
-ї похідної ![]() в
в ![]() -ій точці
-ій точці ![]()
Нехай, далі, ![]() — будь-яка неперервна функція; покладемо
— будь-яка неперервна функція; покладемо
![]() і, взагалі,
і, взагалі, ![]()
Тоді має місце наступна формула:
![]()
Дійсно, послідовно знаходимо
![]() ;
;
подвійна підстановка зникає, а інтеграл
![]() ;
;
аналогічно,
![]()
і т.д.
7) Встановимо, за допомогою формули (11) корисне узагальнення формули інтегрування за частинами для звичайних інтегралів. Саме якщо ![]() і
і ![]() обидві абсолютно інтегровні на проміжку
обидві абсолютно інтегровні на проміжку ![]() , a U(
, a U(![]() ) і V(
) і V(![]() ) визначаються інтегральними формулами:
) визначаються інтегральними формулами:
![]()
![]()
то справедлива формула
![]() (19)
(19)
Для доведення, за формулою (11) замінимо інтеграл зліва інтегралом Стілтьєса и проінтегруємо за частинами:
![]()
залишається ще раз застосувати формулу (11) до останнього інтегралу, щоб прийти до (19)
Тут функції ![]() грають як би роль похідних від функцій
грають як би роль похідних від функцій ![]() не будучи ними насправді. При неперервності функцій
не будучи ними насправді. При неперервності функцій ![]() і
і ![]() ми повертаємося до звичайної формули інтегрування за частинами, бо тоді
ми повертаємося до звичайної формули інтегрування за частинами, бо тоді
![]() ,
, ![]() . [2;7]
. [2;7]
§8. Граничний перехід під знаком інтеграла Стілтьєса
Теорема 1. Нехай функції ![]()
![]() неперервні на проміжку
неперервні на проміжку ![]() і при
і при ![]() рівномірно прямують до граничної функції
рівномірно прямують до граничної функції ![]() [очевидно, також неперервній], a
[очевидно, також неперервній], a ![]() — функція з обмеженою зміною. Тоді
— функція з обмеженою зміною. Тоді ![]()
Доведення. По заданому ![]() знайдеться таке
знайдеться таке ![]() , що при
, що при ![]() буде для всіх
буде для всіх ![]()
![]()
Тоді, в силу 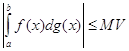 для
для ![]()
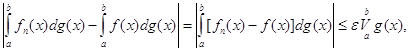
що, враховуючи довільність ![]() , і доводить теорему.
, і доводить теорему.
Теорема 2. Нехай тепер функція ![]() неперервна а проміжку
неперервна а проміжку ![]() , а функції
, а функції ![]()
![]() — всі з обмеженою зміною на цьому проміжку. Якщо повні зміни цих функцій в їх сукупності обмежені:
— всі з обмеженою зміною на цьому проміжку. Якщо повні зміни цих функцій в їх сукупності обмежені:
![]()
![]()
і ![]() при
при ![]() прямують до граничної функції
прямують до граничної функції
![]() , то
, то
![]()
Доведення. Перш за все впевнимося у тому, що гранична функція ![]() сама також буде мати обмежену зміну. Розкладемо проміжок
сама також буде мати обмежену зміну. Розкладемо проміжок ![]() довільним чином на частини точками
довільним чином на частини точками ![]() , будемо мати (при будь-якому
, будемо мати (при будь-якому ![]() )
) ![]()
Переходячи границі тут при ![]() , отримаємо
, отримаємо ![]() звідки і
звідки і ![]()
Складемо суми Стілтьєса ![]() ,
, ![]()
Якщо припустити, що проміжок ![]() при цьому розкладений на такі маленькі частини, що коливання функції
при цьому розкладений на такі маленькі частини, що коливання функції ![]() у кожній з них буде вже менше довільного наперед взятого числа
у кожній з них буде вже менше довільного наперед взятого числа ![]() , то, при всіх
, то, при всіх ![]()
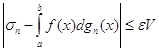 ,
, 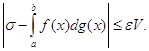 (27)
(27)
З іншого боку, якщо розбиття, обране під вказаною умовою фіксувати, то очевидно ![]() а при
а при ![]() , так що знайдеться таке
, так що знайдеться таке ![]() , що для
, що для ![]() буде
буде
![]() . (27)
. (27)
Тоді для тих самих значень ![]() будемо мати, в силу (27) і (28),
будемо мати, в силу (27) і (28),
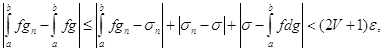
звідки, враховуючи довільність![]() , і випливає необхідний висновок. [1;7]
, і випливає необхідний висновок. [1;7]
Висновки
У даній роботі розглянуто означення і основні властивості інтеграла Стілтьєса, його зв’язок, особливості і відмінності від інших визначених інтегралів.
В ході виконання курсової роботи були з’ясовані загальні умови існування інтегралу Стілтьєса та 3 класи випадків його існування, а також вивчено порядок зведення інтегралу Стілтьєса до інтегралу Рімана.
У даній роботі досліджено 5 основних властивостей, подано метод граничного переходу під знаком інтегралу Стілтьєса та формула, за якою здійснюється інтегрування за частинами цього інтегралу.
Були розглянуті приклади застосування інтеграла Стілтьєса для розв’язку різних класів задач, зокрема, можливість об’єднання однією інтегральною формулою різнорідних випадків неперервно розподілених и зосереджених мас за допомогою інтеграла Стілтъєса.
Отже, слід зазначити, що інтеграл Стілтьєса має специфічні властивості і є не тільки узагальненням інтегралу Рімана, але й самостійним інструментом для розв’язку певного класу задач.
Список використаних джерел
1. Градштейн и Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений.- М.: Наука, 1963 – 312с.
2. Давидов М.О. Курс математчного анализу. Ч. 1. – К.:Вища школа, 1990. – 350с.
3. Канторович Л.В., Акитов Г.Л. Функциональный аналіз. – М.: ИЛ, 1961 – 321с.
4. Кудрявцев Л.Д. Курс математического анализа, т.2. - М.: Высшая школа, 1965. – 369с
5. Никольский С.М. Курс математического анализа - М.: Физматгиз, 2001 – 398с.
6. Макаров И.П. Дополнительные главы математического анализа: учебное поссобие. – М.: Прсвещение, 1968 - 307с.
7. Смирнов В.И. Курс высшей математики (В 5-ти т.) том 5. - М.-Л. АН СССР, 1959 – 452с.
8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (В 3-х томах) т.3. М.: Физматгиз, 1963 - 662с.
[1] Томас Іоанес Стілтьєс (нідерл. Thomas Joannes Stieltjes, 29.12.1856, — 31.12.1894 Тулуза) — нідерландський математик.
Запрпонував у 1894 р. узагальнення визначеного інтегралу (Інтеграл Рімана-Стілтьеса). Член-кореспондент Петербурзької Академії наук (1894).
0 комментариев