Навигация
Композиции зеркальной и центральной симметрий
25788
знаков
28
таблиц
10
изображений
1.3. Композиции зеркальной и центральной симметрий
Задача 7. Найти композицию зеркальной и центральной симметрий, если плоскость первой не содержит центр второй.
Решение. Пусть даны плоскость a и точка О, не принадлежащая ей. Найдем композицию ZO◦Sa. Центральная симметрия ZO как частный случай поворотной симметрии представима композицией осевой и зеркальной симметрии: ZO=Sl◦Sb, где l и b - перпендикулярные прямая и плоскость, причем lÇb=O. Выберем плоскость b таким образом, что a║b , тогда l будет являться перпендикуляром и к плоскости a (рис. 7). Тогда ZO◦Sa=Sl◦Sb◦Sa . В силу того, что плоскости a и b параллельны, их композиция есть параллельный перенос 
, при этом 
║l . А это по определению есть винтовое движение с осью l, углом 180°, вектором 
.
|
| O | |||||||||||||||||||||||
|
| L | A | h |
| ||||||||||||||||||||
| b | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
| l |
| |||||||||||||||||||||||
| A | ||||||||||||||||||||||||
| a | ||||||||||||||||||||||||
| l | a | O | ||||||||||||||||||||||
|
| ||||||||||||||||||||||||
| a | ||||||||||||||||||||||||
Рис. 7 Рис. 8
Итак, композиция зеркальной и центральной симметрий есть винтовое движение: ZO◦Sa= Sl◦. (3)
Задача 8. Найти композицию ZO◦Sa◦Sl , если прямая l параллельна плоскости a и точка О лежит в a.
Решение. На основании (3) композиция ZO◦Sa в общем случае есть винтовое движение. В силу того, что ОÎa, вектор винтового движения будет нулевым, и само винтовое движение выродится в осевую симметрию Sa , где a^a и OÎa (рис. 8). Тогда ZO◦Sa◦Sl=Sa◦Sl, причем a^l.
Если прямые a и l скрещиваются, то искомая композиция является винтовым движением Rhj◦
, угол j которого равен 2Ð(a, l)=p, ось h – общий перпендикуляр прямых a и l, вектор 
=2
, где L=lÇh, A=aÇh (см. [3], с. 19).
Если прямые a и l пересекаются, то =
, и композиция Sa◦Sl является осевой симметрией Sh, где h – это перпендикуляр к плоскости, проходящей через прямые a и l.
Похожие работы
... точка А сместилась в направлении f(l). Следовательно, в силу произвольности точки А, искомая трансформация есть косое сжатие с осью f(q), направлением f(l) и коэффициентом k. 17. Решение задач с помощью трансформации преобразований Задача 1. Даны правильные одинаково ориентированные треугольники OAB, OCD, OEF. Доказать, что середины M, N, P соответственно отрезков BC, DE, AF являются вершинами ...
... в сопряжённых комплексных координатах 1.1. Определение аффинного преобразования Введём определение аффинного преобразования евклидовой плоскости в сопряжённых комплексных координатах. Преобразование евклидовой плоскости называется аффинным, если оно отображает каждую прямую на прямую. [1] 1.2. Формула аффинного преобразования Мы хотим построить теорию аффинных преобразований с помощью ...
... вследствие объективных причин (болезнь детей) в эксперименте принимало участие 5 детей, проявлявших особый интерес к занятиям изобразительной деятельностью. Опытно - экспериментальную работу по развитию декоративного творчества детей старшего дошкольного возраста средствами декоративной композиции мы строили в три этапа: 1 - констатирующий эксперимент; 2 - формирующий эксперимент; 3 - итоговый ...
... идет о повороте в пространстве, надо учитывать, что = . В частности, = (отражение относительно прямой параллельной v и проходящей через О). Аналогично, = . Если при этом j = p это преобразование не зависит от вектора n и является отражением относительно точки О. 4* Композиции 1. Теорема 4 Если f и g два перемещения X, а f*, g* - соответствующие операторы в V, то (f· g)* = f*g*( ...
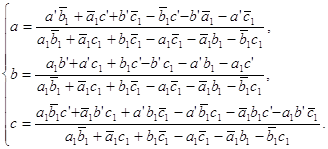
0 комментариев