Навигация
Тесноту связи оценим с помощью линейного коэффициента парной корреляции
2.1.2. Тесноту связи оценим с помощью линейного коэффициента парной корреляции.
Предварительно определим средние квадратические отклонения признаков.
Средние квадратические отклонения:
![]()
![]()
Коэффициент корреляции:
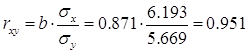
Между признаками X и Y наблюдается очень тесная линейная корреляционная связь.
2.1.3 Оценим качество построенной модели.
Определим коэффициент детерминации:
![]()
т. е. данная модель объясняет 90,5% общей дисперсии у, на долю необъясненной дисперсии приходится 9,5%.
Следовательно, качество модели высокое.
Найдем величину средней ошибки аппроксимации Аi .
Предварительно из уравнения регрессии определим теоретические значения ![]() для каждого значения фактора.
для каждого значения фактора.
Ошибка аппроксимации Аi, i=1…15:
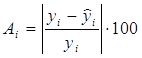
Средняя ошибка аппроксимации:
![]()
Ошибка небольшая, качество модели высокое.
5.1.4. Определим средний коэффициент эластичности:
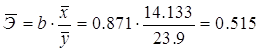
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0,515%.
2.1.5.Оценим статистическую значимость полученного уравнения. Проверим гипотезу H0, что выявленная зависимость у от х носит случайный характер, т. е. полученное уравнение статистически незначимо. Примем α=0,05. Найдем табличное (критическое) значение F-критерия Фишера:
![]()
Найдем фактическое значение F- критерия Фишера:
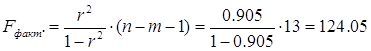
![]()
следовательно, гипотеза H0 отвергается, принимается альтернативная гипотеза H1: с вероятностью 1-α=0,95 полученное уравнение статистически значимо, связь между переменными x и y неслучайна.
Построим полученное уравнение.
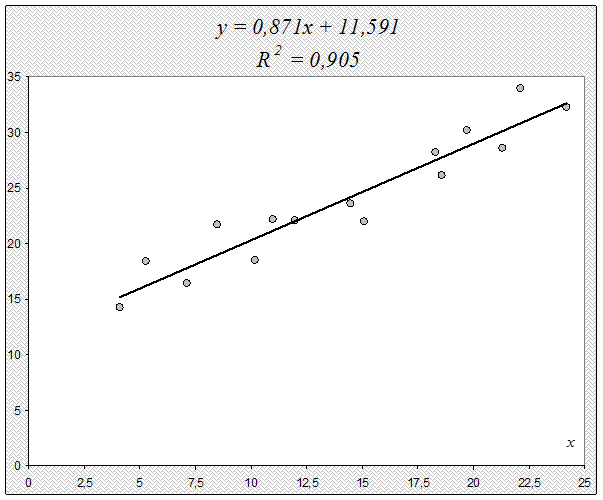
2.2. Модель полулогарифмической парной регрессии.
2.2.1. Рассчитаем параметры а и b в регрессии:
уx =а +blnх.
Линеаризуем данное уравнение, обозначив:
z=lnx.
Тогда:
y=a + bz.
Параметры a и b уравнения
![]() = a + bz
= a + bz
определяются методом наименьших квадратов:
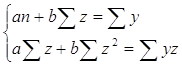 Рассчитываем таблицу 2.
Рассчитываем таблицу 2.
Таблица 2
| № | x | y | z | yz | z2 | y2 |
|
| Аi |
| 1 | 5,3 | 18,4 | 1,668 | 30,686 | 2,781 | 338,56 | 15,38 | 3,02 | 16,42 |
| 2 | 15,1 | 22,0 | 2,715 | 59,723 | 7,370 | 484,00 | 25,75 | -3,75 | 17,03 |
| 3 | 24,2 | 32,3 | 3,186 | 102,919 | 10,153 | 1043,29 | 30,42 | 1,88 | 5,83 |
| 4 | 7,1 | 16,4 | 1,960 | 32,146 | 3,842 | 268,96 | 18,27 | -1,87 | 11,42 |
| 5 | 11,0 | 22,2 | 2,398 | 53,233 | 5,750 | 492,84 | 22,61 | -0,41 | 1,84 |
| 6 | 8,5 | 21,7 | 2,140 | 46,439 | 4,580 | 470,89 | 20,06 | 1,64 | 7,58 |
| 7 | 14,5 | 23,6 | 2,674 | 63,110 | 7,151 | 556,96 | 25,34 | -1,74 | 7,39 |
| 8 | 10,2 | 18,5 | 2,322 | 42,964 | 5,393 | 342,25 | 21,86 | -3,36 | 18,17 |
| 9 | 18,6 | 26,1 | 2,923 | 76,295 | 8,545 | 681,21 | 27,81 | -1,71 | 6,55 |
| 10 | 19,7 | 30,2 | 2,981 | 90,015 | 8,884 | 912,04 | 28,38 | 1,82 | 6,03 |
| 11 | 21,3 | 28,6 | 3,059 | 87,479 | 9,356 | 817,96 | 29,15 | -0,55 | 1,93 |
| 12 | 22,1 | 34,0 | 3,096 | 105,250 | 9,583 | 1156,00 | 29,52 | 4,48 | 13,18 |
| 13 | 4,1 | 14,2 | 1,411 | 20,036 | 1,991 | 201,64 | 12,84 | 1,36 | 9,60 |
| 14 | 12,0 | 22,1 | 2,485 | 54,916 | 6,175 | 488,41 | 23,47 | -1,37 | 6,20 |
| 15 | 18,3 | 28,2 | 2,907 | 81,975 | 8,450 | 795,24 | 27,65 | 0,55 | 1,95 |
| Σ | 212,0 | 358,5 | 37,924 | 947,186 | 100,003 | 9050,25 | 358,50 | 0,00 | 131,14 |
| Средн. | 14,133 | 23,900 | 2,528 | 63,146 | 6,667 | 603,350 | 23,90 | 0,00 | 8,74 |
Разделив на n и решая методом Крамера, получаем формулу для определения b:
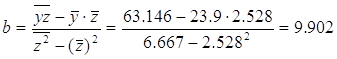
![]()
Уравнение регрессии:
![]() = -1,136 + 9,902z
= -1,136 + 9,902z
Похожие работы
... а также любые колебания, в которых прослеживается закономерность. В качестве примера можно назвать модель экспоненциального сглаживания Брауна. 3. Пример проведения прогнозирования прибыли с использованием пакета SPSS Постановка задачи: Необходимо построить модель, дающую возможность предсказывать размер прибыли некоторой торговой фирмы, если известны данные о ежемесячной прибыли за последние ...
... , и , то можно предположить о правильном распределении объектов и уже существующих двух классах и верно выполненной классификации объектов подмножества М0. 3.2 Пример решения задачи дискриминантным анализом в системе STATISTICA Исходя из данных по 10 странам (рис. 3.1), которые были выбраны и отнесены к соответствующим группам экспертным методом (по уровню медицинского обслуживания), ...
... ). В настоящее время в России начинают развертываться эконометрические исследования, в частности, начинается широкое преподавание этой дисциплины. Кратко рассмотрим в настоящей главе современную структуру эконометрики. Знакомство с ней необходимо для обоснованных суждений о возможностях применения эконометрических методов и моделей в экономических и технико-экономических исследованиях. 1.3. ...
... М.М. Анализ временных рядов и прогнозирование. М.: Финансы и статистика, 2001. 5. Джонстон Дж. Эконометрические методы. М.: Статистика, 1980. 6. Образцова О.Н., Назарова О.В., Канторович Г.Г. Экономическая статистика. Эконометрика. Методические материалы. – М.: ГУ – ВШЭ, 2000. 7. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 543 с. ...

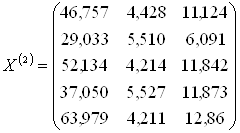
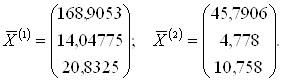
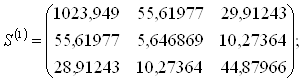
0 комментариев