Рассчитаем прогнозное значение результата у, если прогнозное значение фактора х увеличивается на 5% от его среднего уровня

5. Рассчитаем прогнозное значение результата у, если прогнозное значение фактора х увеличивается на 5% от его среднего уровня.

Точечный прогноз:

11,59+0,871,0514,13=24,515 млн. руб.

Для данной величины выпуска продукции прогнозное значение затрат на производство составляет 24,515 млн. руб.

Для уровня значимости α= 0,05 определим доверительный интервал прогноза.

Предварительно определим стандартные ошибки коэффициента корреляции и параметра b.

Стандартная ошибка коэффициента корреляции:

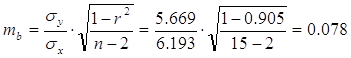
Ошибка прогноза:

Доверительный интервал прогноза значений y при  с вероятностью 0,95 составит:

Прогноз надежный, но не очень точный, т. к.

Задание 2

 

Имеются данные о заработной плате у (тысяч рублей), возрасте х₁ (лет), стаже работы по специальности х₂(лет) и выработке х₃ (штук в смену) по 15 рабочим цеха:

№	y	х1	х2	х3
1	3,2	30	6	12
2	4,5	41	18	20
3	3,3	37	11	12
4	3,0	33	9	18
5	2,8	24	4	15
6	3,9	44	19	17
7	3,7	37	18	17
8	4,2	39	22	26
9	4,7	49	30	26
10	4,4	48	24	22
11	2,9	29	8	18
12	3,7	31	6	20
13	2,4	26	5	10
14	4,5	47	19	20
15	2,6	29	4	15

Требуется:

1.   С помощью определителя матрицы парных коэффициентов межфакторной корреляции оценить мультиколлинеарность факторов, исключить из модели фактор, ответственный за мультиколлинеарность.

2.   Построить уравнение множественной регрессии в стандартизованной форме:

2.1.     Оценить параметры уравнения.

2.2.     Используя стандартизованные коэффициенты регрессии сравнить факторы по силе их воздействия на результат.

2.3.     Оценить тесноту связи между результатом и факторами с помощью коэффициента множественной корреляции.

2.4.     Оценить с помощью коэффициента множественной детерминации качество модели.

2.5.     Используя F-критерий Фишера оценить статистическую значимость присутствия каждого из факторов в уравнении регрессии.

3.   Построить уравнение множественной регрессии в естественной форме, пояснить экономический смысл параметров уравнения.

4.   Найти среднюю ошибку аппроксимации.

5.   Рассчитать прогнозное значение результата, если прогнозное значение факторов составит: х₁ = 35 лет, х₂ = 10 лет, х₃ = 20 штук в смену.

Решение.

Для оценки мультиколлинеарности факторов используем определитель матрицы парных коэффициентов корреляции между факторами.

Определим парные коэффициенты корреляции.

Для этого рассчитаем таблицу 7.

Используя рассчитанную таблицу, определяем дисперсию y, x₁, x₂, x₃.

Найдем среднее квадратическое отклонение признаков y, x₁, x₂, x₃, как корень квадратный из соответствующей дисперсии.

Определим парные коэффициенты корреляции:

 

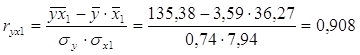
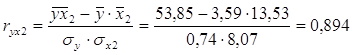
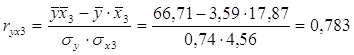
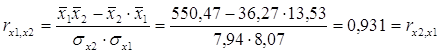
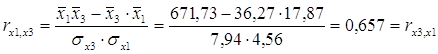
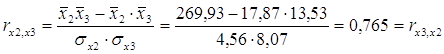
таблица 7

№	y	y2	x1	x12	x2	x22	x3	x32	yx1	yx2	yx3	x1x2	x1x3	x2x3			Аi
1	3,2	10,24	30	900	6	36	12	144	96,0	19,2	38,4	180	360	72	2,87	0,33	10,18
2	4,5	20,25	41	1681	18	324	20	400	184,5	81,0	90,0	738	820	360	4,00	0,50	11,03
3	3,3	10,89	37	1369	11	121	12	144	122,1	36,3	39,6	407	444	132	3,32	-0,02	0,73
4	3,0	9,00	33	1089	9	81	18	324	99,0	27,0	54,0	297	594	162	3,38	-0,38	12,79
5	2,8	7,84	24	576	4	16	15	225	67,2	11,2	42,0	96	360	60	2,65	0,15	5,47
6	3,9	15,21	44	1936	19	361	17	289	171,6	74,1	66,3	836	748	323	4,04	-0,14	3,54
7	3,7	13,69	37	1369	18	324	17	289	136,9	66,6	62,9	666	629	306	3,59	0,11	3,03
8	4,2	17,64	39	1521	22	484	26	676	163,8	92,4	109,2	858	1014	572	4,19	0,01	0,20
9	4,7	22,09	49	2401	30	900	26	676	230,3	141,0	122,2	1470	1274	780	4,83	-0,13	2,86
10	4,4	19,36	48	2304	24	576	22	484	211,2	105,6	96,8	1152	1056	528	4,56	-0,16	3,61
11	2,9	8,41	29	841	8	64	18	324	84,1	23,2	52,2	232	522	144	3,13	-0,23	7,82
12	3,7	13,69	31	961	6	36	20	400	114,7	22,2	74,0	186	620	120	3,36	0,34	9,17
13	2,4	5,76	26	676	5	25	10	100	62,4	12,0	24,0	130	260	50	2,51	-0,11	4,65
14	4,5	20,25	47	2209	19	361	20	400	211,5	85,5	90,0	893	940	380	4,39	0,11	2,46
15	2,6	6,76	29	841	4	16	15	225	75,4	10,4	39,0	116	435	60	2,97	-0,37	14,17
σ	53,8	201,08	544	20674	203	3725	268	5100	2030,7	807,7	1000,6	8257	10076	4049	53,80	0,00	91,69
ср.	3,59	13,41	36,27	1378,27	13,53	248,33	17,87	340,00	135,38	53,85	66,71	550,47	671,73	269,93	3,59	0,00	6,11

Матрица парных коэффициентов корреляции:

	y	x1	x2	x3
y	1,000
x1	0,908	1,000
x2	0,894	0,931	1,000
x3	0,783	0,657	0,765	1,000

Анализируем матрицу парных коэффициентов корреляции.

ú   r_x1x2=0.931, т. е. между факторами x₁ и x₂существует сильная корреляционная связь, один из этих факторов необходимо исключить.

ú   r_x1x3=0.657 меньше, чем r_x2x3=0.765, т.е. корреляция фактора х₂ с фактором х₃сильнее, чем корреляция факторов х₁ и х₃.

ú   Из модели следует исключить фактор х₂, т.к. он имеет наибольшую тесноту связи с х₃ и, к тому же, менее тесно (по сравнению с x₁) связан с результатом у (0.894<0.908).

2.1. Уравнение регрессии в естественной форме будет иметь вид:

 

y_x = a + b_lx_]+b₃x₃,

фактор х₂исключен из модели.

Стандартизованное уравнение:

 

t_y= β₁t_x1+β₃t_x3

где:

t_y, t_x1, t_x3 – стандартизованные переменные.

Параметры уравнения β₁ и β₃ определим методом наименьших квадратов из системы уравнений:

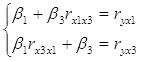
Или:

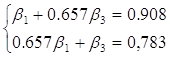
Систему решаем методом Крамера:

∆=	1	0,657	= 1-0,6572= 0,568
	0,657	1

∆β1=	0,908	0,657	= 0,908-0,6570,783=0,394
	0,783	1

∆β3=	1	0,571	=0,833-0,5710,413= 0,186
	0,413	0,833

Тогда:

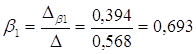
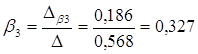
Получили уравнение множественной регрессии в стандартизованном масштабе:

t_y= 0,693t_x1+0,327t_x3

Коэффициенты β₁ и β₃ сравнимы между собой в отличии от коэффициентов чистой регрессии b₁ и b₃.

β₁=0,693 больше β₃=0,327, следовательно, фактор x₁ сильнее влияет на результат y чем фактор x₃.

Определим индекс множественной корреляции:

Cвязь между y и факторами x₁, x₃ характеризуется как тесная, т. к. значение индекса множественной корреляции близко к 1.

Коэффициент множественной детерминации:

R ²_yx1x3=(0.941)²=0.886

Т. е. данная модель объясняет 88,6% вариации y, на долю неучтенных в модели факторов приходится 100-88,6=11,4%

Оценим значимость полученного уравнения регрессии с помощью F-критерия Фишера:

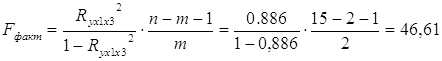
F_табл(α=0,05; k₁=2; k₂=15-2-1=12)=3,88

Табличное значение критерия Фишера (определяем по таблице значений критерия Фишера при заданном уровне значимости α и числе степеней свободы k₁ и k₂) меньше фактического значения критерия. следовательно, гипотезу H₀ о том, что полученное уравнение статистически незначимо и ненадежно, отвергаем и принимаем альтернативную гипотезу H₁: полученное уравнение статистически значимо, надежно и пригодно для анализа и прогноза.

Оценим статистическую значимость включения в модель факторов x₁ и x_2.

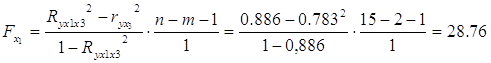
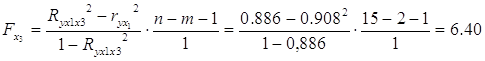
F_табл (α=0,05; k₁=1; k₂=15-2-1=12)=4,75

F_x1 >F_табл.

F_x3 >F_табл.

Значит, включение в модель факторов x₁ и x₃статистически значимо.

Перейдем к уравнению регрессии в естественном масштабе:

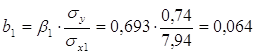
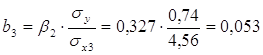
Уравнение множественной регрессии в естественном масштабе:

 

Экономическая интерпретация параметров уравнения:

b₁=0.064, это значит, что с увеличением x₁ – возраста рабочего на 1 год заработная плата рабочего увеличивается в среднем на 64 рубля, если при этом фактор x₂ - выработка рабочего не меняется и фиксирован на среднем уровне.

b₃=0,053, это значит, что с увеличением x₃ – выработки рабочего на 1 шт. в смену, заработная плата рабочего увеличивается в среднем на 53 рубля, если при этом фактор x₁ - возраст рабочего не меняется и фиксирован на среднем уровне.

a=0,313 не имеет экономической интерпретации, формально это значение результата y при нулевом значении факторов, но факторы могут и не иметь нулевого значения.

Найдем величину средней ошибки аппроксимации, таблица 7.

Ошибка аппроксимации А_i, i=1…15:

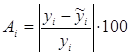
Средняя ошибка аппроксимации:

Ошибка небольшая, качество модели высокое.

Используем полученную модель для прогноза.

Если х₁ =35, х₂ =10, х₃ =20, то

у_р = 0,313 + 0,064•35 + 0,053•20 = 3,618 тыс. руб.

т. е. для рабочего данного цеха, возраст которого 35 лет, а выработка 20 шт. в смену, прогнозное значение заработной платы - 3618 руб.