Навигация
3. Выбор лучшего уравнения.
Составим таблицу полученных результатов исследования.
Таблица 4
| Уравнение | Коэффициент (индекс) корреляции | Коэффициент (индекс) детерминации | Средняя ошибка аппроксимации | Коэффициент эластичности |
| линейное | 0,951 | 0,905 | 6,65 | 0,515 |
| полулогагифмическое | 0,915 | 0,838 | 8,74 | 0,414 |
| степенное | 0,936 | 0,878 | 7,06 | 0,438 |
Анализируем таблицу и делаем выводы.
ú Все три уравнения оказались статистически значимыми и надежными, имеют близкий к 1 коэффициент (индекс) корреляции, высокий (близкий к 1) коэффициент (индекс) детерминации и ошибку аппроксимации в допустимых пределах.
ú При этом характеристики линейной модели указывают, что она несколько лучше полулогарифмической и степенной описывает связь между признаками x и у.
ú Поэтому в качестве уравнения регрессии выбираем линейную модель.
4. Для выбранной модели проверим предпосылку МНК о гомоскедастичности остатков, т. е. о том, что остатки регрессии имеют постоянную дисперсию.
Используем метод Гольдфельдта-Квандта.
1. Упорядочим наблюдения по мере возрастания переменной х.
2. Исключим из рассмотрения 3 центральных наблюдения.
3. Рассмотрим первую группу наблюдений (малые значения фактора х) и определим ![]() этой группы.
этой группы.
4. Рассмотрим вторую группу наблюдений (большие значения фактора х) и определим ![]() этой группы.
этой группы.
5. Проверим, значимо или незначимо отличаются дисперсии остатков этих групп.
Таблица 5
| № | x | y | yx | x2 | y2 |
|
|
|
| 1 | 4,1 | 14,2 | 58,22 | 16,81 | 201,64 | 15,47 | -1,27 | 1,60 |
| 2 | 5,3 | 18,4 | 97,52 | 28,09 | 338,56 | 16,50 | 1,90 | 3,61 |
| 3 | 7,1 | 16,4 | 116,44 | 50,41 | 268,96 | 18,05 | -1,65 | 2,72 |
| 4 | 8,5 | 21,7 | 184,45 | 72,25 | 470,89 | 19,26 | 2,44 | 5,97 |
| 5 | 10,2 | 18,5 | 188,70 | 104,04 | 342,25 | 20,72 | -2,22 | 4,93 |
| 6 | 11,0 | 22,2 | 244,20 | 121,00 | 492,84 | 21,41 | 0,79 | 0,63 |
| сумма | 46,2 | 111,4 | 889,53 | 392,60 | 2115,14 | 111,40 | 0,00 | 19,46 |
| среднее | 7,70 | 18,57 | 148,26 | 65,43 | 352,52 | 18,57 | 0,00 | 3,89 |
Определим параметры уравнения регрессии 1 группы:
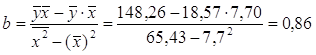
![]()
Уравнение регрессии 1 группы:
![]() =11,93+0,86x
=11,93+0,86x
Таблица 6
| № | x | y | yx | x2 | y2 |
|
|
|
| 10 | 18,3 | 28,2 | 516,06 | 334,89 | 795,24 | 27,56 | 0,64 | 0,41 |
| 11 | 18,6 | 26,1 | 485,46 | 345,96 | 681,21 | 27,85 | -1,75 | 3,06 |
| 12 | 19,7 | 30,2 | 594,94 | 388,09 | 912,04 | 28,92 | 1,28 | 1,63 |
| 13 | 21,3 | 28,6 | 609,18 | 453,69 | 817,96 | 30,49 | -1,89 | 3,56 |
| 14 | 22,1 | 34,0 | 751,40 | 488,41 | 1156,00 | 31,27 | 2,73 | 7,47 |
| 15 | 24,2 | 32,3 | 781,66 | 585,64 | 1043,29 | 33,32 | -1,02 | 1,03 |
| сумма | 124,2 | 179,4 | 3738,70 | 2596,68 | 5405,74 | 179,40 | 0,00 | 17,17 |
| среднее | 20,70 | 29,90 | 623,12 | 432,78 | 900,96 | 29,90 | 0,00 | 3,43 |
Параметры уравнения регрессии 2 группы:
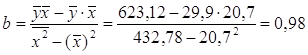
![]()
Уравнение регрессии 2 группы:
![]() =9,7+0,98x
=9,7+0,98x
S1=19.46>S2=17.17
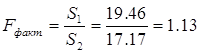
![]()
Fфакт.< Fтабл.
следовательно, остатки гомоскедастичны, предпосылки МНК не нарушены.
Похожие работы
... а также любые колебания, в которых прослеживается закономерность. В качестве примера можно назвать модель экспоненциального сглаживания Брауна. 3. Пример проведения прогнозирования прибыли с использованием пакета SPSS Постановка задачи: Необходимо построить модель, дающую возможность предсказывать размер прибыли некоторой торговой фирмы, если известны данные о ежемесячной прибыли за последние ...
... , и , то можно предположить о правильном распределении объектов и уже существующих двух классах и верно выполненной классификации объектов подмножества М0. 3.2 Пример решения задачи дискриминантным анализом в системе STATISTICA Исходя из данных по 10 странам (рис. 3.1), которые были выбраны и отнесены к соответствующим группам экспертным методом (по уровню медицинского обслуживания), ...
... ). В настоящее время в России начинают развертываться эконометрические исследования, в частности, начинается широкое преподавание этой дисциплины. Кратко рассмотрим в настоящей главе современную структуру эконометрики. Знакомство с ней необходимо для обоснованных суждений о возможностях применения эконометрических методов и моделей в экономических и технико-экономических исследованиях. 1.3. ...
... М.М. Анализ временных рядов и прогнозирование. М.: Финансы и статистика, 2001. 5. Джонстон Дж. Эконометрические методы. М.: Статистика, 1980. 6. Образцова О.Н., Назарова О.В., Канторович Г.Г. Экономическая статистика. Эконометрика. Методические материалы. – М.: ГУ – ВШЭ, 2000. 7. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 543 с. ...

0 комментариев