Модель повинна бути правильно специфікованою

5. Модель повинна бути правильно специфікованою.

6. Випадкова величина  відповідає нормальному закону розподілу з нульовим математичним сподіванням і постійною дисперсією.

7. Відсутність мультиколінеарності між факторами х, тобто фактори повинні бути незалежними між собою. Не повинно бути лінійного зв’язку між двома або більше факторами.

При побудові моделей регресії можна зіткнутися з проблемою мультиколінеарності, під якою розуміється тісна залежність між факторними ознаками, включеними в модель. Мультиколінеарність істотно змінює результати дослідження.

Одним з індикаторів визначення наявності мультиколінеарності між факторними ознаками є перевищення величини парного коефіцієнта кореляції 0,8 ().

Усунення мультиколінеарності може реалізовуватися через виключення з кореляційної моделі одного чи декількох лінійно зв'язаних факторних ознак у нові, укрупнені фактори [8, 19].

Розглянемо проблему мультиколінеарності детальніше. Припустимо, що є лінійна залежність  та . В такому випадку неможливо точно визначити окремий вплив кожного з цих факторів на залежні змінну у. Математично відсутність колінеарності між двома факторами визначається так, що не існує таких чисел  та , які одночасно не дорівнюють 0, для яких би існувала тотожність:

, (2.1.8)

Отже приймаємо, що коли між двома змінними є лінійний зв‘язок, то йдеться не про дві, а про одну незалежну змінну, бо неможливо знайти окремий вплив кожної з цих змінних на у.

Розглянемо етапи побудови багатофакторної регресійної моделі. Процес побудови багатофакторної регресійної моделі більш складний, ніж процес побудови простої лінійної регресії та складається з багатьох етапів:

1.   Вибір та аналіз усіх можливих факторів, які впливають на процес (або показник), що вивчається;

2.   Вимір та аналіз знайдених факторів;

3.   Математико-статистичний аналіз факторів.

4.   Вибір методу побудови регресійної багатофакторної моделі;

5.   Оцінка невідомих параметрів регресійної моделі;

6.   Перевірка моделі на адекватність;

7.   Розрахунок основних характеристик та побудова інтервалів довіри;

8.   Аналіз отриманих результатів, висновки.

На першому етапі дослідник повинен глибоко зрозуміти сам економічний процес, розглянути його з мікроекономічних та макроекономічних позицій, виявити якомога більше факторів, які в конкретному випадку можуть справити суттєвий або несуттєвий вплив на його зміну.

На етапі кількісного аналізу необхідно оцінити можливість кількісного вираження відібраних факторів, провести вимірювання та зібрати статистику для кількісних факторів, підібрати або створити балову шкалу оцінок якісних даних. З подальшого розгляду вилучаються також фактори, за якими немає або недоступна статистика.

Етап математик-статистичного аналізу є найважливішим підготовчим етапом для побудови регресійної багатофакторної моделі. Це заключний етап формування необхідної інформаційної бази. При наявності у динамічних рядах недостатньої інформації саме на цьому етапі за допомогою спеціальних методів проводиться її відтворення. На цьому етапі проводиться перевірка основних припущень класичного регресійного аналізу, крім того, здійснюється найважливіша процедура багатофакторного аналізу – перевірка факторів на мультиколінеарність. Для цього будується матриця коефіцієнтів парної кореляції, яка є симетричною. Потім аналізуються коефіцієнти парної кореляції між факторами. Якщо значення деяких з них близьке до 1, то це вказує на щільний зв’язок між ними, або на мультиколінеарність. Тоді один з факторів треба залишити, а інший вилучається з подальшого розгляду. Найчастіше залишають той фактор, який з економічної точки зору біль вагомий для аналізу впливу на залежну змінну. Або можна залишити фактор, що має більший коефіцієнт із залежною змінною у. Такий аналіз проводиться для кожної пари залежних між собою факторів. Результатом етапу математико-статистичного аналізу є знаходження множини основних незалежних між собою факторів, які є базою для побудови регресійної моделі.

Метод побудови регресійної багатофакторної моделі неможливо відокремити від самої моделі, вони найщільнішим чином пов’язані між собою. Саме обраний метод впливає на остаточний вигляд регресійної моделі.

Далі розраховуються невідомі параметри багатофакторної регресії за методом найменших квадратів. Нехай існує ряд спостережень за залежною змінною  та за незалежними змінними, або факторами:

.

На підставі цих спостережень будується лінійна вибіркова багатофакторна модель, а саме:

, (2.1.9)

де y – залежна змінна;

 - незалежні змінні (фактори);

 - невідомі параметри;

 - випадкова величина.

Сутність методів найменших квадратів полягає у потребі мінімізувати суму квадратів відхилень фактичних даних від теоретичних:

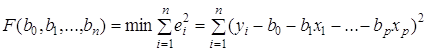, (2.1.10)

Для того, щоб знайти мінімум цього виразу, необхідно прирівняти до нуля часткові похідні функції F за аргументами . Отримаємо систему нормальних рівнянь.

Розглянемо властивості методу найменших квадратів:

1. Багатофакторна регресійна модель правильна для середніх точок . Тобто для моделі

 (2.1.11)

маємо: .

2. Середнє значення оцінки дорівнює середньому значенню фактичних даних, тобто . Це виходить з простого перетворення:

 (2.1.12)

,

Просумуємо обидві частини рівняння за , а також виходячи з того, що 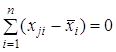; для , отримаємо .

Для спрощення пояснення наступних властивостей введемо умовні позначення. Позначимо , тоді рівність (2.1.12) можна записати так:

, (2.1.13)

де.

Тому багатофакторну вибіркову модель можна записати у формі:

, (2.1.14)