Факторные модели ДП

2.4.2 Факторные модели ДП

В этом случае ДП представляют в виде "черного ящика" (рисунок 2.13), электрические параметры которого определяет система уравнений. Каждое из уравнений, выбранной системы, выражает зависимость выходного электрического от соответствующего фактора. В качестве выходного параметра, как правило, выбирают полную проводимость. Тогда уравнение можно записать в виде

Y = (X), (2.38)

где Y- полная проводимость ДП;

Х= [Xl,X2,...,Xi,...,Xn]-вектор факторов;.

п - количество факторов.

Факторами могут служить частота f, напряжение U или ток I смещения рабочей точки, температура Т окружающей среды и т .п.

Из анализа факторной модели ДП представленной формулой (2.38) следует:

- ее рациональность - при включения в электрическую схему добавляют всего один всего один узел;

- возможность определять работоспособность ДК по выходным параметрам в процессе их экспериментального определения.

Таким образом, в практической электронике, связанной с проектированием РЭС, преимущества факторной модели очевидны. С другой стороны, по параметрам факторной модели всегда можно определить компонентную модель.

2.5 Модели МП

2.5.1 Традиционные способы описания параметров МП

Описание моделей, как правило, производят с помощью эквивалентных схем - компонентная модель, с помощь матрицы - формальная модель.

Компонентную модель формируют на основе линейных и нелинейных ДП. Такие модели целесообразны для описания активных элементов, например транзисторов, когда применяемые в модели ДП имеют чисто физический смысл.

Формальная модель представляет собой матрицу коэффициентов, которая определяет связь между входными и выходными параметрами МП: токами и напряжениями или падающими и отраженными волнами. Для моделирования МП применяют матрицы Y проводимости, Z сопротивления, А передачи, Н гибридную, S волновую матрицу рассеяния, Т волновую матрицу передачи. Для всех входных и выходных параметров используют следующие матричные уравнения:

I = Y U ; U = Z 1; hi - A d2: hi = Н h2; b = S a: a = Т b, (2.39)

где I = [ Il,...,Ii,...,In ] - вектор столбец токов:

U= [ Ul,...,Ui,...,Un ] - вектор столбец напряжений;

hl= [ U 1,12] - вектор столбец входных параметров;

h2= [ 11 ,U2] - вектор столбец входных параметров;

dl= fUl,Il] - вектор столбец входных параметров;

d2= [ЧЛД1] - вектор столбец входных параметров;

а = [ al,... ,ai,... ,ап]- вектор столбец падающих волн;

b = [ ] - вектор столбец отраженных волн.

i - текущий индекс параметра;

п - размер матрицы.

Все матрицы можно пересчитать из одной в другую при одинаковых их размерах. На практике наиболее часто при анализе МП применяют Y-, Z- , S- и Т-матрицы, а при анализе четырехполюсников, кроме перечисленных, гибридные. А- и Н-матрицы.

Рассмотрим свойства этих матриц. Линейные динамические параметры многополюсника выражают связь токов и напряжений, которые вырабатываются на его входах-полюсах при подключении их к внешним электрическим цепям. Рассмотрим многополюсник (рисунок 2.13) с числом полюсов п, в котором определены токи Ij и напряжение Uj для каждого i-ro входа. Напряжения Uj приложены между зажимами 1-го входа, один из которых представляет общую для входов-полюсов шину. Все токи Ij направлены к многополюснику, а напряжения U_s - от активного зажима к общей нулевой шине.

Пусть совокупность полюсных токов представляет вектор столбец I полюсных токов, а совокупность полюсных напряжений - вектор столбец U полюсных напряжений

I=P_r..,L,...I_n]^T, (2.40)

U=[U₁,...,U_i,...U_n]^T. (2.41)

Если считать Uj значения элементов вектора U заданными, значения Ij элемен­тов вектора I искомыми, то Ii можно рассматривать как линейную комбинацию U_bU2,-, U_n, т.е.

Тогда компоненты вектора I могут быть выражены в виде системы уравнений

I = YU, (2.45)

где Y - матрица проводимостей.

F

Если теперь считать Ij заданными величинами, а Ц искомыми, то по тем же соображениям U; значение вектора U можно рассматривать как линейную комбина­цию 1_Ь I₂,...,In, т.е.

Из уравнения (2.46) после несложных рассуждений приходим к матричному уравнению, связывающему компоненты векторов U и I в виде:

U = Z-I, (2.47)

где Z - матрица сопротивлений по форме аналогичная матрице Y.

В САПР электронных схем матрицы Y радиокомпонентов или отдельных схем имеют исключительное значение, так как содержат информацию для расчета электрических схем общепринятым методом узловых потенциалов.

Матрицы Z используются для расчета цепей методом контурных токов. Они находят меньшее применение. Матрицы Y и Z связаны друг с другом уравнением

Y - Z"¹, (2.48)

где -1 - знак обращения матрицы..

Y и Z - матрицы РК могут быть определены по параметрам эквивалентных схем или путем непосредственного их измерения.

Прямой метод определения Y - матриц производят путем измерения их коэффициентов при реализации опытов короткого замыкания полюсов. Для этого, например, к полюсу i прикладывают напряжение Ц, а остальные полюсы замыкают попарно с общей шиной. Поэтому все напряжения Uj при j i будут равны нулю, а система уравнений (2.46) трансформируется к виду:

Из системы уравнений (2.49) вытекает, что диагональный элемент уц будет определен в виде

Из уравнения (2.50) также следует, что диагональные у и коэффициенты матрицы Y представляют собой входную проводимость многополюсника со стороны полюса i при коротком замыкании остальных полюсов (рисунок 2.14). Таким образом, коэффициент у_н может быть определен с помощью измерителя полных проводимостей без каких-либо существенных трудностей.

Из формулы (2.51) также видно, что для определения недиагонального коэффициента Y - матрицы необходимо измерить модуль и фазу переменного тока очередного полюса], который коротко замкнут. Высокочастотные измерители модуля и фазы переменного тока промышленностью не выпускаются. Идентификация таких токов с помощью активных сопротивлений путем измерения модуля и разности фаз переменного напряжения, выделяющегося на этом сопротивлении, не позволяет полностью реализовать опыт короткого замыкания и тем самым приводит к нарушению условий эксперимента.

С другой стороны, в ряде случаев опыты короткого замыкания на выходах реальных многополюсных компонентов могут также привести к искажениям, например, из-за того, что при коротком замыкании выходного полюса режим измеряемого РК принудительно нарушается или вообще не допустим.

Попытка получить более удовлетворительные результаты путем реализации процесса измерения элементов Z-матриц при опытах холостого хода с последующим расчетом Y-матриц по формуле (2.48) нереальна, т.к. в этом случае при измерении на высоких частотах будет существенно проявляться шунтирующее действие входных цепей измерительного прибора, а также в некоторых случаях - цепей электропитания по постоянному току.

В режиме холостого хода многополюсник на рисунке 2.14 преобразуется в многополюсник, показанный на рисунке 2.15.

В режиме холостого хода все токи Ij при j=i, будут равны нулю, а развернутая система уравнений (2.49) трансформируется к виду

u.i-z..l,

1 hi

и. =z..i..

i и i

(2-52)

u. = z..i.

j ji i

U = z L.

n m i

Из системы уравнений (2.52) непосредственно получаем формулы для расчета диагональных элементов Z - матрицы

Из формул (2.53) и (2.54) видно, что диагональные zh коэффициенты Z - матрицы представляют собой входное сопротивление многополюсника со стороны полюса i при холостом ходе остальных полюсов (рисунок 2.15). Этот коэффициент может быть определен с помощью измерителя полных сопротивлений. Однако определение недиагональных Zjj коэффициентов на высоких частотах проблематично, во-первых, из-за сложности определения тока I;, во-вторых, из-за неизбежного искажения информации при измерении напряжений Ц при j i, которое возникает из-за шунтирующего действия входной цепи измерительного прибора.

Кроме того, в реальных устройствах режим холостого хода, во-первых, не используется и, во-вторых, может быть не реализуемым, например, из-за возникновения самовозбуждения измеряемого многополюсника (для активных многополюсников).

Рассмотрим определение матриц рассеяния. Физической основой S-параметров являются энергетические отношения между многополюсником и устройствами, подключенными к его входам-полюсам [2, 4]. S-параметры многополюсника позволяют определить обмен энергией между многополюсником, источниками энергии и нагрузками, подключенными к его входам. Аналитическое описание процессов производится посредством векторов падающих а волн, направленных к многополюснику, и отраженных b волн, направленных от него (рисунок 2.16). Волны а и b нормированы таким образом, чтобы выполнялся принцип инвариантности мощности. Поэтому размерность каждой из составляющих векторов а и b выражается в виде корня квадратного уравнения из мощности - (Вт)'^/2 . Связь между векторами а и b определяется матрицей рассеяния S, причем матричное уравнение имеет вид

b = Sa . (2.55)

Для линейных активных и пассивных многополюсников существует однозначная аналитическая связь между S-матрицей и матрицами проводимости Y, сопротивления Z и гибридными матрицами. Элементы матриц Y,Z,H, рассчитанные через S-матрицу должны быть при этом также нормированы. В важном для практики случае нормированная Y — матрица связывает вектор нормированных токов I с вектором нормированных напряжений U^H.

Чтобы сохранить принцип инвариантности мощности размерность составляющих векторов U^H и 1^Н должна отвечать корню квадратному из мощности, что достигается выбором в качестве нормирующего множителя сопротивления определенной величины. Это сопротивление в реальных условиях моделирует или волновое сопротивление линии передачи, подключаемой к i-тому полюсу или же номинал резистивной нагрузки этого же полюса. В общем случае выбор значения нормирующего сопротивления произволен[43]. На практике значение нормирующего сопротивления ri для i-полюса выбирают так, чтобы осуществлялся режим передачи наибольшей мощности от источников энергии к многополюснику и от многополюсника к нагрузкам, моделируемых резисторами номиналом rj (режим согласования). Соблюдая принцип инвариантности мощности, нормированные токи и напряжения на входах-полюсах многополюсника вычисляем по правилам

Компоненты векторов а, Ь, 1(1) и U^H(U) в общем случае имеют комплексный характер.

Чтобы адекватно установить связь между нормированными S- и Y-матрицами, необходимо выполнить условия

Уравнения (2.62) и (2.63) имеют важное значение, так как они позволяют, если это возможно, по результатам измерения абсолютных значений комплексных токов и напряжений I_s и Ц вычислить необходимые для определения коэффициентов S-матрицы значения нормированных волн ai и bj.

Матричное уравнение связи векторов I и U имеет вид [3]

I - YU, (2.64)

где Y - матрица проводимости многополюсника.

Решая уравнение (2.64), для нормированных векторов I и U относительно векторов а и b с учетом уравнений (2.58) - (2.63), после несложных преобразований получаем матричное уравнение, определяющее зависимость между нормированной матрицей проводимости Y^H и матрицей рассеяния S

Y^H = (1-S)(1 +S)*, (2.65)

где 1 - единичная матрица.

Таким образом, матрицу Y^H можно вычислить по известной S - матрице, коэффициенты которой можно определить по результатам измерения токов и напряжений на входах многополюсника, предварительно вычислив значения падающих и отраженных волн по формулам (2.63) и (2.64).

Основное преимущество идентификации матрицы Y^H по известной матрице S заключается в том, что определение информации, необходимой для идентификации коэффициентов S матрицы может быть произведено при подключении к входам многополюсника активных конечных или комплексных реактивных нагрузок [4, 2, 36, 48], тогда как способы экспериментального определения коэффициентов матри­цы Y , связанные с реализацией опытов короткого замыкания, которые, например, при измерении активных МП, выполнить сложно или вообще невозможно. Кроме того, при прямых способах измерения коэффициентов Y-матрицы необходимо определять значения токов и значения напряжений на входах многополюсника, тогда как осуществить измерение токов на высоких и сверхвысоких частотах практически невозможно.

Методика измерений, широко используемая при идентификации коэф­фициентов S-матриц СВЧ устройств [4] предусматривает следующие действия. МП включают в согласованный СВЧ тракт, идеальный СВЧ тракт, в котором отсутствуют или практически несущественны, отражения волн от согласованных нагрузок и источников сигналов. Разделение волн на падающие и отраженные с целью определения их значений производится с помощью устройств типа направленных ответвителей энергии.

Эквивалентная схема измерительной цепи для случая без применения устройств разделения падающих и отраженных волн может быть сведена к схеме, показанному на рисунке 2.17. Сущность методика измерения коэффициентов S-матрицы вытекает из анализа развернутой формы матричного уравнения (2.49) относительно входов исследуемого многополюсника i и j

Так как для случая рисунка 2.17 все падающие волны aj (j^i) равны нулю ввиду того, что все волны bj (j=Јi) поглощаются нагрузочными резисторами, то уравнение (2.69) можно записать в виде

Из уравнения (2.67) непосредственно находим выражения для определения 8„ диагональных и Sjj недиагональных коэффициентов S-матрицы

Из уравнений (2.58) устанавливаем, что для определения коэффициентов S-матрицы достаточно знать только отношение значений падающих и отраженных волн, что является основным преимуществом метода.

На более низких, чем СВЧ, частотах применить устройства, позволяющие разделить падающие и отраженные волны, практически не представляется возможным. Поэтому имеется потребность модификации методики измерения.

Гибридные, а именно Н-параметры, также являются системными параметрами и могут быть рассчитаны по известным Y- или Z-матрицам. Наиболее широкое применение получили Н-параметры транзисторов, представляемых в виде четырехполюсников [5]. Коэффициенты Н-матрицы определяют при холостом ходе на его входе и коротком замыкании на его выходе.

Похожие работы

Совершенствование организации управленческого труда в организации

Скачать

128462

1

16

... приведен полный перечень и расчетные формулы используемых для оценки ТК РЭА количественных показателей. 3.2 Разработка информационного обеспечения системы показателей эффективной организации управленческого труда в организации и технологичности конструкции изделий и их составных частей Стандартами ЕСТПП введена система количественных оценок технологичности конструкций, охватывающая всю ...

Поисково-разведочные работы. Восточные Саяны

Скачать

95619

8

4

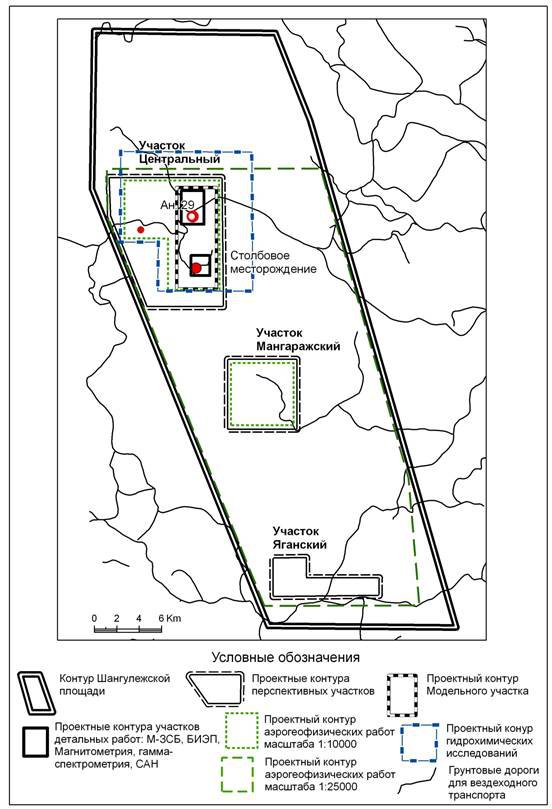
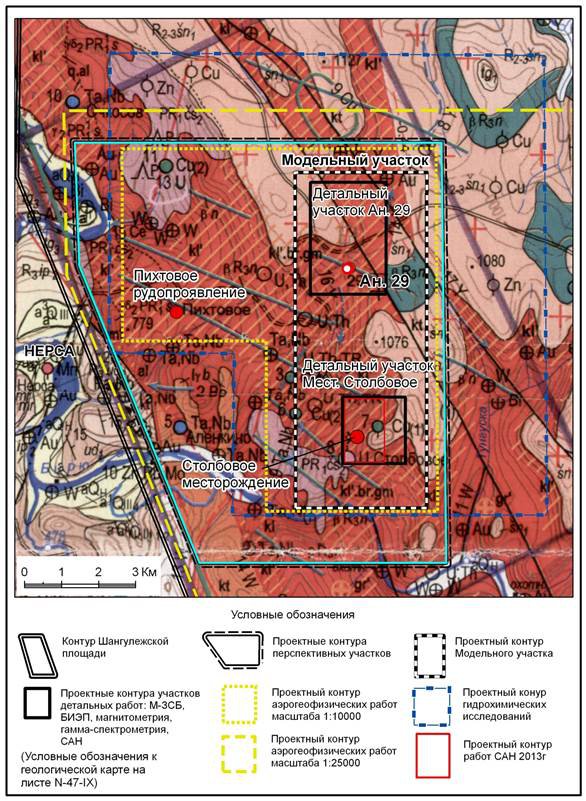
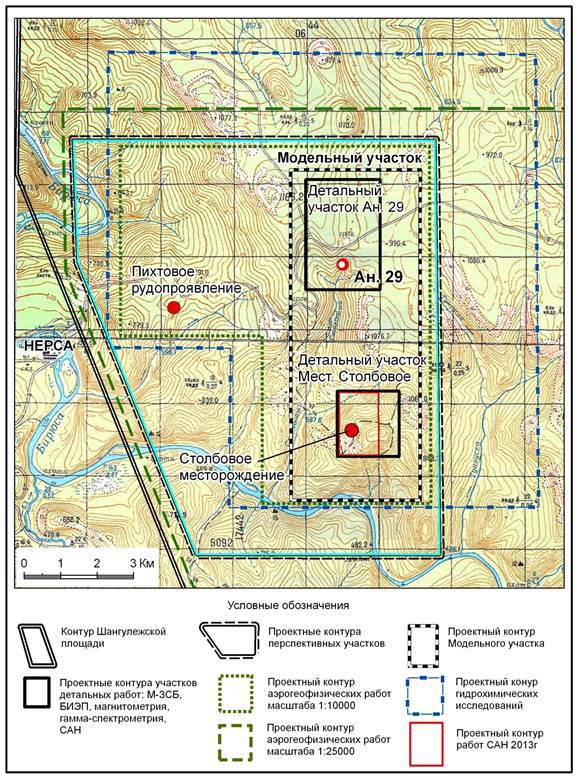
... (кимберлиты, лампроиты) и сопровождающихся процессами брекчирования, катаклаза, милонитизации и метасоматоза. Наиболее крупные глубинные разломы, прослеживающиеся на Шангулежской площади - Присаянский глубинный разлом, отделяющий структуру Восточного Саяна от Сибирской платформы, и субпараллельный ему Очкосовский, осложняющий восточную границу Бирюсинского купола. 4.2 Ураноностность площади. В ...

Концепция системы управления РУПП "Витязь"

Скачать

81636

14

5

... в соответствии со складывающейся ситуацией, изменение маркетинговой политики, разработка и реализация программ по увеличению продаж. 2. ПРЕДЛОЖЕНИЯ ПО ФОРМИРОВАНИЮ СИСТЕМЫ УПРАВЛЕНИЯ 2.1 Определение миссии РУПП «Витязь»   Миссия РУПП «Витязь» - обеспечение потребителей высококачественной продукцией, как телевизионной и спутниковой техникой, так и медицинской техникой, а также другими ...

Интеллектуальные датчики

Скачать

123695

1

3

... ИД состоит в выполнении им, помимо основной функции, функции автоматического метрологического самоконтроля - контроля метрологической исправности. Для повышения эффективности проектирования интеллектуальных датчиков необходимо создание баз данных, касающихся: 1. физических и химических процессов в чувствительных элементах датчиков, порождающих рост опасных составляющих погрешности; 2. динамики ...