Навигация
1.3 Критерій Баєса-Лапласа
Один із відомих класичних критеріїв прийняття рішень являється Критерій Байєса – Лапласа. Критерій Байєса – Лапласа враховує кожне з можливих наслідків всіх варіантів рішень:
![]()
Відповідне правило вибору можна інтерпретувати таким чином: матриця рішень [Wіj] доповнюється ще одним стовпцем, що містить математичне очікування значень кожного з рядків. Вибирається той варіант, в рядках якого коштує найбільше значення Wіj цього стовпця.
Критерій Байєса – Лапласа пред'являє до ситуації, в якій ухвалюється рішення, наступні вимоги:
ймовірність появи стану Vj відома і не залежить від часу;
ухвалене рішення теоретично допускає нескінченно велике
кількість реалізацій;
допускається деякий ризик при малих числах реалізацій.
Критерій Байєса – Лапласа може бути застосовуватись тільки в тому випадку, коли відомі ймовірності реалізації умов. [З]
Також зазначу пару слів про експоненційний метод розподілу, за яким формуємо матрицю рішень згідно завдання.
Вектори використовуються для опису функціонування систем, в яких перевищена кількість подій відбувається за відносно короткий проміжок часу, а окремі події для своєї реалізації потребують значно довших часових відтінків, наприклад час обслуговування клієнтів у банку, надходження автомобілів на заправну станцію, термін придатності електронних складових побутових пристроїв та ін.
Коли ймовірність появи події в малому інтервалі часу дуже мала і не залежить від появи інших подій, то інтервали часу між послідовними подіями розподіляються за експоненціальним законом.
Експоненціальний розподіл:
![]()
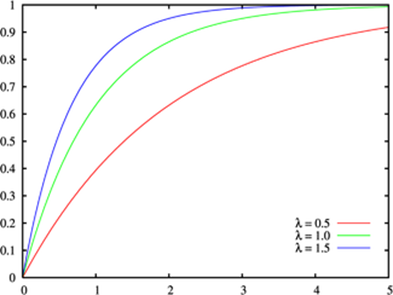
Рисунок 1 – Графік експоненціального закону розподілу
Цьому закону розподілу підлягає багато явищ, наприклад тривалість телефонних розмов, строк служби електронних деталей, час прибуття літака в аеропорт та ін. [4]
Розділ 2. Математичний опис
Приклад №1:
Розглянемо задачу ПР із 6 альтернативами із 8 можливими станами.
Задано матриці U(х,s) – станів і р(х,s) – ймовірностей, значення яких подані в таблиці 1 і таблиці 2 відповідно:
Таблиця 1 – Значення матриці U(х,s)
| s1 | s2 | sЗ | s4 | s5 | s6 | s7 | s8 | |
| х1 | 1 | 2 | -2 | 0 | 4 | 6 | 7 | -4 |
| х2 | 0 | 0 | -1 | 0 | 5 | 6 | 1 | 2 |
| хЗ | 4 | 1 | 1 | 2 | 1 | 0 | 2 | З |
| х4 | -6 | 7 | 5 | 5 | 2 | 2 | 0 | З |
| Х5 | -1 | -1 | 0 | 4 | 2 | З | 4 | 5 |
| х6 | -2 | -1 | -2 | 2 | 1 | 0 | З | 4 |
Таблиця 2 – Значення матриці р(х,s)
| s1 | s2 | sЗ | s4 | s5 | s6 | s7 | s8 | |
| х1 | 0 | 0 | 0 | 0.5 | 0 | 0.5 | 0 | 0 |
| х2 | 0 | 0 | 0 | 0 | 0.2 | 0 | 0 | 0.8 |
| хЗ | 0.1 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0.7 |
| х4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Х5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| х6 | 0 | 0.4 | 0 | 0 | 0.6 | 0 | 0 | 0 |
Тоді за методом Байєса – Лапласа – хопт є ![]() шукаємо множину оптимальних рішень:
шукаємо множину оптимальних рішень:
![]()
![]()
![]()
![]()
![]()
![]()
Отже, хопт є {х4}.
Приклад №2:
Початковими даними для прийняття рішення служить матриця ефективностей,
![]() ,
,
тут ![]() - ефективність варіанта,
- ефективність варіанта,
![]()
в ситуации
![]() .
.
Матриця ефективностей:
Таблиця 3 – Початкові дані для прийняття рішень
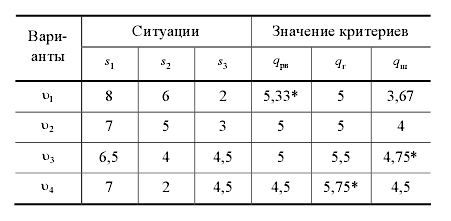
В випадках, коли ймовірності ![]() ситуацій відомі, належне застосування знайшов метод Байєса – Лапласа:
ситуацій відомі, належне застосування знайшов метод Байєса – Лапласа:
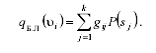
Область застосування методу Байєса – Лапласа:
1) ймовірність ситуацій ![]() відомі і їх можна вважати постійними на період реалізації проекту;
відомі і їх можна вважати постійними на період реалізації проекту;
2) рішення по проектуванню подібних систем приймається і реалізується часто;
З) ризик від неправильно ухваленого рішення не приводить до серйозних наслідків.
Наприклад, нехай матриця в таблиці. 1 доповнена наступною ймовірністю ситуацій
![]()
Отже, тоді
![]()
![]()
![]()
![]()
![]()
Метод Байєса – Лапласа використовується в поєднанні з іншими методами. [5]
Розділ 3. Розробка програми
0 комментариев