ЗАДАЧА №1
Предприятие выпускает четыре вида продукции П1, П2, П3, П4, при ограниченных запасах сырья С1, С2, С3, используемых для производства продукции. Известна прибыль, получаемая от реализации каждого вида продукции. Требуется определить объемы выпуска каждого вида продукции, которые обеспечат предприятию получение наибольшей прибыли при реализации продукции.
Расход сырья на производство единицы продукции, запасы сырья и прибыль, получаемая от реализации единицы продукции, приведены в таблице.
| Виды сырья | Расход сырья | Запасы сырья | |||
| П1 | П2 | П3 | П4 | ||
| С1 | 2 | 0 | 1 | 2 | 800 |
| С2 | 1 | 2 | 0 | 3 | 900 |
| С3 | 2 | 1 | 2 | 3 | 1500 |
| Прибыль | 8 | 6 | 7 | 9 | --- |
Решение
Пусть Х1, Х2, Х3, Х4 – количество единиц выпускаемой продукции П1, П2, П3, П4 соответственно.
Тогда функция прибыли примет вид:
F(х)=8Х1+6Х2+7Х3+9Х4→max
![]() Запишем ограничения по расходу сырья в виде системы неравенств:
Запишем ограничения по расходу сырья в виде системы неравенств:
2Х1+Х3+2Х4≤800
Х1+2Х2+3Х4≤900
2Х1+Х2+2Х3+3Х4≤1500
Х1,2,3≥0
Перейдем от неравенств к равенствам:
![]() 2Х1+Х3+2Х4+Х5=800
2Х1+Х3+2Х4+Х5=800
Х1+2Х2+3Х4+Х6=900
2Х1+Х2+2Х3+3Х4+Х7=1500
Решение будем вести в форме симплекс-таблиц.
| № п/п | Х баз | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Вi | Вi/ аiк |
| 1 | Х5 | 2 | 0 | 1 | 2 | 1 | 0 | 0 | 800 | 800 |
| 2 | Х6 | 1 | 2 | 0 | 3 | 0 | 1 | 0 | 900 | - |
| 3 | Х7 | 2 | 1 | 2 | 3 | 0 | 0 | 1 | 1500 | 750 |
| «0» | F(х) | -8 | -6 | -7 | -9 | 0 | 0 | 0 | 0 | |
| 1 | Х5 | 1 | -0,5 | 0 | 0,5 | 1 | 0 | -0,5 | 50 | -100 |
| 2 | Х6 | 1 | 2 | 0 | 3 | 0 | 1 | 0 | 900 | 450 |
| 3 | Х3 | 1 | 0,5 | 1 | 1,5 | 0 | 0 | 0,5 | 750 | 1500 |
| «0» | F(х) | -1 | -2,5 | 0 | 1,5 | 0 | 0 | 3,5 | 5250 | |
| 1 | Х5 | 1,25 | 0 | 0 | 1,25 | 1 | 0,25 | -0,5 | 275 | |
| 2 | Х2 | 0,5 | 1 | 0 | 1,5 | 0 | 0,5 | 0 | 450 | |
| 3 | Х3 | 0,75 | 0 | 1 | 0,75 | 0 | -0,25 | 0,5 | 525 | |
| «0» | F(х) | 0,25 | 0 | 0 | 5,25 | 0 | 1,25 | 3,5 | 6375 | |
Как видим, в последней строке все числа положительны, следовательно полученный план является оптимальным.
Для получения максимальной прибыли необходимо выпускать 450 ед. продукции П2 и 525 ед. продукции П3. Максимальная прибыль в этом случае составит 6375 ден. ед.
ЗАДАЧА № 2
Имеется 4 поставщика и 4 потребителя. Известны тарифы на перевозку единицы груза от каждого поставщика к каждому потребителю. Найти оптимальный план перевозки грузов от поставщиков к потребителям, обеспечивающий минимальные затраты.
| 1130 1220 | Потребители | ||||
| 320 | 280 | 210 | 320 | ||
| Поставщики | 420 | 5 | 8 | 1 | 5 |
| 180 | 2 | 6 | 5 | 7 | |
| 350 | 7 | 4 | 9 | 8 | |
| 270 | 6 | 2 | 7 | 9 | |
Так как количество груза у поставщиков (1220) превышает требуемое потребителями количество груза (1130) на 1220 – 1130=90 ед., то введем фиктивного потребителя с количеством груза 90 ед. и нулевыми тарифами на перевозку. Первоначальный опорный план составим методом двойного предпочтения, далее будем его улучшать методом потенциалов. В правом верхнем углу указаны тарифы на перевозку, в левом верхнем углу – сумма потенциалов, внизу по центру – количество перевозимого груза.
| 320 | 280 | 210 | 320 | 90 | Ui | |
| 420 | 4 5 | 1 8 | 1 1 210 | 5 5 210 | -3 0 | 0 |
| 180 | 2 2 180 | -1 6 | -1 5 | 3 7 | -5 0 | -2 |
| 350 | 7 7 140 | 4 4 10 | 4 9 | 8 8 110 | 0 0 90 | 3 |
| 270 | 5 6 | 2 2 270 | 2 7 | 6 9 | -2 0 | 1 |
| Vj | 4 | 1 | 1 | 5 | -3 |
В полученном плане перевозок для всех ячеек сумма потенциалов (Ui+ Vj) не превышает тарифы. Следовательно этот план перевозок является оптимальным и его нельзя улучшить.
Минимальные затраты на перевозку составят:
210*1+210*5+180*2+140*7+10*4+110*8+90*0+270*2=4 060 ден. ед.
ЗАДАЧА №3
Требуется расставить 5 рабочих по технологической цепочке так, чтобы время выполнения всего цикла операций было минимальным. Время, затрачиваемое каждым рабочим при выполнении любой операции приведено в таблице.
| 1-я | 2-я | 3-я | 4-я | 5-я | |
| 1-й | 7 | 8 | 6 | 9 | 7 |
| 2-й | 8 | 7 | 9 | 8 | 7 |
| 3-й | 9 | 8 | 6 | 7 | 5 |
| 4-й | 7 | 6 | 8 | 9 | 8 |
| 5-й | 8 | 9 | 5 | 4 | 9 |
Решение
| 1-я | 2-я | 3-я | 4-я | 5-я | |
| 1-й | 7 | 8 | 6 | 9 | 7 |
| 2-й | 8 | 7 | 9 | 8 | 7 |
| 3-й | 9 | 8 | 6 | 7 | 5 |
| 4-й | 7 | 6 | 8 | 9 | 8 |
| 5-й | 8 | 9 | 5 | 4 | 9 |
| qimin | 7 | 6 | 5 | 4 | 5 |
Zmin=4
| 1-я | 2-я | 3-я | 4-я |
| |
| 1-й | 3 | 4 | 2 | 5 | 3 |
| 2-й | 4 | 3 | 5 | 4 | 3 |
| 3-й | 5 | 4 | 2 | 3 | 1 |
| 4-й | 3 | 2 | 4 | 5 | 4 |
| 5-й |
| 5 | 1 | 0 | 5 |
| qimin | 3 | 2 | 2 | 1 |
![]() Zmin=1
Zmin=1
| 1-я | 2-я | 3-я | 4-я | 5-я | |
| 1-й | 2 | 3 | 1 | 5 | 2 |
| 2-й | 3 | 2 | 4 | 4 | 2 |
| 3-й |
| 3 | 1 | 3 | 0 |
| 4-й | 2 | 1 | 3 | 5 | 3 |
| 5-й |
| 5 | 1 | 0 | 5 |
| qimin | 2 | 1 | 1 |
Zmin=1
| 1-я |
|
|
|
| |
| 1-й |
| 2 | 0 | 5 | 2 |
| 2-й | 2 | 1 | 3 | 4 | 2 |
| 3-й |
| 3 | 1 | 3 | 0 |
| 4-й |
| 0 | 2 | 5 | 3 |
| 5-й |
| 5 | 1 | 0 | 5 |
| qimin | 2 | 1 | 1 |
В конечном виде:
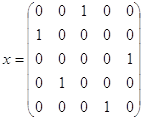
или:
| 1-я | 2-я | 3-я | 4-я | 5-я | |
| 1-й | 7 | 8 | 6 | 9 | 7 |
| 2-й | 8 | 7 | 9 | 8 | 7 |
| 3-й | 9 | 8 | 6 | 7 | 5 |
| 4-й | 7 | 6 | 8 | 9 | 8 |
| 5-й | 8 | 9 | 5 | 4 | 9 |
Время выполнения цикла: 6+8+5+6+4=29 ед. времени.
Похожие работы
... факт; доказательство получается с помощью обратной процедуры.) Принято считать, что последователи Платона изобрели метод доказательства, получивший название «доказательство от противного». Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических ...
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
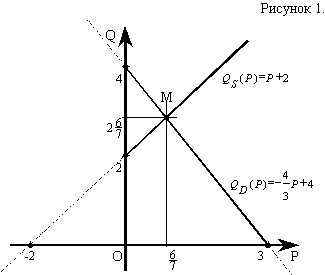
ние месяца, не выходящих в рейс из-за профилактического ремонта автомашин. дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин. Ответ:Каждый водитель из штата гаража в течение месяца может иметь свободных дней. Задание №3. Вопрос №1. Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если , ...
0 комментариев