Навигация
Билет №1
Пусть в обл. P плоскости XOY задана некоторая фун-ия z=f(x;y). Разобъём обл. P на n частичных обл. Рi , где i=1…n, возмём произвольную точку обл. (xI;hI) Î Рi , l - наиболь-ший диаметр чатичных обл.
Построим частичную сумму – сумму Римена.
Определение:
Если существует конечный предел и не зависит от способа делений области на части и от выбора т. (xI;hI) в каждой из частичных областей, то такой предел принято называть двойным интегралом по обл. Р и пишут:
В случае, если фун-ия f > 0 мы приходим к геометрическому смыслу двойного интеграла: днойной интеграл – это объём некоторого цилиндрического тела, сверху ограниченного пов-тью z = (x;y), которая проектируется на плоскость XOY в обл. Р, а образующие параллельны OZ. Площадь обл. Р:
Двойной интеграл от f(x;y) имеет многие св-ва, аналогичные св-ам одномерного интеграла.
Св-ва двойного интеграла:
1.Необходимым условием сущ. Двойного интеграла явл. ограниченность ф-ции f в обл. Р, т.е если сущ. интеграл, то f(x;y) – ограниченная.
2.Всякая непрырывная ф-ция, заданная в обл. Р, интегри-руема.
3.Если ф-ция f(x;y) в обл. Р имеет разрывы на конечном числе непрырывных кривых, принадлежащих этой обл., то f интегрирума по обл. Р.
4.Сумма Дарбу:
Теорема: Для того, чтобы двойной интеграл от ограниченной обл. Р существовал, необходимо и достаточно, чтобы выполнялось равенство:
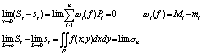
5.Аддетивность двойного интеграла, т.е., если задана обл.Р некоторой непрырывной кривой разбита на две обл-ти Р1иР2 не имеющих общих точек, то, если двойной интеграл по обл. Р существует, то существуют интегралы относительно по двум областям.
6.Линейность:
7.Если f(x;y) £ g(x;y) для "(x;y)ÎP и ф-ции f и g интегрируемы, то соответственно справедливо неравенство:
9.Если f(x;y) удовлетворяет нер-вам m £ f(x;y) £ M, то справедливо следующее неравенство:
10.Для двойного интеграла имеет место теорема о среднем: если z = f(x;y) – ф-ция, заданая в обл. Р и такая, что во всех точках этой области выполняется нер-во m £ f(x;y) £ M, где
то существует число m такое, что справедливо равенство:
В случае непрырывности ф-ции:
Вопрос №3
Пусть в плоскости XOY задана плоскость Д, ограничен-ная следующими кривыми: y=j1(x) a £ x £ a – снизу;
y=j2(x) a £ x £ b – сверху; x = a – слева; x = b – справа;
Тогда имеет место следующая теорема.
Теорема: Если функция f(x;y) задана в области Д такова, что существует двойной интеграл
для любого фиксированного xÎ [a ; b] существует одно- мерный интеграл
то тогда существует повторный интеграл
Доказательство:
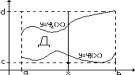
Обозначим c=inf j1(x) a £ x £ b; d=max j1(x) a £ x £ b и рассмотрим прямоугольник R=[a,b;c,d]ÉД. P=RД (раз- ность множеств). Построим вспомогательную функцию
Рассмотрим
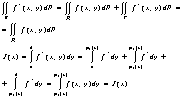
Получаем следующее равенство:
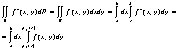
Замечание: Пусть теперь область Д ограничена следующими линиями:
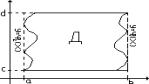
x=y1(y) c £ y £ d – слева; x=y2(y) c £ y £ d – справа;
x = c – сверху; x = d – снизу. И пусть
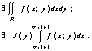
Тогда аналогично предыдущему можно показать, что существует повторный интеграл и
Если же функция f(x;y) такова, что существует двойной интеграл, существует оба повторных, то одновременно имеют место формулы (1) и (2) и можно пользоваться любой из них.Вопрос №5
Формула Грина.
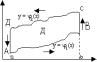
Теорема: Пусть задана область Д огран. след. кривыми:
y=j1(x) a £ x £ b
y=j2(x) a £ x £ b
x=a , x=b, где ф-ции j1 и j2 непрер. на (a,b). Пусть в этой области задаётся функция P(x,y) – непрер. и имеющая непрер. частную производную: 
, тогда имеет место след. равенство:
Доказательство:
Рассмотрим двойной интеграл, стоящий справа в формуле(1). Т.к. под интегралом стоит непрер. функция, то такой двойной интеграл существует, также существует одномерный интеграл
и его можно вычислить через повторный:
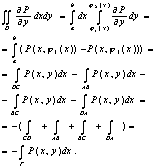
Теорема: Пусть задана область Д огран.:
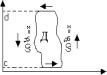
y=j1(x) с £ x £ d
y=j2(x) c £ x £ d
x=c , x=d. И пусть в этой области задаётся функция Q(x,y) – непрер. и имеющая непрер. частную производную: 
, тогда имеет место след. равенство:
Cкладываем формулы (1) и (2) и получаем следующую формулу Грина для области Д:
D P(x,y), Q(x,y) 
, 
Вычисление площадей через крив интеграл
Применим ф. Грина, т.е. выразим его через криволинейный интеграл по границе области.
1. Q = x P = 0
2. Q = 0 P = -y
Суммируем 1 и 2 :
Пример: Вычислить площадь эллипса
.
Сделаем замену переменных
Похожие работы
... данным, n=20 Найти матрицу А-1, обратную к матрице А и с ее помощью решить систему А =, где , = , = . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИКА (углубленный курс) Билет № 12 Что называется характеристическим уравнением дифференциального уравнения II порядка с постоянными коэффициентами? По какой ...
... быть выведены на печать. На экране рисунки могут быть статическими (неподвижными) или динамическими (движущимися). В последнее время машинная графика выделилась в самостоятельный раздел информатики с многочисленными приложениями. Средствами машинной графики создается не только печатная продукция, но и рекламные ролики на телевидении, мультфильмы. Объясним, как кодируется изображение в памяти ...
... уроки сказки, веселые задачи в стихах, математические загадки, сказочные задачи, математические сказки, задачи занимательного характера, головоломки, кроссворды и логические задачи способствуют активизации мыслительной деятельности учащихся на уроках математики, подтвердилась. Для себя лично я усвоила правило: "Не бери игру на урок, для того чтобы развлечься. Все на уроке должно быть логически ...
... вероятностей совместимых событий; формулы: полной вероятности, Бейеса (Байеса). Одной из форм дифференцированного обучения по курсу теории вероятностей может являться факультативный курс. 2. Разработка программы факультативного курса по теории вероятностей в курсе математики 8 класса 2.1 Основные понятия о факультативном курсе Возможность 1-2 часа в неделю дополнительно работать со ...
0 комментариев